Урок по геометрии "Действия над векторами" 10 класс

Урок №36

Тема программы: Раздел 5. Координаты вектора в пространстве – 8 часов.

Тема урока: Действия над векторами

Содержание: 5.2 Прямоугольные координаты на плоскости и в пространстве. Действие над векторами, заданными координатами. Формулы для вычисления длины вектора, угла между векторами, расстояние между двумя точками.

 Цель урока: Формировать у учащихся знания и умение по теме вектора. Расширить знания о векторах:  определить что такое вектор в пространстве и рассмотреть связанные с ним понятия- абсолютной величины, направления, равенства векторов, вывести формулу  координат вектора в пространстве. Научить применять ее к решению задач.

Тип урока: Совершенствования зун.

Методы ведения: Комбинированный урок.

Оборудование урока  формулы, справочный материал

ХОД УРОКА:

Организационный момент – 1 – 2 мин.

1.      Приветствие учащихся.

2.      Отметить отсутствующих.

II.      Опрос по домашнему заданию

1.Определение вектора.

2. Нулевой вектор.

3. Коллениарные вектора.

4. Комплонарные вектора.

5. Абсалютная величина вектора.

6. Длина вектора.

III.   Объяснение нового материала. Краткий конспект.

Длина (модуль) вектора  обозначается  и определяется по формуле:

Вектор , начало которого находится в начале координат, а конец – в точке  М(x;y;z) называют радиусом – вектором точки М и обозначают  (М) или просто . Так как его координаты совпадают с координатами точки М, то его разложение по ортам имеет вид:

Вектор , имеющий начало в точке А( х₁; y_1; z₁) и конец в точке В(х₂; y_2; z₂) может быть записан в виде = -, где - радиус- вектор точки А, - радиус – вектор точки В.Поэтому разложение векторапо ортам имеет вид:

Его длина совпадает с расстоянием между точками А и В:

Координаты вектора

Числа x, y и z называются координатами вектора  в данном базисе. В этом случае пишут:

Действия над векторами, заданными своими координатами

IV. Закрепление нового материала:

Задача № 1

Точка К – середина отрезка АВ. Найдите длину отрезка АВ, если известны координаты точек А и К.

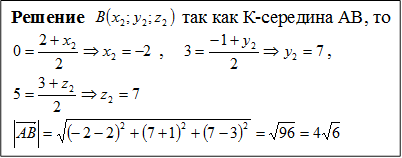
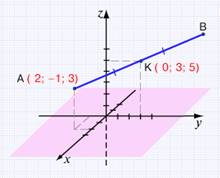
 Задача № 2

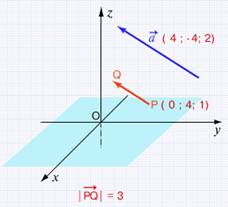
От точки Р, координаты которой известны, отложили вектор с концом в точке Q, длиной 3 и сонаправленный вектору с координатами (4; -4; 2). Найдите координаты точки Q.

Задача № 3

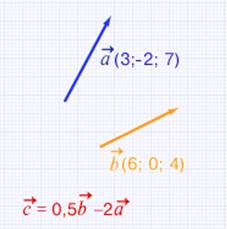
Даны координаты двух векторов. Найдите длину вектора, который является линейной комбинацией исходных векторов.

Задача №4  Найти длину вектора , если  и

Решение:

 и

Задача №5  Найти длину вектора , если  и

Решение:

Пусть , тогда  и

Задача №6.  Найти длину вектора , если  и

Решение:  и , пусть , тогда

Задание на дом §24-25 №201

Литература:  Ж. Кайдасов, В. Гусев, А Кагазбаева Геометрия 10, 11 классы. Дидактический материал по геометрии для 10, 11 классов.

Скачано с www.znanio.ru