Урок по теме "Этот удивительный мир симметрии"

Урок по теме "Этот удивительный мир симметрии"

 

Цели:

1. Развитие пространственного воображения.

2. а) Изучение многообразных проявлений симметрии в окружающем мире;

    б) Понимание важной, исключительной роли принципа симметрии в научном познании мира и в человеческом творчестве.

3. Воспитание профессионально значимых качеств личности.

 

Оборудование: мультимедиа, ЦОР (презентация к уроку), плакаты,  рисунки, многогранники, плоские фигуры.

 

На доске: “Симметрия является той идеей, посредством которой, человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство”

 

Ход урока:

 

Урок проводится в форме конференции, выступают учащиеся с заранее подготовленными материалами по выбранной ими теме, направлению.

 

1. Организационный момент.

 

Ведущий – преподаватель математики: « Симметрия… есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство». Эти слова принадлежат известному математику Герману Вейлю. С симметрией мы встречаемся везде: в природе, технике, искусстве, науке. Отметим, например, симметрию, свойственную бабочке и кленовому листу, симметрию форм автомобиля и самолета, симметрию в ритмическом построении стихотворения и музыкальной фразы, симметрию атомной структуры молекул и кристаллов.

Сегодня на этом уроке ознакомимся с симметрией в биологии, физике, математике, искусстве, музыке и музыкальных произведениях.

Термин “симметрия” по-гречески означает “соразмерность, пропорциональность, одинаковость в расположении частей”.

 

2. Ход конференции.

 

I. Симметрия в пространстве.

 

ВЕДУЩИЙ: Что же скажет о симметрии математик.

 

 учащийся - математик:

В   планиметрии   мы   рассматривали   фигуры, симметричные относительно   точки   и   прямой.   В   стереометрии рассматривают симметрию относительно точки, прямой и плоскости.

 

1. Точки    А  и   А₁ , называются

симметричными относительно точки О (центр симметрии), если О - середина отрезка АА₁ . О считается симметричной самой себе.

                                                                                                                             А₁

                                                                                 О

                                                         

                                                          А

 

2.  Точки  А   и   А₁   называются  симметричными  относительно прямой   а   (ось симметрии),   если   прямая проходит  через  середину  отрезка   АА₁   и перпендикулярна   этому   отрезку.    Каждая   точка   прямой   а   считается   симметричной  самой   себе.  

                                                      а

                 А                                                                       А₁

 

3. Ежедневно каждый из нас по несколько раз в день видит отражение в зеркале. Это настолько обычно, что мы не удивляемся, не задаем вопросов, не делаем открытий. И только философы и математики не теряют способности удивляться. Немецкий философ Иммануил Кант говорил о зеркальном отражении так: «Что может быть более похоже на мою руку или мое ухо, чем их собственное отражение в зеркале? И все же руку, которую я вижу в зеркале, нельзя поставить на место постоянной руки ...»

Это и есть симметрия относительно плоскости.

Точки А и А₁, называются симметричными относительно плоскости  α (плоскость симметрии), если плоскость α проходит через середину отрезка АА₁ и перпендикулярна этому отрезку. Каждая точка плоскости α  считается симметричной самой себе.

 

 

                       А                                                                                                                                           А₁

                                                               α    

                                             

4. Введем понятия центра, оси и плоскости симметрии фигуры.

Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией.

Примером  симметричных объектов являются: а) одномерный объект (О - центр симметрии) рис 1;  б) двухмерный объект (I – ось симметрии) рис.2.;  в) трехмерный объект (a - плоскость симметрии) рис 3.

 

 

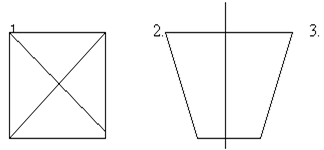
 Осей и плоскостей симметрии может быть несколько. Бесконечное число плоскостей симметрии имеет шар, круговой цилиндр, круговой конус, и т.д.

 

 

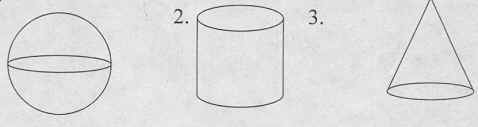
Правильный шестиугольник имеет 6 осей симметрии, круг - бесконечное множество осей симметрии.

 

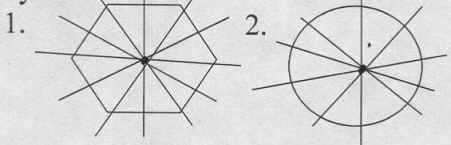
И вот и домашнее задание, найти фигуры имеющие несколько осей и плоскостей симметрии.

 

Примечание: Условия построения симметричных фигур объясняется и записывается с целью правильного построения более сложных фигур.

II. Симметрия в природе.

 учащийся - биолог:

«Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всем в жизни симметрия?» - задавал вопросы Николенька Иртеньев из «Отрочества» Л. Толстого.

Почему же в природе царит симметрия? Почему симметрично все живое от микроорганизмов до человека?

Господство симметрии в природе объясняется силой тяготения, действующей во всей Вселенной. Действием тяготения или отсутствием такового объясняется то, что и космические тела, плавающие во Вселенной, и микроорганизмы, взвешенные в воде, обладают высшей формой симметрии - сферической (при любом повороте относительно центра фигура совпадает сама с собой). Все организмы, растущие в прикрепленном состоянии (деревья) или живущие на дне океана (морские звезды), т.е. организмы, для которых направление силы тяжести является решающим, имеют ось симметрии. Для животных, способных передвигаться в воде, воздухе или по земле, кроме направления силы тяжести, важным оказывается и направление движения животного. Такие животные имеют плоскость симметрии. Биологи эту плоскость симметрии называют билатеральной, а тип симметрии - зеркальным.

Характерная для растений симметрия конуса хорошо видна на примере фактически любого дерева (рис.1).

Дерево при помощи корневой системы поглощает влагу и питательные вещества из почвы, т.е. снизу, а остальные жизненно важные функции выполняется кроной, т.е. наверху.

Вертикальная ориентация оси корпуса характеризует симметрию дерева. Ярко выраженной симметрией обладают листья, цветы, ветви, плоды( рис. 2). Для цветов характерна поворотная симметрия. На рисунке 3(а) цветок зверобоя имеет центральную симметрию. Часто центральная симметрия цветов сочетается с зеркальной симметрией (рис.3 б)

рис. 3(а)

рис. 3(б)

На рисунке 4 веточка акации имеет зеркальную и осевую симметрию. Веточка боярышника на рисунке 5 обладает скользящей осью симметрии.

Поворотная (центральная)симметрия встречается и в живом мире. Примером могут служить морская звезда и панцирь морского ежа (рис 6а,б)

 

Зеркальная (билатеральная – это слово чаще встречается в биологии) симметрия , характерна всем представителям животного мира. Эта симметрия хорошо видна у левого и правого крыльев бабочки и проявляется здесь с почти математической строгостью (рис. 7)

Можно сказать, что каждое животное состоит из двух энатиморов - правой и левой половины (еще несколько слайдов - картинок).

Отметим, наконец, билатеральную симметрию человеческого тела (речь идет о внешнем облике и строении скелета). Эта симметрия всегда являлась и является основным источником нашего эстетического восхищения хорошо сложенным человеческим телом.

 

ВЫВОД: Симметрия ограничивает многообразие структур, которые могут существовать в природе.

 

ВЕДУЩИЙ: Дальше поговорим о симметрии в неживой природе. Наверное, не случайно безжизненный замок Снежной королевы из известной сказки Андерсена часто изображают как высшей степени симметричное сооружение.

 

 учащийся - физик: Камни лежащие у подножия горы весьма беспорядочны; однако каждый камень является огромной колонией кристаллов, которые представляют собой в высшей степени симметричные постройки из атомов и молекул. Именно кристаллы вносят в мир неживой природы очарование симметрии. Как из вас не любовался снежинками?

Каждая снежинка – это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией. 

Все твердые тела состоят из кристаллов. На рисунке представлены кристаллы топаза, берилла, дымчатого кварца.

Симметрия внешней формы кристаллов хорошо видна на рисунке, где показаны кристаллы каменной соли(а), кварца (б), арагонита ( в).

 

А на этом рисунке изображены три формы кристаллов алмаза: (а) октаэдр, (б) ромбический додекаэдр, (в) гексагональной октаэдр.

 

 

Вывод: Симметрия внешней формы кристалла является следствием его внутренней симметрии – упорядоченного взаимного расположения в пространстве атомов (молекул).

Иначе говоря, симметрия кристалла связана с существованием пространственной решетки из атомов так называемой кристаллической решетки.

 

ІII. Симметрия в искусстве: архитектуре, скульптуре, живописи.

 

ВЕДУЩИЙ:

Если мы сказали, что симметрия в живой и неживой природе проявляется с математической строгостью, как же человек может это изобразить. Слово художнику.

 

 учащийся - художник: Рассказ о симметрии в живописи и архитектуре.

 

    

Рис. 3 Евхаристия. Мозаика апсиды собора Св. Софии в Киеве.

 

  

 Рис. 7 - 8.

На рисунках 1-8 хорошо видна симметрия.

ПРИМЕЧАНИЕ: учащийся объясняет, как определить симметрию, в живописи, скульптуре и архитектуре.

 

ВЫВОД: Получается, что всякий раз, когда мы, говорим о гармонии, красоте, эмоциональности воздействуя, мы тем самым касаемся симметрии.

 

ВЕДУЩИЙ: Звучит музыка…  Где же симметрия в музыке. Слово музыканту.

 

5 учащийся - музыкант: Душа музыки, ритм, состоит в правильном периодическом повторении частей музыкального произведения. Правильное повторение одинаковых частей в целом и составляет сущность музыки. Мы с большим правом можем приложить к музыкальному произведению понятие симметрии, что это произведение записывается при помощи нот. Самое непосредственное отношение имеет к симметрии композиция. Великий немецкий поэт И.В. Гете утверждал, что « Всякая композиция основана на скрытой симметрии. Владеть законами композиции – это значит владеть законами симметрии”.

В каждой песне чередуется куплет и припев.

 Симметрию можно увидеть в стихотворениях – это чередование рифм, ударных слогов, т.е. ритмичность.

Например:   А.С. Пушкин.

В тот год осенняя погода
Стояла долго на дворе
Зимы ждала, ждала природа
Снег выпал только в январе.

Чередование рифм и чтение по интонации дает чувствовать прелесть (симметрии) пушкинского стихотворения.

 

6 учащийся – о симметрии в профессии помощник машиниста локомотива (электровоза).

 

Идеально симметрична колесная пара вагона. Во-первых, она имеет центральную осевую симметрию. Даже незначительное отклонение колес от круглости (овальность) вызывает повышенный износ колес и рельсов, биение колесной пары (как следствие – повреждения вагона и груза), увеличивает трение качения. Овальность определяется замерами диаметра в различных направлениях. У круглого колеса все диаметры, измеренные с высокой точностью, должны быть равны.

 

Колесная пара симметрична относительно своей центральной части. Расстояния от торца оси до внутренней грани колеса жестко нормируются. Разница размеров l допускается не более 3 мм. В противном случае будет наблюдаться односторонний износ гребней и повышенное сопротивление движению поезда.

 

Интересный пример симметрии можно привести, рассматривая косозубую тяговую передачу грузового электровоза. Зубчатая передача с наклонными зубьями лучше работает: мягко, бесшумно, меньше изнашивается. Но она имеет серьезный недостаток – зубья ведущей шестерни, воздействуя на наклонные зубья ведомого зубчатого колеса, стремятся сдвинуть его в осевом направлении. Симметрия позволяет решить эту проблему. Зубчатые колеса располагаются на оси колесной пары электровоза симметрично относительно середины оси, причем таким образом, что зубья наклонены в разные стороны. В этом случае составляющие силы, действующие в осевом направлении, компенсируются и передача работает без упорных подшипников.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Еще один пример симметрии – так называемая развеска электровоза. Оборудование внутри кузова располагают так,  чтобы оно по весу располагалось симметрично относительно продольной и поперечных осей. В этом случае обеспечивается равномерная нагрузка на все колесные пары.

 

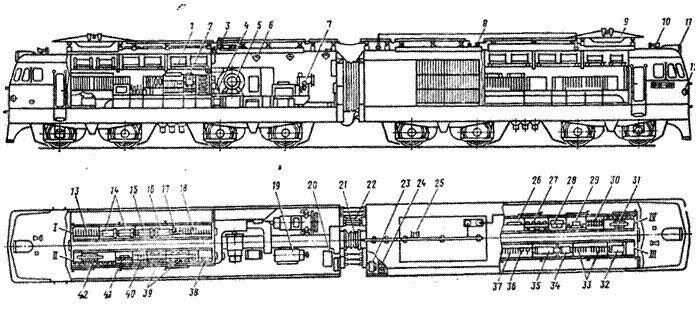
ВЕДУЩИЙ: Мы остановились только на симметрии, но мне хочется сказать несколько слов об асимметрии. Проблему симметрия – асимметрия следует понимать глубже. Симметрия и асимметрия настолько взаимосвязаны, что должны рассматриваться как две стороны единого понятия. Чем удачнее решает архитектор, композитор, поэт соотношение между симметрией и асимметрией, тем выше художественная ценность создаваемого произведения искусства. Но пусть эта тема будет для вас темой реферата.

 

3. Итоги урока. Рефлексия.

 

4. Домашнее задание.

 

Приложение 1.

 

Вопросы теста.

 

1. Сколько центров симметрии имеет параллелепипед?
2. Сколько центров симметрии имеет правильная треугольная призма?
3. Сколько центров симметрии имеет двугранный угол?
4. Сколько центров симметрии имеет отрезок?
5. Сколько осей симметрии имеет отрезок?
6. Сколько осей симметрии имеет правильный треугольник?
7. Сколько осей симметрии имеет куб?
8. Сколько плоскостей симметрии имеет правильная четырехугольная призма, отличная от куба?
9.  Сколько плоскостей симметрии имеет правильная четырехугольная пирамида?
10.  Сколько плоскостей симметрии имеет правильная треугольная пирамида?
11.  Какие точки называются симметричными относительно точки?
12.  Какие точки называются симметричными относительно прямой?
13.  Какие точки называются симметричными относительно плоскости?
14.  Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.
15.  Если фигура имеет центр (ось, плоскость) симметрии, то она обладает центральной (осевой, зеркальной) симметрией.