
Урок по теме "Осевая и центральная симметрия"
Тип урока: Изложение нового материала.
Цели урока:
Оборудование: мультимедийная аппаратура, раздаточный материал: задания с лабораторной работой, карточки с исследовательскими задачами, презентация.
Учащиеся 9 класса разбиваются на группы по 4-5 чел.
Ход урока.
Сложить из букв слово Д В И Ж Е Н И Е.
движение .
(Вывешивается плакат на магнитную доску.)
Эпиграф урока:
«Природа не знает остановки в своем движении и казнит всякую бездеятельность».
Иоганн Вольфганг Гёте, немецкий прозаик (Слайд 1)
Ребята! Чем предстоит заниматься на уроке?
Запишите число и тему урока «Понятие движения». (Слайд 2)
2 Изучение нового материала
Задание 1. У вас на столах лежат картинки (Слайд 3). Ваша задача распределить их в три группы по определенным признакам. На выполнение задания вам 2 минуты.
Вопросы к заданию:
По какому принципу вы распределяли картинки?
Что помогло выявить эту закономерность?
В чем различия между группами рисунков?
(Как правило, дети раскладывают картинки не следуя принципам симметричности. К концу урока они смогут разложить картинки учитывая вид симметрии.)
Вы правильно классифицировали картинки. В конце урока мы попытаемся расположить картинки по другому принципу, с точки зрения математики.
Симметрия - в переводе с греческого означает "одинаковость в расположении частей, пропорциональность", "гармония", "красота".
Кто не любовался симметричностью творений природы: листьями, цветами, птицами, животными; или творениями человека: зданиями, техникой, - всем тем, что нас с детства окружает, тем, что стремится к красоте и гармонии.
Герман Вейль - немецкий математик сформулировал определение симметрии сравнительно недавно - в начале ХХ века. И наша с вами задача попробовать повторить его открытие, самостоятельно вывести определение осевой симметрии и центральной симметрии. На уроке мы рассмотрим осевую и центральную симметрию, а с зеркальной симметрией более подробно вы познакомитесь в старших классах.
У вас на столах лежат листы-задания к лабораторной работе №1. В результате выполнения работы вы должны сформулировать определение точек симметричных относительно прямой. На выполнение работы вам отводится 5 минут.
Лабораторная работа №1 (Слайд 4)
1) Возьмите лист белой бумаги, согните его пополам.
2) Капните на него каплю краски, (пусть это будет точка А) , а затем разогните.
3) На другой стороне листа вы получили такую же точку (пусть это будет точка А1).
4) Соедините А и А1 отрезком.
5) Измерьте расстояние от А и от А1 до линии сгиба.
Расстояние от А до линии сгиба равно _______________________
Расстояние от А1 до линии сгиба равно ______________________
6) Сравните эти расстояния. Они ____________________
7) Определение:
Две точки А и А1 называются симметричными относительно прямой, если эта прямая проходит через____________________ отрезка АА1 и ______________________ к нему.
Запишите определение в тетрадь.
Определение 1: Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
Задание 2. Перенесите рисунок себе в тетрадь (слайд 5) и постройте точку К1, симметричную точке К относительно прямой т.
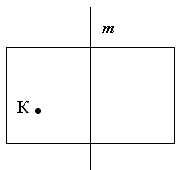
Задание 3
Двое у доски, остальные в тетрадях.
1) Постройте фигуру, симметричную данной относительно прямой l. (Слайд 6)
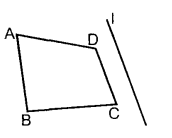
Самопроверка по образцу на доске. Оценивание работавших у доски.
Вопросы после выполнения задания:
Какие условия должны выполняться, чтобы точка А1 была симметричной точке А относительно: прямой l? (Симметрия Слайды 7-17)
Лабораторная работа №2 ( Слайд 18)
1. Постройте параллелограмм АВСD.
2. Проведите диагонали параллелограмма.
3. Отметьте их точку пересечения О.
4. Отметьте на стороне АВ произвольную точку М и постройте точку М1, симметричную точке М относительно центра О.
5. Отметьте на диагонали АС точку К, отличную от точки О и постройте точку К1 симметричную точке К относительно центра О.
6. Сделайте вывод: если точка принадлежит параллелограмму, то где находится симметричная ей точка?
7. Определение
Фигура называется симметричной относительно центра, если для каждой точки фигуры_______________ей точка также ________ этой фигуре.
Проверим по слайду правильность ваших построений
Вопросы: Обсудите в группах и сформулируйте, какая фигура называется симметричной относительно центра?
Определение 4: Фигура называется симметричной относительно центра, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре. (Слайд 20)
Задание 4 Постройте
фигуру, симметричную данной относительно точки О. 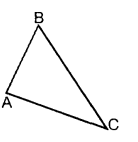
. О
Самопроверка по образцу на доске. Оценивание работавших у доски.
Вопросы после выполнения задания:
Какие условия должны выполняться, чтобы точка А1 была симметричной точке А относительно: точки О?
Симметрия присутствует не только в геометрии и в алгебре. Я хочу вам предложить еще несколько прекраснейших творений природы и человека. (Показ видео.)
А теперь давайте вернемся к началу урока. Вы должны сгруппировать картинки уже с математической точки зрения?
Сравните со слайдами (слайды 25-26), все ли вы выполнили верно? Поздравляю вас с успешным выполнением поставленной задачи.
Ребята, давайте подведём итог.
Что такое движение плоскости?
Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.
Какие виды движений мы изучили?
§ осевая симметрия
§ центральная симметрия
- Каким общим свойством обладают осевая и центральная симметрии?
Наводящие вопросы:
- В какую фигуру отобразился четырехугольник ABCD при осевой симметрии?
- В какую фигуру отобразился треугольник АВС при центральной симметрии?
- Сохранилось ли расстояние между двумя точками при осевой симметрии? При центральной симметрии?
Итак, общее свойство осевой и центральной симметрии?
сохраняются расстояния
Домашнее задание: п. 117, 118, № 1152.
Спасибо за урок, мне приятно было с вами работать.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.