Урок_1_Квадратное неравенство_Методические рекомендации (2)

Методические рекомендации к уроку №1

темы/подраздела «Квадратное неравенство»

раздела «Неравенства»

Тема урока: Решение квадратных неравенств

Цель обучения:

8.2.2.8 решать квадратные неравенства

На изучение способов решения квадратных неравенств выделено 5 уроков. На первом уроке будет рассмотрена схема решения неравенств в зависимости от знака дискриминанта.

Теоретический материал

Неравенство, левая часть которого многочлен второй степени, а правая часть равна нулю, называют квадратным неравенством.

Неравенства вида  и  называются строгими, а неравенства вида  и  нестрогими.

Так как неравенства  и  имеют одинаковые решения (т.е. равносильны), то можно рассмотреть решение квадратных неравенств только для случая .

Решение квадратных неравенств зависит от знака дискриминанта.

1. Пусть D < 0.

Квадратный трехчлен  можно записать так: .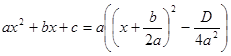

Так как   при любых х,  (т.к. D < 0) и , значение выражения  всегда положительно, т.е. неравенство  верно всегда, а неравенства  и  не выполняются ни при каких х.

2. Пусть D = 0.

Тогда равенство 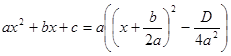 примет вид . Это выражение при  принимает неотрицательные значения. Следовательно, неравенство  верно всегда, неравенство  не выполняются ни при каких х.

3. Пусть D > 0.

Тогда квадратный трехчлен  можно записать как произведение , где  и  - корни уравнения . Положим для определенности, что .

При  оба множителя в произведении  отрицательны, поэтому выражение  принимает положительные значения.

При  множитель  положителен, а множитель  отрицателен, значит выражение  принимает отрицательные значения.

Таким образом, при  и D > 0 решение неравенства  является объединением промежутков  и , а решение неравенства  - промежуток .

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

В начале урока предлагается несколько заданий на повторение, которые помогут учащимся лучше понять решение квадратных неравенств. Изучение нового материала основано на обсуждении возможных значений квадратного трехчлена в зависимости от знака дискриминанта. Результатом обсуждения будут схемы решения неравенств, которые учащиеся будут применять при выполнении заданий. Этот подход предложен в учебнике Алгебра 8 Виленкина Н.Я.

Для закрепления материала учащиеся решат несколько неравенств, соответствующих разным случаям для знака дискриминанта. Решения предлагается обсуждать всем классом, так как это первый урок раздела и учащимся нужно учиться корректно использовать предметную терминологию.

Ответы и решения

Решите неравенства:

а)

Решение.

Уравнение имеет два корня  и , значит решение неравенства – промежуток .

б) .

Решение.

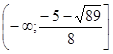Уравнение имеет два корня  и , значит решение неравенства – объединение промежутков  и .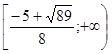

в)

Решение.

Решением неравенства  является множество всех действительных чисел.

г)

Решение.

, значит уравнение имеет единственный корень . Поэтому решением неравенства будет единственное число .

д) .

Решение.

Умножив обе части на -1 получим неравенства с положительным старшим коэффициентом .

, значит неравенству не удовлетворяет ни одно значение х, т.е. .

Дополнительные разноуровневые задания

Найдите значения х, при которых имеет смысл выражение:

а) ;

б) ;

в) ;

г) .

Список полезных ссылок и литературы

1.      Виленкин Н.Я., Виленкин А.Н., Сурвилло Г.С. и др. Алгебра: учеб. для 8 кл.  с углубленным изучением математики.  – М.: Просвещение, 2006. 303 с. : ил.

2.       Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений.  – М.: Мнемозина, 2010

3.      Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре, 8-9 классы.  – М.: Просвещение, 2009. 301 с.: ил.

4.