Урок_1_Приложение 1_О применении свойств квадратичной функции

Параболические кривые используются при проектировании систем освещения, телескопов и радиолокационных антенн, главным образом из-за отражающего свойства, которое вы можете видеть на рисунке справа. Фонари и автомобильные фары просто отражают этот процесс. Источник света находится в фокусе параболического зеркала (точке F). Световые лучи попадают в зеркало с углом падения, равным углу отражения, и каждый луч отражается вдоль пути, параллельного оси. В результате получается световой поток параллельных лучей.

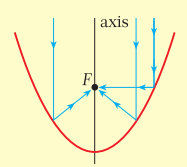
Параболические зеркала, улавливающие солнечный свет, используются для разогревания продуктов, выработки электричества, в металлообработке и при получении водорода. Самый крупный из таких объектов расположен в деревеньке Одейо во французских Пиренеях: 8-этажный массив включает 10 тыс. небольших зеркал, вместе создающих в фокальной точке температуру в 3 тыс. градусов по Цельсию.

Многие процессы в физике, биологии, строительстве, архитектуре, технике протекают по свойствам квадратичной функции. Например, если предмет брошен вертикально вверх или вертикально вниз, то зависимость высоты h, на которой находится предмет в момент времени t является квадратичной функцией и задается формулой , где  - начальная скорость предмета,  - высота, с которой прошен предмет, g – ускорение свободного падения (с этим понятием вы более подробно познакомитесь на уроках физики), .

На этом факте основан один из способов измерения глубины пещер, колодцев, шахт и т.д. Сверху сбрасывают камень и с максимально возможной точностью засекают время, через которое будет услышан звук от его удара о землю. Зависимость глубины h от времени полета камня задается формулой   (объясните, как получена эта формула). Остается подставить в эту формулу время, которое пролетел камень, и вычислить глубину объекта.

 Траектория движения некоторых объектов является параболой. Дельфины поднимаются над водой по траектории, похожей на параболу. Многие животные прыгают по той же траектории. Снаряд, выпущенный из пушки под углом, струя воды в фонтане также перемещаются по параболической траектории.

Скачано с www.znanio.ru