Урок_1_Решение квадратных уравнений с модулем_Методические рекомендации (1)

Методические рекомендации к уроку №1 темы/подраздела

«Решение уравнений»

раздела «Квадратные уравнения»

Тема урока: Решение квадратных уравнений, содержащих знак модуля

Цель обучения:

8.2.2.5

решать уравнения вида |ax²+bx|+c=0; ax²+b|x|+c=0

На изучение подраздела «Решение уравнений» отведено 8 часов. Два первых урока посвящены решению квадратных уравнений, содержащих знак модуля. Также в данном подразделе будут рассмотрены дробно-рациональные уравнения и другие уравнения, сводящиеся к квадратным.

Теоретический материал

Определение модуля числа а:

Алгоритм решения уравнения вида ax²+b|x|+c=0

1. Избавиться от знака модуля, для этого записать совокупность систем уравнений и неравенств:

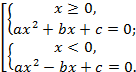
2. Решить полученные квадратные уравнения:

3. Проверить корни (т.е. решить системы уравнений и неравенств).

4. Записать ответ.

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

В начале урока предусмотрено выполнение устных тестовых заданий с целью повторения ранее изученного материала. Способ организации деятельности учащихся на данном этапе будет способствовать развитию быстроты мышления. Хотя некоторые вопросы можно отнести к вопросам низкого порядка, все же знание этих фактов необходимо для успешного усвоения темы рока. Учащиеся используют карточки с буквами для демонстрации выбранного ответа. Это будет способствовать вовлечению в работу всего класса, а также поможет учителю оперативно оценить уровень владения учащихся тем или иным материалом. Вопросы в начале теста призваны напомнить учащимся о возможности применения различных способов решения полных и неполных квадратных уравнений. В течении урока учителю следует поощрять применение учащимися этих способов. Последнее задание устного счета необходимо для повторения понятия модуля и его свойств.

При изучении нового материала целесообразно дать учащимся некоторое время для обдумывания способа решения квадратного уравнения, содержащего модуль. Это поможет учащимся «надстроить» новые знания на уже имеющийся фундамент в процессе самостоятельного создания алгоритма решения таких уравнений.

На этапе первичного закрепления материала предлагается работа в парах, чтобы учащиеся могли оказать друг другу поддержку в формировании навыка применения алгоритма. Возможность проговаривания этапов решения уравнений поможет лучше понять и усвоить различные нюансы. Учитель будет слушать обсуждения учащихся, помогать в улучшении навыка применения математической речи.

В конце урока предложена самостоятельная работа учащихся. Учитель может обходить класс и предоставлять устную обратную связь отдельным учащимся, чтобы своевременно устранить возникающие проблемы. Следует обращать внимание на запись решения. Также можно использовать образцы готовых решений, представленные ниже, для организации самооценивания. В этом случае решения нужно распечатать и разместить на разных стенах классной комнаты. Учащиеся после выполнения соответствующего задания смогут подойти и проверить свое решение.

Для домашней работы учащимся даны не только задания на закрепление изученного на уроке материала, но и задания на повторение действий над алгебраическими дробями, так как на следующих уроках учащиеся будут изучать способы решения дробно-рациональных уравнений.

Вопросы для рефлексии учащиеся могут обсудить в парах. Также следует обратить внимание учащихся на пути решения возникших трудностей.

Ответы и решения

Работа в парах

Решите уравнения:

а)

Решение.

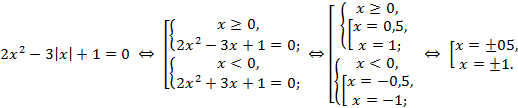
б) .

Решение.

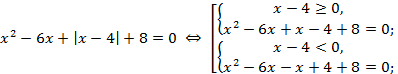
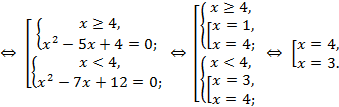
Самостоятельная работа

Решите уравнения:

а)

Решение.

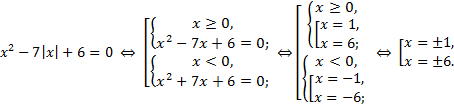
б)

Решение.

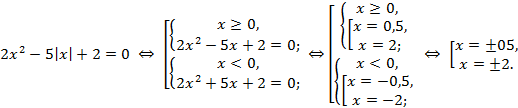
в)

Решение.

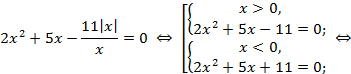
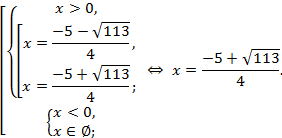
г) .

Решение.

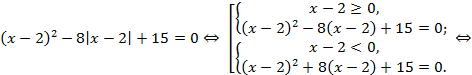
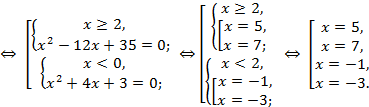
Список полезных ссылок и литературы

1.                   Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 8 класс : учеб. для учащихся общеобразоват. учреждений  – М. : Мнемозина, 2010. – 384 с. : ил.

2.                   Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Дидактические материалы. 8 класс: пособие для шк. с углубл. изучением математики – М. : Мнемозина, 2010. – 157 с. : ил.

3.                   Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре, 8-9 классы.  – М.: Просвещение, 2009

4.                   Феоктистов И.Е. Алгебра. 8 класс.  Дидактические материалы. Методические рекомендации. – М.: Мнемозина, 2012. – 173 с. : ил.

5.