Поделиться
Урок_2_Решение квадратных уравнений с модулем_Методические рекомендации (1).docx
Методические рекомендации к уроку №2 темы/подраздела
«Решение уравнений»
раздела «Квадратные уравнения»
Тема урока: Решение квадратных уравнений, содержащих знак модуля
Цель обучения:
8.2.2.5
решать уравнения вида |ax2+bx|+c=0; ax2+b|x|+c=0
На изучение подраздела «Решение уравнений» отведено 8 часов. На данном уроке будет продолжено рассмотрение подходов к решению уравнений, содержащих знак модуля.
Теоретический материал
Теоретический материал к уроку изложен в Приложении 2. Материал содержит примеры решения уравнений.
Методические рекомендации по организации урока. Рекомендации по формативному оцениванию
В начале урока следует уделить время повторению способов решения линейных уравнений, содержащих знак модуля. Для проверки правильности решения заданий учитель может использовать карточки с буквами, которые предлагались на первом уроке. Однако для учащихся будет полезным предварительное обсуждение решений в парах. Затем учитель может записать ответы на доске и организовать общее решение.
Эта предварительная работа призвана облегчить самостоятельное изучение материала о решении квадратных уравнений с модулем. Следует обратить внимание учащихся на то, что они смогут использовать фразы, использованные в объяснении, как образец для объяснения своего решения на следующем этапе урока. Для решения уравнений, приведенных к виду квадратного уравнения использованы такие подходы, как подбор корней по теореме Виета и применение свойства уравнения с нулевой суммой коэффициентов.
Для первичного закрепления и проверки понимания нового материала учащимся предлагается заполнить пропуски в решении несложного уравнения. Далее учащиеся приступают к самостоятельному решению уравнений различной сложности. Количество карточек с уравнениями должно превышать число учащихся, поэтому можно распечатать их в 2-3 экземплярах либо увеличить их число за счет дополнительных заданий, предлагаемых ниже. Учитель для печати карточек может использовать бумагу разных цветов для каждого уровня сложности. Это поможет обеспечить дифференцированный подход на данном этапе урока. Учащиеся смогут работать в соответствии со своими потребностями в своем темпе. Возможность записать своего имени на доске под решенным им уравнением может стимулировать их к более активной работе.
Прием, использованный для формативного оценивания, поможет учащимся своевременно устранять возникающие трудности. Также здесь учащимся предоставляется возможность для развития языковых навыков, формирования коммуникативных навыков. Следует обращать внимание не только на умение учащихся излагать свои идеи. Но и на умение слушать, задавать уточняющие вопросы.
Дополнительные разноуровневые задания
Дополнительные задания:
Уровень А
Уровень В
Уровень С
Ответы и решения
Задания для самостоятельной работы
Уровень А
1. 
Решение.
2. 
Решение.
3. 
Решение.
.
4. 
Решение.
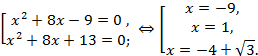
Уровень В
5. 
Решение.
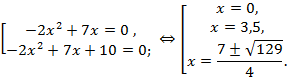
6. 
Решение.
Нет корней.
7. 
Решение.
8. 
Решение.
Уровень С
9. 
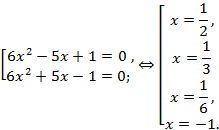
10. 
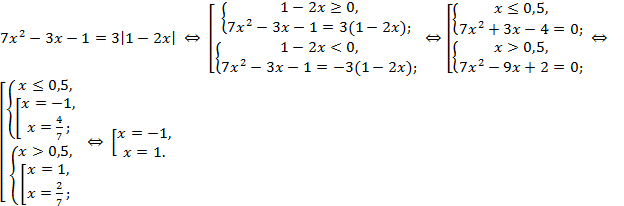
Список полезных ссылок и литературы
1. Кузнецова Е.П., Алгебра: учеб. пособие для 8 кл. учреждений общ. сред. Образования. 2015. – 310с. – ил.
2. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 8 класс : учеб. для учащихся общеобразоват. учреждений – М. : Мнемозина, 2010. – 384 с. : ил.
3. Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Дидактические материалы. 8 класс: пособие для шк. с углубл. изучением математики – М. : Мнемозина, 2010. – 157 с. : ил.
4. Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре, 8-9 классы. – М.: Просвещение, 2009
5.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
