Урок_2_Решение квадратных уравнений_Методические рекомендации

Методические рекомендации к уроку №2 темы/подраздела

«Решение квадратных уравнений»

раздела «8.2А Квадратные уравнения»

Тема урока: Решение квадратных уравнений

Цель обучения:

8.2.2.3 решать квадратные уравнения

На уроке будет рассмотрен вывод формулы корней квадратного уравнения, рассмотрено решение квадратных уравнений с помощью формулы.

Теоретический материал

Можно разделить обе части уравнения на старший коэффициент а, но можно умножить обе части уравнения на 4а, тогда получим следующие уравнение:

,

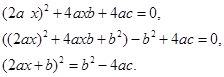
Выражение  называется дискриминантом квадратного уравнения и обозначается буквой D.

Уравнение примет вид:

.

Число корней уравнения зависит от знака дискриминанта.

При D < 0  нет действительных корней.

При D  = 0 уравнение имеет два равных корня:

.

При D > 0 уравнение имеет два различных корня:

.

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

В зависимости от уровня подготовленности класса учитель может предложить учащимся самостоятельно решить квадратное уравнение в общем виде и получить формулу его корней. Либо учитель может использовать диалоговое обучение, чтобы учащиеся в процессе общего обсуждения нашли способ решения.

Для закрепления формулы дискриминанта и формирования понимания зависимости числа корней уравнения от знака дискриминанта учащимся предлагается соответствующее задание, которое будет затем обсуждаться в классе. Учитель должен помогать учащимся в корректном использовании математического языка.

Решение уравнений, используя формулу корней, организовано в форме групповой работы, чтобы создать условия для взаимообучения. Однако учитель может организовать эту работу иначе в соответствии с потребностями своего класса. Это может быть индивидуальная работа с последующей взаимопроверкой или фронтальная работа с классом.

Для более способных учащихся предложено несколько более сложных уравнений.

Дополнительные разноуровневые задания

Уровень В-С

Решите уравнения:

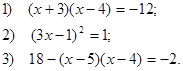
Ответы и решения

Решите уравнения, используя формулу корней:

а) ;

б) ;

в) ;

г) ;

д) ;

е) ;

ж) .

Ответы: а) ; б) , ; в) ; г) ; д) ; е) корней нет; ж)

Список полезных ссылок и литературы

1.      Шыныбеков А.Н. Алгебра: Учебник для 8 класса общеобразовательной школы. – Алматы: Атамұра, 2011. – 288 с.

2.      Мордкович А.Г. Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений. – М. : Мнемозина, 2001. – 223 с. : ил.

3.      Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Дидактические материалы. 8 класс: пособие для шк. с углубл. изучением математики – М. : Мнемозина, 2010. – 157 с. : ил.

4.