Урок_3_Решение дробно-рациональных уравнений_Методические рекомендации (1)

Методические рекомендации к уроку №3 темы/подраздела

«Решение уравнений»

раздела «Квадратные уравнения»

Тема урока: Решение дробно-рациональных уравнений

Цель обучения:

8.2.2.6 решать дробно–рациональные уравнения

На изучение подраздела «Решение уравнений» отведено 8 часов. На данном уроке будет введено понятие дробного рационального (или дробно – рационального) уравнения, рассмотрен алгоритм его решения.

Теоретический материал

Уравнения, левая и правая части которого, являются рациональными выражениями называют рациональными уравнениями.

Рациональные уравнения бывают целыми и дробными. Уравнения  или  является целым, так как и левая и правая части этих уравнений являются целыми выражениями. Уравнения ,  содержат дробные выражения, поэтому являются дробными рациональными.

Алгоритм решения дробно - рациональных уравнений;

1) найти общий знаменатель дробей, входящих в уравнение;

2) умножить обк части уравнения на общий знаменатель;

3) решить получившееся целое уравнение;

4) исключить из корней те, которые обращают в нуль общий знаменатель. Эти корни называют посторонними.

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

Урок начать с проверки правильности выполнения домашнего задания. На данном этапе будет организовано самооценивание учащимися качества своей работы с помощью образцов правильных решений. При необходимости учащиеся могут обсудить в парах возникающие вопросы.

Задания для формативного оценивания достижения цели обучения 8.2.2.5 (решать уравнения вида |ax²+bx|+c=0; ax²+b|x|+c=0) учащимся будут предложена самостоятельная работа.

Устные упражнения на нахождение общего знаменателя рациональных дробей и сложение/вычитание дробей призваны подготовить учащихся к выполнению аналогичных действий с дробями при решении уравнений.

Изучение нового материала следует начать с введения понятия дробного рационального уравнения. Учащиеся сравнивая и анализируя уравнения, которые относятся к разным группам, могут самостоятельно прийти к получению определения дробного рационального уравнения, так как в седьмом классе уже обсуждался вопрос о целом и дробном рациональном выражении. Однако, прежде чем приступить к изучению способа решения дробно-рациональных уравнений целесообразно решить целые уравнение, в записи которого использованы дробм, например,  . Это поможет учащимся проложить «мостик» от имеющихся знаний и навыков к приобретению новых. После того, как учащиеся самостоятельно решат данное уравнения нужно обсудить этапы решения, записывая их на доске или слайде презентации в виде алгоритма. Затем можно приступать к решению дробных уравнений. Сделав проверку, учащиеся могут убедиться, что не все корни полученного целого уравнения являются корнями исходного дробно-рациональныго уравнения. Полезно дать учащимся время для обдумывания вопроса о том, почему так произошло. После введения понятия постороннего корня, можно обсудить с учащимся другой порядок оформления решения, где первоначально определяется область допустимых значений уравнения, а на последнем этапе проверяется принадлежность корней этой области. Учащиеся должны привлекаться к комментированию каждого этапа решения. Следует обратить внимание учащихся. что они должны обращать внимание на фразы, которые при этом используют учитель и другие учащиеся, так как в конце урока каждый из них будет объяснять другим решение одного из уравнений.

Для организации работы по выработке навыка решения дробно-рациональных уравнений выбрана стратегия Jigsaw, так как учащиеся на первоначальном этапе могут испытывать затруднения, особенно, если навык преобразования рациональных выражений недостаточно высок.

В конце урока предложены два уравнения разного уровня сложности для самостоятельного решения. В зависимости от уровня подготовленности учащихся учитель может предложить учащимся работу в парах, чтобы учащиеся могли помогать друг другу. Также учащиеся могут выбрать для решения одно из уравнений в соответствии со своими потребностями.

Дополнительные разноуровневые задания

Решите следующие уравнения:

Уровень В

Уровень С

Ответы и решения

Задания для работы в группах

1)  

Решение.

Ни один из корней не обращает общий знаменатель в 0, поэтому числа 0,5 и 1 являются корнями данного уравнения.

2)  

Решение.

Ни один из корней не обращает общий знаменатель в 0, поэтому числа 4 и 5 являются корнями данного уравнения.

3)  

Решение.

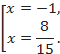
Ни один из корней не обращает общий знаменатель в 0, поэтому полученные числа являются корнями данного уравнения.

Задания для самостоятельного решения

а) ;

б) .

Решение.

а)

Корни уравнения – числа -1 и -4,7, так как они принадлежат области допустимых значений переменной.

б)

После упрощения получим:

.

Ни один из корней не обращает общий знаменатель в 0, поэтому числа -9 и 2 являются корнями данного уравнения.

Список полезных ссылок и литературы

1.                   Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 8 класс : учеб. для учащихся общеобразоват. учреждений  – М. : Мнемозина, 2010. – 384 с. : ил.

2.                   Зив Б.Г., Гольдич В.А. Дидактические материалы по алгебре для 8 класса. – С.-Петербург: Петроглиф, 2010. -128 с. : ил.

3.                   Скачано с www.znanio.ru