Урок_4_Решение квадратных неравенств_Методические рекомендации (1)

Методические рекомендации к уроку №4

темы/подраздела «Квадратное неравенство»

раздела «Неравенства»

Тема урока: Решение квадратных неравенств

Цель обучения:

8.2.2.8 решать квадратные неравенства

Учащиеся продолжат работу по формированию навыка решения квадратных неравенств. На данном уроке будет рассмотрен еще один способ решения неравенств, когда произведение или частное двух чисел сравнивается с нулем.

Теоретический материал

Теорема 1

Пусть . Тогда каждое из следующих неравенств

, ,

равносильно двойному неравенству .

Доказательство.

Произведение (частное) двух чисел отрицательно, если эти числа имеют разные знаки, тогда, учитывая, что , имеем:

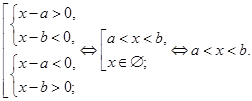
Теорема 2

Пусть . Тогда каждое из следующих неравенств

, ,

равносильно совокупности неравенств

Доказательство.

Произведение (частное) двух чисел положительно, если эти числа имеют одинаковые знаки. Следовательно,  

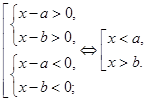
Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

Доказательства утверждения не являются сложными, поэтому отдельные учащиеся могут самостоятельно получить его. Доказательство второго утверждения можно поручить учащимся найти и оформить в тетради, затем обсудить у доски.

После рассмотрения каждого из утверждений учащимся предлагаются задания для устного решения. Использование мини-досок для записи ответов позволит учителю быстро оценить уровень понимания материала.

Для письменного решения предлагаются задания разного уровня сложности. Учащиеся могут использовать выводы, полученные ранее, и записать сразу ответ. Либо они могут в каждом задании рассматривать совокупность систем неравенств, как это было сделано при доказательстве теорем в начале урока.

Ответы и решения

Уровень А

1. Решите неравенства:

а) ;

б) ;

в) ;

г) .

Ответ: а) ; б) ; в) ;

г) .

Уровень В

Найдите все целые числа, удовлетворяющие неравенству:

а) ;

б) ;

в) ;

г) .

Ответ: а) 1, 2, 3, 4, 5; б) Ø; в) -3, -2, -1, 0; г) -2, -1, 0, 1, 2.

Уровень С

Верно ли, что множество решений неравенства  содержится в интервале ? 

Решение.

Найдем корни квадратного трехчлена :

,  и .

.

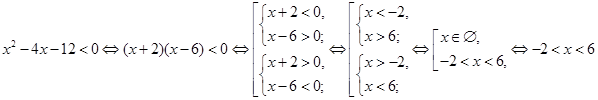Полученные решения содержатся в интервале .

Список полезных ссылок и литературы

1.      Виленкин Н.Я., Виленкин А.Н., Сурвилло Г.С. и др. Алгебра: учеб. для 8 кл.  с углубленным изучением математики.  – М.: Просвещение, 2006. 303 с. : ил.

2.      Мордкович А.Г. и др. Алгебра. 8 кл.: В двух частях. Ч. 2: Задачник для общеобразоват. учреждений. М.: Мнемозина, 2003. – 239 с: ил.

3.      Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре, 8-9 классы.  – М.: Просвещение, 2009. 301 с.: ил.

4.