Урок_5_Биквадратные уравнения_Методические рекомендации

Методические рекомендации к уроку №5 темы/подраздела

«Решение уравнений»

раздела «Квадратные уравнения»

Тема урока: Решение уравнений, приводимых к квадратным. Биквадратные уравнения

Цель обучения:

8.2.2.7 решать уравнения, приводящиеся к виду квадратного уравнения

Это пятый урок указанного подраздела, состоящего из 8 уроков. На данном уроке будет рассмотрено применение метода замены переменной для решения биквадратных уравнений и других уравнений 4-й степени.

Теоретический материал

Уравнения вида , где а ≠ 0, называют биквадратными.

Для решения биквадратных уравнений надо:

1) сделать подстановку ;

2) найти корни  и  квадратного уравнения ;

3) решить уравнения  и  (они имеют корни лишь в том случае, когда  и ).

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

В начале урока предусмотрено повторение методов решения квадратных уравнений. Следует попросить учащихся поочередно использовать эти методы позднее при переходе к квадратным уравнениям после выполнения замены.

При изучении темы урока используется диалоговое обучение. При решении заданий на закрепление новых способов действий учитель обходит класс, консультирует учащихся, дает советы, задает наводящие вопросы. Ученики должны знать, что они будут объяснять решения другим группам, это будет стимулировать их к более активному участию в работе группы. Во время обсуждения решений в новых группах учащиеся по очереди представляют свои решения остальным, после чего происходит обсуждение решение и оценивание по имеющимся дескрипторам. Учащиеся должны также обращать внимание на корректность использования математического языка и оформление решения.

Возможно учащиеся решат не все уравнения, важно, чтобы они понимали идею решения уравнений методом введения новой переменной и правильно применяли алгоритм. В плане урока их содержится достаточно большое количество разного уровня сложности с учетом потребностей сильных учащихся. Но учитель может уменьшить число уравнений, предлагаемых для решения в классе и дома.

Ответы и решения

Работа в группах

1)

Ответ: .

2)

Ответ: .

3)

Ответ: .

4)                        

Ответ: 3; -3

5)

Решение.

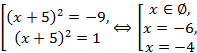
Ответ: -6; -4.

6)            

Решение.

Ответ: -4; -2; 2; 4.

7)                          

Решение.

Ответ: 49.

8)                   

Решение.

Ответ: -7; 4.

Дополнительные разноуровневые задания

1.  

2.  

Список полезных ссылок и литературы

1.      А.Н.Шыныбеков Алгебра 8- сынып - А.: «Атамұра» 2012 ж

2.      Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре, 8-9 классы.  – М.: Просвещение, 2009. 301 с.: ил.

3.