Урок_5_Квадратное неравенство_Методические рекомендации (1)

Методические рекомендации к уроку №5

темы/подраздела «Квадратное неравенство»

раздела «Неравенства»

Тема урока: Решение квадратных неравенств

Цель обучения:

8.2.2.8 решать квадратные неравенства

Это завершающий урок темы Квадратные неравенства. Работа учащихся направлена на комплексное применение знаний и навыков по данной теме, причем задания интегрированы с некоторыми ранее изученными темами.

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

В процессе проверки домашней работы учитель организует беседу о различных подходах к решению квадратных неравенств – с применением эскиза параболы или с помощью перехода к совокупности систем линейных неравенств.

Работа в группах организована таким образом, что сначала учащимся дается возможность самостоятельно решить предложенные задания. Причем учащиеся работают в ограниченном промежутке времени (2 минуты) от одного сигнала учителя до другого (для подачи сигнала можно использовать обычный колокольчик). В зависимости от уровня класса учитель может как уменьшить, так и увеличить время, отведенное на выполнение задания. Для формативного оценивания работ используется прием взаимооценивания с использованием образцов ответов. Важным моментом является выполнение работы над ошибками, нужно, чтобы учащиеся нашли и исправили свои ошибки. При возникновении затруднений они могут обратиться за консультацией к ученику, проверявшему это задание, либо к другому члену группы, выполнившему задание. Для учащихся, которые закончат эту работу раньше отведенного времени, предусмотрены дополнительные задания.

Рефлексия результатов данной работы поможет учителю и учащимся понять какие трудности возникают у учащихся, и на следующих уроках предусмотреть задания, направленные на их преодоление.

Задания для формативного оценивание цели обучения урока соответствуют критерию «умеет решать квадратные неравенства», поэтому здесь предлагаются задания на применение навыка.

Дополнительные разноуровневые задания

Уровень В

Верно ли, что неравенство  верно при любом х?

Уровень С

Среди всех чисел, удовлетворяющих неравенству , найдите те, которые удовлетворяют неравенству .

Ответы и решения

Карточки для работы в группе:

1) Сколько целочисленных решений имеет неравенство ?

Решение.

Первый способ:

Найдем корни квадратного трехчлена :

 или .

Так как нужно найти целые решения неравенства, то найдем приближенные 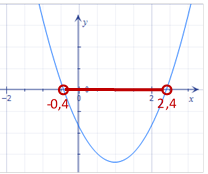значения корней с точностью до десятых:

Отметим на числовой оси полученные корни и схематично изобразим параболу, проходящую через эти точки, ветви которой направлены вверх.

Целые решения неравенства – числа 0, 1и 2.

Ответ: 3.

Второй способ:

Найдем корни квадратного трехчлена :

 или .

Отсюда,

Согласно теореме, если , то неравенство , равносильно двойному неравенству . Значит решением данного неравенства является промежуток .

Либо можно рассмотреть совокупность условий:

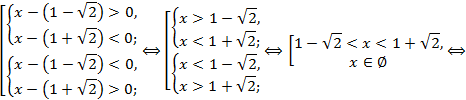
Так как нужно найти целые решения неравенства, то найдем приближенные значения корней с точностью до десятых:

Целые решения неравенства – числа 0, 1и 2.

Ответ: 3.

2)  Решите неравенство  и укажите сумму всех его целочисленных решений.

Решение.

Первый способ:

Перенесем произведение  из правой части неравенства в левую:

Вынесем общий множитель  за скобки:

Вынесем из скобок числовые множители 3 и -4:

Согласно теореме, если , то неравенство , равносильно двойному неравенству . Значит решением данного неравенства является промежуток . В этом промежутке два целых числа – 0 и 1, их сумма равна 1.

Первый способ:

Раскроем скобки в правой части неравенства, затем перенесем все слагаемые из правой части неравенства в левую:

Так как сумма коэффициентов квадратного трехчлена равно нулю, то один из его корней равен 1, а второй равен .

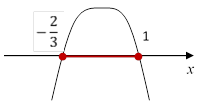Отметим на числовой оси полученные корни и схематично изобразим параболу, проходящую через эти точки, ветви которой направлены вниз.

Решением данного неравенства является промежуток . В этом промежутке два целых числа – 0 и 1, их сумма равна 1.

Ответ: 1.

3) Какие из чисел -1000237, , π, 6,(3),  удовлетворяют неравенству ?

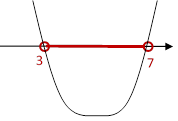Решение.

Корни квадратного трехчлена  равны 3 и 7. Построим эскиз параболы, ветви которой направлены вверх. Решением данного неравенства является промежуток (3; 7). Из данных чисел в указанном промежутке лежат числа π и 6,(3).

Ответ: π и 6,(3).

4) Решите неравенство .

Решение.

Раскроем скобки в обеих частях неравенства:

Ответ:

5) Найдите промежутки знакопостоянства функции .

Решение.

Найдем нули функции:

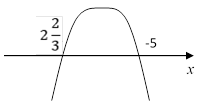Так как ветви параболы направлены вниз, то функция принимает положительные значения на промежутке , а отрицательные – на каждом из промежутков  и .

Ответ: y > 0 при , y < 0 при .

Список полезных ссылок и литературы

1.      Виленкин Н.Я., Виленкин А.Н., Сурвилло Г.С. и др. Алгебра: учеб. для 8 кл.  с углубленным изучением математики.  – М.: Просвещение, 2006. 303 с. : ил.

2.       Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феоктистов И.Е. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений.  – М.: Мнемозина, 2010

3.      Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре, 8-9 классы.  – М.: Просвещение, 2009. 301 с.: ил.