Урок_6_Уравнения, приводимые к квадратным_Методические рекомендации (1)

Методические рекомендации к уроку №6 темы/подраздела

«Решение уравнений»

раздела «Квадратные уравнения»

Тема урока: Решение уравнений, приводимых к квадратным

Цель обучения:

8.2.2.7 решать уравнения, приводящиеся к виду квадратного уравнения

Шестой урок указанного подраздела, состоящего из 8 уроков, ставит целью развитие навыка применения метода замены переменной для решения уравнений.

Теоретический материал

Уравнения вида , где а ≠ 0, можно привести к квадратному уравнению, используя подстановку . В результате подстановки получают уравнение  и находят его корни  и . Возвращаясь к замене, решают уравнения  и .

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

В начале урока предлагаются несложные задания на повторение, здесь от учащихся ожидается высокая скорость работы – не более 30 секунд на выполнение каждого задания. Рекомендуется использовать маркерные доски, чтобы учитель мог оценить кто из учащихся не справляется с работой и наметить пути устранения трудностей.

Способ решения уравнений путем подстановки был рассмотрен на предыдущем уроке для более простого случая – биквадратных уравнений. На данном уроке продолжается работа по формированию навыка применения этого способа. Трудность может заключаться в нахождении подходящей замены и получении корректного квадратного уравнения. Поэтому после обсуждения метода учащимся предлагается несколько устных упражнений на отработку указанных шагов в решении уравнений путем введения новой переменной.

Работа по применению способа на практике проходит в парах, чтобы учащиеся могли совещаться, сравнивать результаты на промежуточных этапах. В процессе взаимооценивания работ было бы полезным предоставить возможность отвечающему ученику обосновать свои решения, проговорить этапы решения, а проверяющему – высказать комментарии по поводу работы, не ограничивая эту работу простановкой плюсов и минусов в листе оценивания.

Домашнее задание дается дифференцированно, каждый учащийся самостоятельно выбирает уровень сложности уравнений.

Дополнительные разноуровневые задания

Уровень В

Найдите сумму квадратов корней уравнения .

Выполните задание двумя способами:

а) решив данное уравнение;

б) не решая уравнение.

Уровень С

Решите уравнение

Ответы и решения

Работа в парах

Решите уравнения: 

1) ;

2) ;

3) ;

4) .

Решения.

1) Пусть , тогда

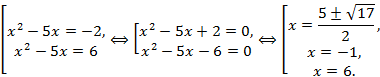
2) Пусть , тогда

3)

Пусть , тогда

4) Пусть , тогда

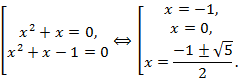
Список полезных ссылок и литературы

1.      Галицкий М.Л., Гольдман А.М., Звавич Л.И. Сборник задач по алгебре, 8-9 классы.  – М.: Просвещение, 2009. 301 с.: ил.

2.      Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Дидактические материалы. 8 класс: пособие для шк. с углубл. изучением математики – М. : Мнемозина, 2010. – 157 с. : ил.

3.