Урок_7_Решение квадратных уравнений. Теорема Виета_Методические рекомендации

Методические рекомендации к уроку №7 темы/подраздела

«Решение квадратных уравнений»

раздела «8.2А Квадратные уравнения»

Тема урока: Решение квадратных уравнений. Теорема Виета

Цели обучения:

8.2.2.3 решать квадратные уравнения;

8.2.2.4 применять теорему Виета

Урок является завершающим в серии уроков данной темы. Учащиеся будут выполнять задания для фомативного оценивания приобретенных знаний и умений.

Методические рекомендации по организации урока. Рекомендации по формативному оцениванию

В начале урока будет рассмотрено решение квадратных уравнений путем подбора корней на основании теоремы Виета. Также будет уделено внимание решению других заданий с применением теоремы Виета. Учитель организует обсуждение с оформлением решения на доске. Следует предоставлять учащимся больше времени на размышление и формулирование ответа. Это поможет вовлечь всех учащихся в процесс обсуждения.

Для формативного оценивания целей обучения учащимся предлагаются разнообразные задания. Учителю нужно наблюдать за процессом взаимооценивания, учащиеся должны не просто показывать друг другу полученный ответ, они должны объяснять последовательность выполненных действий, обосновывая каждый шаг решения. Это будет способствовать более прочному запоминанию и более глубокому пониманию материала.

Ответы и решения

Пример 3.

Найти все р, при каж­дом из ко­то­рых от­но­ше­ние кор­ней уравнения  равно 12.

Ре­ше­ние.

При неко­то­рых зна­че­ни­ях р урав­не­ние может во­об­ще не быть кор­ней, при дру­гих зна­че­ни­ях корни будут различными, но нужно найти такие зна­че­ния па­ра­мет­ра, при ко­то­рых корни от­ли­ча­ют­ся в 12 раз.

Сфор­ми­ру­ем си­сте­му условий:

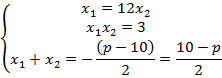
Мы по­лу­чи­ли си­сте­му трех урав­не­ний от­но­си­тель­но трех неиз­вест­ных: ,  и р. За­ме­тим, что пер­вые два урав­не­ния за­ви­сят толь­ко от  и , если мы их найдем, то под­ста­вим в тре­тье урав­не­ние, то най­дем значение р.

Рас­смот­рим оба ва­ри­ан­та:

Под­став­ля­ем в тре­тье урав­не­ние:

Пер­вый ответ по­лу­чен.

Под­став­ля­ем в тре­тье урав­не­ние:

Ответ: -3; 23.

Сде­ла­ем сле­ду­ю­щее при­ме­ча­ние: при най­ден­ных р си­сте­ма

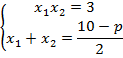
имеет ре­ше­ние, зна­чит, и само квад­рат­ное урав­нение

имеет ре­ше­ние.

Индивидуальная работа

1. Сумма корней квадратного уравнения  равна 16. Найдите значение р.

Ответ: 0.

2. Один из корней уравнения  равен 12,5. Найдите значение с и второй корень уравнения.

Ответ: .

3. Решите уравнение  и сделайте проверку с помощью теоеремы Виета.

Ответ: 1; -4/7

4. Один из корней уравнения х² + рх – 35 = 0  равен 7. Найдите второй корень уравнения и значение р.

Ответ: -2.

5. Вычислите значение выражения а ± в + с, затем решите уравнения:

а)  х² + 5х – 6 = 0;

б) 6 х²  +5х – 1 = 0;

в) 3 х²  - 8х  + 5 = 0;

г) 345 х²  +137х – 208 = 0.

Ответ: а) -6 и 1; б) -1 и 1/6; в) 1 и 5/3; -1 и 208/345.

6. Выразите сумму квадратов корней уравнения х² + рх + q = 0  через р и q.

Ответ: .

7. Составьте квадратное уравнение, корнями которого являются числа:

а) -3 и 8; б) и .

Ответ: а) ; б) .

8.  - корни уравнения . Не вычисляя корни, найдите значение выражения .

Ответ: 66.

9. Один из корней уравнения  втрое больше другого. Найдите корни и значение с.

Ответ: корни 0,6; 1,8; с = 1,08.

10.  - корни уравнения . Известно, что . Найдите р.

Ответ: 15.

11.  - корни уравнения х² + рх + q = 0. Составьте квадратное уравнение, имеющее корни:

а) ; б) .

Ответ: а) х² + (р-4)х + q = 0; б) х² + рх + q + 2р + 4 = 0.

Список полезных ссылок и литературы

1.      Шыныбеков А.Н. Алгебра: Учебник для 8 класса общеобразовательной школы. – Алматы: Атамұра, 2011. – 288 с.

2.      Мордкович А.Г. Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений. – М. : Мнемозина, 2001. – 223 с. : ил.

3.      Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Дидактические материалы. 8 класс: пособие для шк. с углубл. изучением математики – М. : Мнемозина, 2010. – 157 с. : ил.

4.