УРОК 23 Тема: Подготовка к контрольной работе.

УРОК 40

Тема: Числовые промежутки

Цели деятельности учителя: создать условия для формирования представлений о числовых промежутках, о  нестрогом и строгом неравенствах, о числовом отрезке  и интервале; находить соответствие между условием, названием числового промежутка, графической моделью, аналитической моделью и символической записью.

 Планируемые результаты изучения темы:

Личностные: участие в диалоге, подбор аргументов для доказательства своей позиции, анализ текста.

Предметные: имеют представление о числовых промежутках, о нестрогом и строгом неравенствах, о числовом отрезке и интервале.

 Метапредметные результаты изучения темы (универсальные учебные действия):

познавательные: проводить сравнение, сериацию и классификацию по заданным критериям;

регулятивные: различать способ и результат действий;

коммуникативные: договариваться и приходить к общему решению совместной деятельности, в том числе в ситуации столкновения интересов.

Сценарий урока.

I.Устная работа.

- На доске изображена координатная прямая: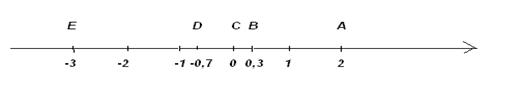

- Какие условия задают координатную прямую?

(должно быть отмечено начало координат, выбран единичный отрезок)

- Как называется число, которое соответствует точке на такой прямой?

(координатой точки)

- Какие координаты имеют точки А, В, С и т. д.?

(А (2), В(0,3), С(0), D(-0,7), Е(-3)).

-  Сравните числа с помощью координатной прямой

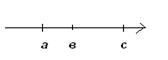
а) а и в; (а < b)

б) а и с. (а < с)

- Какое из этих чисел расположено правее всего на координатной прямой (левее всего) 3; 2,5; -6; -3,8?

(правее всего  - 3, а левее – (-6))

- На рисунках изображены числа на координатной прямой. Все ли сделанные рисунки правильные?

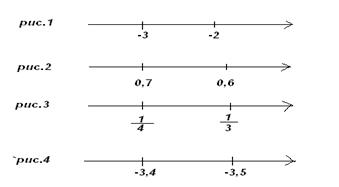
(на втором и четвертом  рисунках числа надо поменять местами)

II.Работа с текстом учебника. Изучение нового материала.

- Прочитайте текст параграфа на стр. 73-74.

- Какие записи и рисунки сделаете в тетрадях?

(Перечертим рисунок 59 и напишем, что множество точек, записанное в виде (а; +∞) называется открытым лучом, а в виде неравенства х > а,  полученное неравенство называется строгим).

- Как вы думаете, почему неравенство назвали строгим?

(Ребята высказывают свои предположения)

- Еще что-то причитали новое? Что записали в тетрадях?

(Перечертили рисунки 61 и 62. Множество точек, записанное в виде [а; +∞)  является геометрической моделью неравенства

х ≥ а, а данное неравенство называется нестрогим).

- Рассмотрите рисунки 64 и 65. Чем они отличаются от тех, которые вы уже рассмотрели.

(Ребята говорят, что на числовой прямой расположены два числа. Штриховка идет от одного числа к другому).

- Прочитайте, как называются такие промежутки. Как называются неравенства, решения которых изображены на этих рисунках.

(На рисунке 64 изображен интервал, на рисунке 65 изображен отрезок. Неравенства, решения которых изображаются в виде интервала или отрезка, называются двойными).

III.Выполнение упражнений на закрепление изученного материала.

1.      Выполните № 333

Решение: а) 2≤ х ≤ 7, [2; 7]   б) -8 ≤ х ≤ -2, [-8; -2]

в) -5 < х < 0, (-5; 0)   г) -7 ≤ х ≤ 7, [-7; 7].

2. Самостоятельно выполните № 334.

Проверка решения:

а) 1,5 ≤ х ≤ 1,9, [1,5; 1,9]   б) -0,7 ≤ х ≤ -0,2, [-0,7; -0,2]

в) -3,4 < х < 0, (-3,4; 0)   г) -5,9 ≤ х ≤ 5,9, [-5,9; 5,9].

3. Под комментарии с места выполните № 336.

Комментарии: а) открытый луч, х > 3;

б) отрезок, -9 ≤ х ≤ -5;   в) луч, х < -8;   г) интервал, -4< х< 4.

IV.Выполнение заданий на повторение.

1.      Выполните № 360 (а,б) и № 361 (а,б)

Решение: № 360

а) -5,48 –(-1,52)+7,42-8,01-7,42-(-5,48) = -5,48 + 1,52 + 7,42 –

 -8,01 – 7,42 + 5,48 = (-5,48 + 5,48) + (7,42 – 7,42) + 1,52 –

- 8,01 = - 6,49;

б) 9,49 – (-1,37) – 1,1 – 9,49 – (+ 2,31) – 0,27 = 9,49 + 1,37 –

 -1,1 – 9,49 – 2,31 – 0,27 =  (9,49 – 9,49) + (1,37 – 0,27 – 1,1) – 2,31 = - 2,31.

№ 361

а) -0,25 + (7,23 – 4, 08) = -0,25 + 3,15 = 2,9

б) -7,84 – (-2,6 – 3,4) = -7,84 + 6 = - 1,24.

V. Итог урока. Рефлексия.

- С каким понятием познакомились на уроке?

- Можете перечислить виды числовых промежутков?

Домашнее задание: 337,337, 360 (в,г).