Урок: ЧИСЛОВАЯ ОКРУЖНОСТЬ НА КООРДИНАТНОЙ ПЛОСКОСТИ

Урок:
Числовая окружность
на координатной пЛОСКОСТИ

УМК Алгебра и начала математического анализа, 10-11 классы. В 2. Ч.1. Учебник для общеобразовательных учреждений (базовый уровень) /А.Г. Мордкович. – 10-еизд., стер.- М.: Мнемозина,2013.  Ч.2. Задачник для общеобразовательных учреждений (базовый уровень) /[А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. – 10-еизд., стер.- М.: Мнемозина,2013. 

Уровень обучения. Базовый

Цели: ввести понятие модели числовой окружности в декартовой и криволинейной системе координат; формировать умение находить декартовы координаты точек числовой окружности и выполнять обратное действие: зная декартовы координаты точки, определять её числовое значение на числовой окружности.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Назовите координаты точек плоскости:

2. Назовите число, соответствующее заданной точке на числовой окружности.

III. Объяснение нового материала.

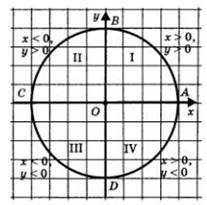
1. Объяснение проводи согласно пункту учебника. Разместив числовую окружность в декартовой системе координат, подробно разбираем свойства точек числовой окружности, находящихся в различных координатных четвертях.

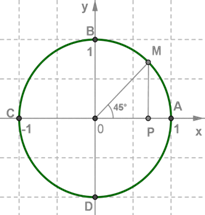        Точка M(π4) середина I четверти.

Опустим перпендикуляр MP на прямую OA и рассмотрим треугольник OMP.

Так как дуга AM составляет половину дуги AB, то ∡MOP=45° 

 Значит, треугольник OMP - равнобедренный прямоугольный треугольник и OP=MP, т.е. у точки M

абсцисса и ордината равны: x=y.

    Так как координаты точки M(x;y) удовлетворяют уравнению числовой окружности x²+y²=1, то для их нахождения нужно решить систему уравнений:

x²+x²=1

2x²=1

x²=1/2

у=x=2√2

Получили, что координаты точки M, соответствующей числу π/4 будут   M(π/4)=M(2√2;2√2)

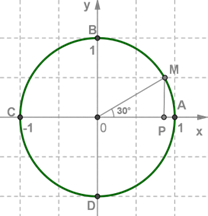       Треугольник MOP прямоугольный. Так как дуга AM составляет третью часть дуги AB, то ∡MOP=30°.

 Катет MP лежит против угла 30 градусов в прямоугольном треугольнике, значит, равен

    половине гипотенузы, т.е. ордината точки M равна

 MP=1/2   y=1/2

Абсциссу x точки M найдём, решив уравнение:

 x²+y²=1

x²=1−(1/2)²=1−1/4=3/4   x=3√2

При решении учитываем, что абсцисса точки M положительна.

Получили, что координаты точки M, соответствующей числу π/6 будут M(π/6)=M(3√2;1/2)

2. Методическая «игра» – отыскание декартовых координат «хороших» точек числовой окружности. Речь идет о переходе от записи М(t) к М (х; у). (презентация слайд 1)

3. Методическая «игра» – отыскание знаков координат «плохих» точек числовой окружности. Если, например, М(2) = М (х; у), то х < 0; у > 0. (презентация слайд 2)

IV. Формирование умений и навыков.

1. № 5.1 (а; б), № 5.2 (а; б), № 5.3 (а; б).

Данная группа заданий направлена на формирование умения отыскивать декартовы координаты «хороших» точек на числовой окружности.

Решение:

№ 5.1 (а).

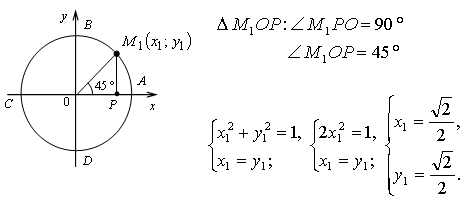
2. № 5.4 (а; б), № 5.5 (а; б).

Эта группа заданий направлена на формирование умений находить криволинейные координаты точки по её декартовым координатам.

Решение:

№ 5.5 (б).

3. № 5.10 (а; б).

Данное упражнение направлено на формирование умения находить декартовы координаты «плохих» точек.

V. Итоги урока.

Вопросы учащимся:

– Что собой представляет модель – числовая окружность на координатной плоскости?

– Как, зная криволинейные координаты точки на числовой окружности, найти её декартовы координаты и наоборот?

Домашнее задание: № 5.1 (в; г) – 5.5 (в; г), № 5.10 (в; г).