
Публикация является частью публикации:
Док-во:
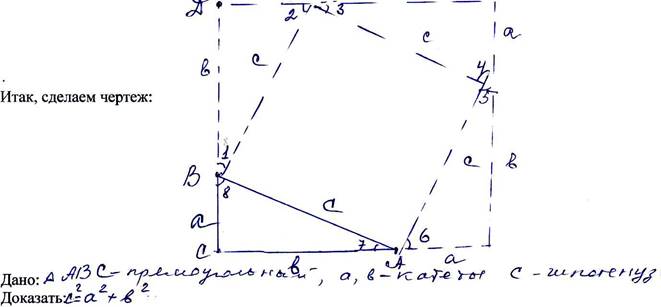
Для док-ва давайте достроим прямоугольный треугольник до квадрата со стороной а + в; Для этого продолжим на сторону ВС, на ней отложим отрезок в.
![]() Обозначим точку
D, и продолжим сторону ВС, на его продолжении отложим отрезок,
Обозначим точку
D, и продолжим сторону ВС, на его продолжении отложим отрезок, ![]() равный «в» и
обозначим . Е. Из ТОЧУИ D проведем DF Н СЕ;
равный «в» и
обозначим . Е. Из ТОЧУИ D проведем DF Н СЕ;![]()
Из точки Е проведем EF // CD; А точку пересечения Р,
От точки F отложим а на DF — обозначим М и от точки К на FE отложим в — обозначим К.;
Проведем отрезки АМ, МК, ВК.
Вопрос: Из каких фигур состоит данная фигура?
- из квадрата и 4-х прямоугольных треугольников.
Как связаны между собой эти треугольники?
-
равны.![]()
Почему? По
какому равенству? СУС мили по признаку равенства прямоугольных ![]() треугольников?
треугольников?
Обозначаю гипотенузы через С
РА какие углы равны? Обозначу, а![]() скажет,
какие углы равны
скажет,
какие углы равны ![]()
![]() z/=a5
z/=a5![]()
![]() Обратим внимание на
4-хугольник? Что вам о нем известно?
Обратим внимание на
4-хугольник? Что вам о нем известно?
-
стороны равны![]()
-
Чем может являться 4-хуголькик, у которого стороны равны?![]()
- ромбом или квадратом.
-
Что нужно знать, что он является квадратом?![]()
- доказать, что углы прямоугольные. , Как?
т.к являются острыми углами прямоугольного треугольника.
Поэтому![]()
Также все остальные углы равны
Значит, 4-хугольник является квадратом. S Д = (4 + К) ![]()
•А как можно найти площадь этого квадрата. Т.е. из каких фигур состоит? -как сумму площадей 1 кв-та и 4-х треугольников, т.е.
![]()
![]() Итак,
Итак,  с
одной стороны с 9--79 2-0,
с
одной стороны с 9--79 2-0,![]()
- Итак, каким методом мы пользовались?
![]() в чем суть данного
метода? Для какого треугольника применима Треорма Пифагора?
в чем суть данного
метода? Для какого треугольника применима Треорма Пифагора?
-
только для прямоугольных треугольников, 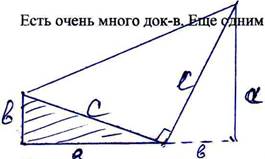 им док-м
является: (сои .
им док-м
является: (сои . ![]() )
)
Получилась трапеция. Чему равна площадь трапеции? (вызвать Аню, чтобы док-ть на доске).
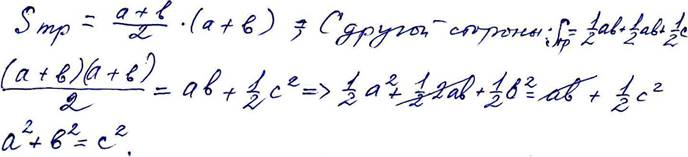
![]() //l А теперь небольшое
сообщение из истории математики сделает Лена •
//l А теперь небольшое
сообщение из истории математики сделает Лена •
1.
пье-в-ре-.—еьу—--![]()
З.
4. Про древний трактат теоремы:
Площадь квадрата, построенного на гипотенузе прямоугольного треуг-ка, равный сумме площади квадратов, построенных на его катетах- Лена док-т как в Др. Греции доказывали молчаливым способом, т.е. «смотри».
Для частного случая — равнобедренный прямоугольнб№треуг-к:
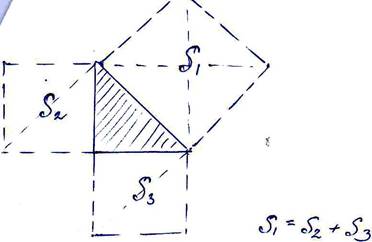
Почему?
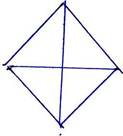
Объяснение: я проведу диагонали и вижу: 4 треуг-ка, а там по 2 треуг-ка. А случай, когда треуг-к неравнобедренный, подумайте дома. Докажите..
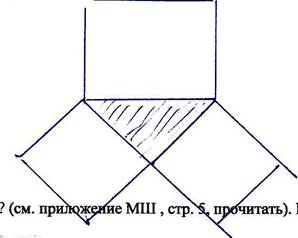
![]() Перевернем :
Перевернем :
На
что похоже? (см. при ж читать). Рисунок
(шаржи).![]()
![]()
![]() Док-во: Теореу
Пифагора учащиеся ср.веков считали очень трудным и называли его
Док-во: Теореу
Пифагора учащиеся ср.веков считали очень трудным и называли его ![]() «ослиный мост»
или «бегство убогих», т.к. некоторые «убогие» Ученики, не имевшие серьезной
математической подготовки, бежали от геометрии. Слабые ученики, заучившие
теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в
состоянии преодолеть Теоремы Пифагора, служившую для них в качестве
непреодолимого моста. Из- за чертежей, сопровождающих Теоремы Пифагора,
учащиеся, называли ее также «ветреной мельницей»,
«ослиный мост»
или «бегство убогих», т.к. некоторые «убогие» Ученики, не имевшие серьезной
математической подготовки, бежали от геометрии. Слабые ученики, заучившие
теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в
состоянии преодолеть Теоремы Пифагора, служившую для них в качестве
непреодолимого моста. Из- за чертежей, сопровождающих Теоремы Пифагора,
учащиеся, называли ее также «ветреной мельницей», ![]() составляли стихи вроде
«Пифагора штаны во все стороны равны», рисовали карикатуры (показать рисунки).
составляли стихи вроде
«Пифагора штаны во все стороны равны», рисовали карикатуры (показать рисунки).
![]() Итак, какие задачи мы можем решать с
помощью Пифагора, сочините.
Итак, какие задачи мы можем решать с
помощью Пифагора, сочините. ![]() - можно находить длину одной стороны, если
известны другие.
- можно находить длину одной стороны, если
известны другие.
![]() V Закрепление.
V Закрепление.![]()
![]() Устно:
Устно:
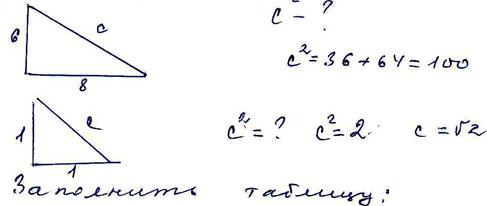 1. 2
1. 2
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
5 |
|
|
|
|
|
3. 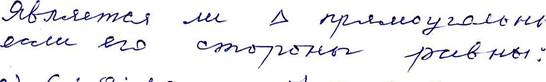 、/
、/
りノ・丿/っ ソぅク
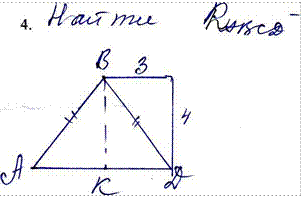
 フ
フ 
7冖戸′を
 FIH(þaropa.
FIH(þaropa.
井プ /し廴ー
ク~丿![]()
Выводы:л ![]()
1.
2.
Теоремы Пифагора — Д/дО'ДеьГа--ГД![]()

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.