
ПЛАН –КОНСПЕКТ УРОКА
Тема урока: Вычисление угла между двумя прямыми
Цели урока:
· повторение и закрепление знаний по теме угол между двумя прямыми;
· развитие пространственного и логического мышления;
· воспитание интереса к изучению предмета.
Задачи:
образовательные (формирование познавательных УУД):
Напомнить определение угла между двумя прямыми; научить использовать формулу для нахождения угла между двумя прямыми; применять полученные знания для решения типичных задач ЕГЭ .
воспитательные (формирование коммуникативных и личностных УУД):
участвовать в коллективном обсуждении проблем и взаимоуважение собеседников, воспитывать внимание, ответственность и аккуратность.
развивающие (формирование регулятивных УУД)
развивать умение анализировать, сравнивать, обобщать, делать выводы, выбирать способы решения задач в зависимости от конкретных условий; контроль и оценка процесса и результатов деятельности.
Планируемые результаты. Умение:
выполнять параллельный перенос прямых;
применять формулу для вычисления угла между прямыми,
рассуждать и делать выводы;
оценивать результаты своей деятельности.
Тип урока: повторение изученного материала.
Методы обучения:
словесные (при формировании теоретических и фактических знаний);
наглядные (для развития наблюдательности, повышения внимания и лучшего запоминания материала);
проблемно – поисковые (для развития самостоятельности мышления, исследовательских умений, творческого подхода к делу);
методы контроля и самоконтроля (рефлексии).
Формы работы учащихся: Фронтальная, индивидуальная.
Необходимое техническое оборудование: компьютер, проектор.
ХОД УРОКА
|
Орг. Момент. Приветствие. |
-Здравствуйте, ребята! Все ли у нас готово к уроку: вам понадобятся тетради, ручки, карандаши и линейки. У каждого из вас на парте лежат дополнительные материалы, которые понадобятся на уроке. |
||||||||||||||||||||||
|
Знакомство с темой урока. |
-Сегодня мы продолжаем цикл уроков по подготовке к ЕГЭ. Тема урока: Угол между двумя прямыми. |
||||||||||||||||||||||
|
Актуализация знаний |
-Давайте повторим случаи взаимного расположения прямых в пространстве. |
-пересекаются -параллельны -скрещиваются |
|||||||||||||||||||||
|
-А каково определение угла между двумя прямыми?
|
-Углом между двумя пересекающимися прямыми называется меньший из углов, образованных при пересечении прямых -Угол между параллельными прямыми равен 0; -Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельные данным скрещивающимся. |
||||||||||||||||||||||
|
-Помните ли вы формулу для нахождения угла между прямыми? |
Где a и b –длины сторон треугольника ABC. Соответственно параллельных этим прямым |
||||||||||||||||||||||
|
Решение задач: |
№1. (Для самостоятельного решения с последующим обсуждением для самопроверки) Доказать, что диагональ правильной четырехугольной призмы и не пересекающая ее диагональ основания взаимно перпендикулярны. |
D1 D B
A
Докажем, что D1B и AC перпендикулярны. D1D-перпендикуляр к плоскости основания. DB-проекция наклонной D1B на плоскость основания. DB и AC перпендикулярны так как ABCD-квадрат. Проведем прямую A’B’ через точку B параллельно прямой AC. Так как прямая A’B’ так же перпендикулярна DB, то по теореме о трех перпендикулярах A’C’ перпендикулярна прямой D1B. И, следовательно, AC перпендикулярна D1B. |
|||||||||||||||||||||
|
|
№2 Доказать, что непересекающиеся ребра правильной треугольной пирамиды взаимно перпендикулярны. |
S C B A S
O
Произведем
параллельный перенос прямой АС до пересечения с прямой SB. Проведем перпендикуляр из точки
В на сторону АС- отрезок BX . так как прямые A’C’ и AC параллельны, то ВX также перпендикулярен прямой A’C’. Отрезок SO-высота
пирамиды. О Тогда по теореме о трех перпендикулярах AC перпендикуляран SB. |
|||||||||||||||||||||
|
|
№3. (В обсуждении решения задачи участвует весь класс, учитель производит запись на доске) В кубе A…D1 найти угол между прямыми A1D и D1E, где E-середина ребра CC1
|
Решение. (Чертеж к задаче в Приложении 1 рис.1) Пусть ребро куба
равно 1, F- середина ребра BB1. Так как A1Fпараллельна D1E, то искомый угол φ- угол
при вершине A1 в треугольнике A1FD. Найдем стороны треугольника A1FD. Из треугольника BFD имеем:FD2=BD2+BF2=2+ Из треугольника A1B1F получаем: A1F2=A1B12+B1F2=1+ Из треугольника A1AD имеем: A1D2=A1A2+AD2=1+1=2 В треугольнике A1FD используем теорему косинусов: FD2-A1D2+A1F2-2A1D∙A1Fcosφ, Ответ: arccos
|
|||||||||||||||||||||
|
|
№4. (В обсуждении решения задачи участвует весь класс, учитель производит запись на доске)
В правильной треугольной призме ABCA1D1C1, все стороны которой равны, найти угол между прямыми AC1 и D1C |
Решение. (Чертеж к задаче в Приложении 1 рис.2)
cosφ= Ответ: arccos
|
|||||||||||||||||||||
|
|
№5 (Задача для самостоятельного решения с последующей проверкой)
В кубе A…D1 точки E и F-середины ребер A1B1 и B1C1 соответственно. Найдите косинус угла между прямыми AE и BF |
A1 A
Решение. Произведем параллельный перенос прямой BF до пересечения с прямой AE. Углом между прямой BF и AE будем считать угол F’AE. Найдем этот угол: AF’= F’E=
Ответ: 0,8
|
|||||||||||||||||||||
|
Домашнее задание |
В правильной шестиугольной призме A…F1. Все ребра которой равны, найдите косинус угла между прямыми AB1 и BC1 |
B’ B F
B1’ B1 A1
c
Пусть все ребра призмы имеют длину равную 1. Перенесем прямую AB1 до пересечения с прямой BC1 , получим прямую BB1 ‘ Тогда: BC1 2=BC2+CC1 2=1+1=2 (BB1 ‘)2=BB1 2+(B 1 B1 ‘)2=1+1=2 По теореме косинусов: (B 1 C 1 ‘)2=B1 C 1 2 =1+1-2 Найдем угол между прямыми:
Ответ: 0,75
|
|||||||||||||||||||||
Приложение 1 (плакат к уроку)
 |
|
|
D1 A1
E
B C
A
D
Рисунок 1
B1
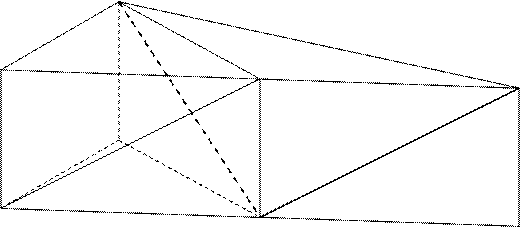 |
A1
M
B
A
N C C1
Рисунок 2
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.