Урок №1 по теме "Показательная функция, ее свойства и график" к главе 3 "Показательная и логарифмическая функции" учебника Мордковича А.Г. и др. Урок составлен в соответствии с деятельностным методом обучения, который является универсальным инструментом обучения. Предназначен для учащихся, которые владеют общими способами построения графиков элементарных функций.
Показательная функция, ее свойства и график.doc
Урок 1. Показательная функция, ее свойства и график.
Цели урока
1a или 0
: формировать умение строить графики показательных функций
y
1a ; развить умение читать графики функций, выделяя их свойства.
если
Ход урока:
x
a
,
I. Организационный момент.
Приветствие, сообщение темы и задач урока.
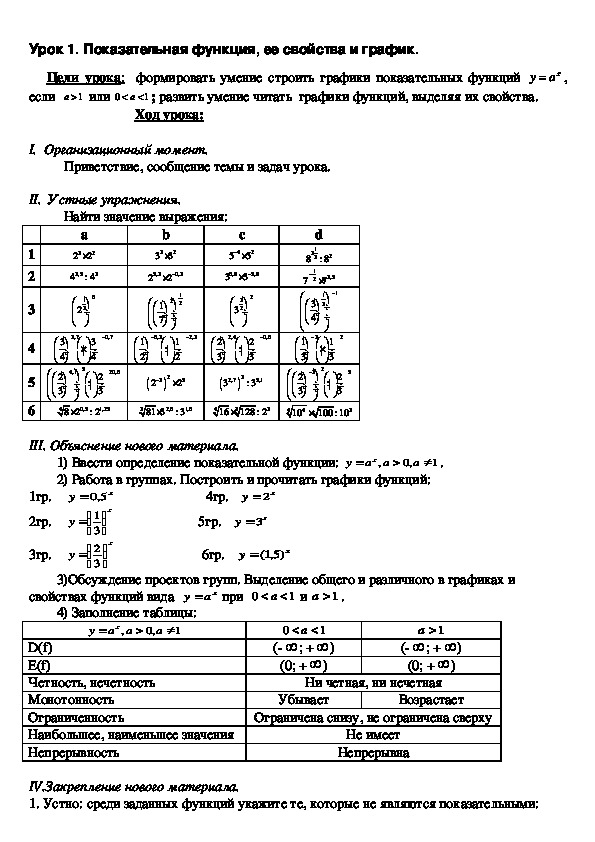
II. Устные упражнения.
Найти значение выражения:
a
2 2
3
2
3,5
4
3
: 4
6
1
32
b
3 3
3
2
5,3
2
0,3
2
1
2
1
7
2
c
5
4
2
5
6,8
3
3
5,8
2
3
23
0,7
3,7
3
4
3
4
5
2
3
4,1
2
:
3
20,6
2,3
6,3
1
2
1
:
2
2
23
5
2
2
3
0,6
2,4
2
:
3
2,7
3
5,1
: 3
3
d
2
1
2
38 : 8
1
7
27
1
33
4
3,5
1
1
3
3
2
1
3
5
2
2
3
3
2
:
3
4 8 2
0,5
1,25
: 2
3 81 3
2,6
1,6
: 3
4 16
3
128 : 2
3
4
4
10
100 :10
3
1
2
3
4
5
6
III. Объяснение нового материала.
1) Ввести определение показательной функции:
1
2) Работа в группах. Построить и прочитать графики функций:
1гр.
2гр.
4гр.
5гр.
аа
3
2
,0
а
y
y
y
y
y
x
x
,
x
x
.
5,0
1
3
2
3
x
x
y
6гр.
3гр.
3)Обсуждение проектов групп. Выделение общего и различного в графиках и
свойствах функций вида
0
4) Заполнение таблицы:
y при
)5,1(
1а
а
и
xа
1
y
.
x
y
x
аа
,
,0
а
1
D(f)
E(f)
Четность, нечетность
Монотонность
Ограниченность
Наибольшее, наименьшее значения
Непрерывность
а
0
1
( ; + )
(0; + )
1а
( ; + )
(0; + )
Ни четная, ни нечетная
Убывает
Возрастает
Ограничена снизу, не ограничена сверху
Не имеет
Непрерывна
IV.Закрепление нового материала.
1. Устно: среди заданных функций укажите те, которые не являются показательными:
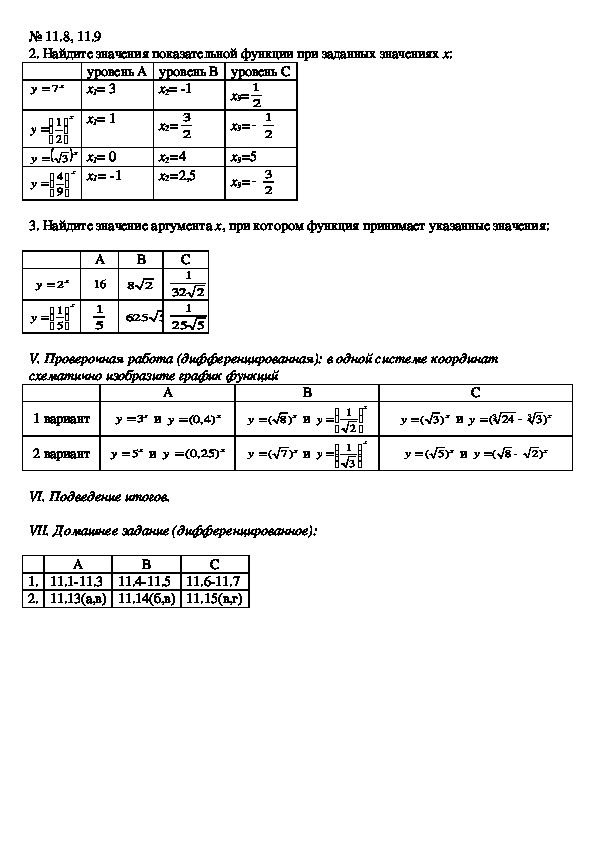
№ 11.8, 11.9
2. Найдите значения показательной функции при заданных значениях х:
уровень А уровень В уровень С
х1= 3
х2= 1
y
7
x
y
y
y
x
1
2
x
3
4
9
x
х1= 1
х1= 0
х1= 1
х2=
3
2
х2=4
х2=2,5
х3=
х3=
1
2
1
2
х3=5
х3=
3
2
3. Найдите значение аргумента x, при котором функция принимает указанные значения:
А
16
1
5
В
28
625
5
С
1
32
1
25
2
5
y
2
x
y
x
1
5
V. Проверочная работа (дифференцированная): в одной системе координат
схематично изобразите график функций
А
В
С
1 вариант
y
x
3 и
y
)4,0(
x
y
)8(
x
и
y
2 вариант
y
x
5 и
y
)25,0(
x
y
)7(
x
и
y
x
x
1
2
1
3
y
)3(
x
и
y
3
(
24
3
x
)3
y
)5(
x
и
y
8(
x
)2
VI. Подведение итогов.
VII. Домашнее задание (дифференцированное):
А
В
С
1. 11.111.3
11.611.7
2. 11.13(а,в) 11.14(б,в) 11.15(в,г)
11.411.5
Урок "Показательная функция, ее свойства и график".
Урок "Показательная функция, ее свойства и график".
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
01.07.2019
Посмотрите также:
© ООО «Знанио»
С вами с 2009 года.
О портале
