ВЕРОЯТНОСТЬ. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ

Филиал бюджетного образовательного учреждения Чувашской Республики

«Чебоксарский медицинский колледж»

Министерства здравоохранения Чувашской Республики в городе Канаш

                          

 

 

 

 

                

 

 

 

 

 

 

 

 

 

 

 

 

Методическая разработка

Пределы функции

ЕН.01. Математика

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Канаш, 2021

Цель урока: рассмотреть простейшие понятия теории вероятностей.

Задачи урока:

Обучающие:

Выработать умение решать задачи на определение классической вероятности с использованием основных формул;

научиться применять на практике понятия вероятности для решения профессиональных задач;

продемонстрировать важность изучаемой темы через связь с выбранной профессией.

способствовать запоминанию основной терминологии;

развивающие:

умения анализировать, систематизировать и обобщать полученные знания;

развитие навыков учащихся в вычислении классической вероятности;

формирование вероятностного мышления;

способствовать развитию интереса к математике; умений применять новый материал на практике и в жизни.

воспитательные

воспитать внимательность, исполнительность, добросовестность;

воспитывать графическую культуру;

   умение толерантно относиться друг к другу;

чувство ответственности за принятое решение.

Тип урока:

урок изучения нового материала

Вид урока:

комбинированный

Метод обучения:

репродуктивный, частично-поисковый.

Материально техническое оснащение урока:

компьютер, проектор, презентация по теме «Классическая вероятность событий», экран.

Методическая характеристика и особенности проведения урока:

Поскольку данный урок является уроком усвоения новых знаний, умений и навыков учащихся, то есть здесь в большой степени реализуется задача выработать умение решать задачи на определение классической вероятности с использованием основных формул; научиться применять на практике понятия вероятности для решения профессиональных задач; продемонстрировать важность изучаемой темы через связь с выбранной профессией; способствовать запоминанию основной терминологии:

Применяемые педагогические технологии:

·         использование мультимедиа в качества средства обучения (на всех этапах урока);

·         элементы поисковых технологий (постановка и решение проблемы поиска);

·         элементы развивающих технологий (формирование мотивации через профильность обучения математике, углубление интереса к предмету и выбранной профессии).

План урока:

1) Организационный момент.

2) Изучение нового материала.

2.1. Что изучает теория вероятностей.

2.2. Краткая историческая справка.

2.3. Что такое теория вероятностей?

2.4. Решение простейших задач у доски.

2.5. Решение задач в группах

3) Итоги урока.

4) Домашнее задание.

Ход урока

1. Организационный момент

Приветствие учеников, сообщение темы и цели урока

2. Повторение и закрепление пройденного материала

Ответы на вопросы по домашнему заданию (разбор нерешенных задач)

Многие вещи нам непонятны не потому, что наши понятия слабы;
но потому, что сии вещи не входят в круг наших понятий.
Козьма Прутков

Основная цель изучения математики в средних специальных учебных заведениях состоит в том, чтобы дать студентам набор математических знаний и навыков, необходимых для изучения других программных дисциплин, использующих в той или иной мере математику, для умения выполнять практические расчеты, для формирования и развития логического мышления.

В данной работе последовательно вводятся все базовые понятия раздела математики "Основы теории вероятностей и математической статистики", предусмотренные программой и Государственными образовательными стандартами среднего профессионального образования (Министерство образования Российской Федерации. М., 2002г.), формулируются основные теоремы, большая часть которых не доказывается. Рассматриваются основные задачи и методы их решения и технологии применения этих методов к решению практических задач. Изложение сопровождается подробными комментариями и многочисленными примерами.

Методические указания могут быть использованы для первичного ознакомления с изучаемым материалом, при конспектировании лекций, для подготовки к практическим занятиям, для закрепления полученных знаний, умений и навыков. Кроме того, пособие будет полезно и студентам- старшекурсникам как справочное пособие, позволяющее быстро восстановить в памяти то, что было изучено ранее.

В конце работы приведены примеры и задания, которые студенты могут выполнять в режиме самоконтроля.

Методические указания предназначены для студентов заочной и дневной форм обучения.

I. ВЕРОЯТНОСТЬ. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ

1.1. Основные понятия комбинаторики

В разделе математики, который называется комбинаторикой, решаются некоторые задачи, связанные с рассмотрением множеств и составлением различных комбинаций из элементов этих множеств. Например, если взять 10 различных цифр 0, 1, 2, 3,: , 9 и составлять из них комбинации, то будем получать различные числа, например 143, 431, 5671, 1207, 43 и т.п.

Мы видим, что некоторые из таких комбинаций отличаются только порядком цифр (например, 143 и 431), другие - входящими в них цифрами (например, 5671 и 1207), третьи различаются и числом цифр (например, 143 и 43).

Таким образом, полученные комбинации удовлетворяют различным условиям.

В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.

Предварительно познакомимся с понятием факториала.

Произведение всех натуральных чисел от 1 до n включительно называют n-факториалом и пишут .

Пример 1.

Вычислить: а) ; б) ; в) .

Решение. а) .

б) Так как  и , то можно вынести за скобки 

Тогда получим

.

в) .

Перестановки.

Комбинация из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками.

Перестановки обозначаются символом Р_n, где n- число элементов, входящих в каждую перестановку. (Р - первая буква французского слова permutation- перестановка).

Число перестановок можно вычислить по формуле

или с помощью факториала:

Запомним, что 0!=1 и 1!=1.

Пример 2. Сколькими способами можно расставлять на одной полке шесть различных книг?

Решение. Искомое число способов равно числу перестановок из 6 элементов, т.е.

.

Размещения.

Размещениями из m элементов в n в каждом называются такие соединения, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком из расположения.

Размещения обозначаются символом , где m- число всех имеющихся элементов, n- число элементов в каждой комбинации. (А-первая буква французского слова arrangement, что означает "размещение, приведение в порядок").

При этом полагают, что nm.

Число размещений можно вычислить по формуле

,

т.е. число всех возможных размещений из m элементов по n равно произведению n последовательных целых чисел, из которых большее есть m.

Запишем эту формулу в факториальной форме:

.

Пример 3. Сколько вариантов распределения трех путевок в санатории различного профиля можно составить для пяти претендентов?

Решение. Искомое число вариантов равно числу размещений из 5 элементов по 3 элемента, т.е.

.

Сочетания.

Сочетаниями называются все возможные комбинации из m элементов по n, которые отличаются друг от друга по крайней мере хотя бы одним элементом (здесь m и n-натуральные числа, причем n  m).

Число сочетаний из m элементов по n обозначаются  (С-первая буква французского слова combination - сочетание).

В общем случае число из m элементов по n равно числу размещений из m элементов по n, деленному на число перестановок из n элементов:

Используя для чисел размещений и перестановок факториальные формулы, получим:

Пример 4. В бригаде из 25 человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать?

Решение. Так как порядок выбранных четырех человек не имеет значения, то это можно сделать  способами.

Находим по первой формуле

.

Кроме того, при решении задач используются следующие формулы, выражающие основные свойства сочетаний:

 

(по определению полагают  и );

.

1.2. Решение комбинаторных задач

Задача 1. На факультете изучается 16 предметов. На понедельник нужно в расписание поставить 3 предмета. Сколькими способами можно это сделать?

Решение. Способов постановки в расписание трех предметов из 16 столько, сколько можно составить размещений из 16 элементов по 3.

.

Задача 2. Из 15 объектов нужно отобрать 10 объектов. Сколькими способами это можно сделать?

Решение.

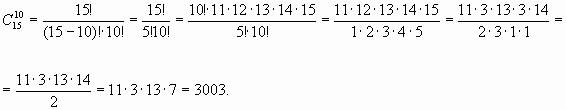
Задача 3. В соревнованиях участвовало четыре команды. Сколько вариантов распределения мест между ними возможно?

Решение.

.

Задача 4. Сколькими способами можно составить дозор из трех солдат и одного офицера, если имеется 80 солдат и 3 офицера?

Решение. Солдат в дозор можно выбрать

способами, а офицеров  способами. Так как с каждой командой из солдат может пойти любой офицер, то всего имеется  способов.

Задача 5. Найти , если известно, что .

Решение.

Так как , то получим

,

,

,

, .

По определению сочетания следует, что , . Т.о. .

Ответ: 9

1.3. Понятие о случайном событии. Виды событий. Вероятность события

Всякое действие, явление, наблюдение с несколькими различными исходами, реализуемое при данном комплексе условий, будем называть испытанием.

Результат этого действия или наблюдения называется событием.

Если событие при заданных условиях может произойти или не произойти, то оно называется случайным. В том случае, когда событие должно непременно произойти, его называют достоверным, а в том случае, когда оно заведомо не может произойти,- невозможным.

События называются несовместными, если каждый раз возможно появление только одного из них.

События называются совместными, если в данных условиях появление одного из этих событий не исключает появление другого при том же испытании.

События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны.

События принято обозначать заглавными буквами латинского алфавита: А, В, С, Д, : .

Полной системой событий А₁, А₂, А₃, : , А_n называется совокупность несовместных событий, наступление хотя бы одного из которых обязательно при данном испытании.

Если полная система состоит из двух несовместных событий, то такие события называются противоположными и обозначаются А и .

Пример. В коробке находится 30 пронумерованных шаров. Установить, какие из следующих событий являются невозможными, достоверными, противоположными:

достали пронумерованный шар (А);

достали шар с четным номером (В);

достали шар с нечетным номером (С);

достали шар без номера (Д).

Какие из них образуют полную группу?

Решение. А - достоверное событие; Д - невозможное событие;

В и С - противоположные события.

Полную группу событий составляют А и Д, В и С.

Вероятность события, рассматривается как мера объективной возможности появления случайного события.

1.4. Классическое определение вероятности

Число, являющееся выражением меры объективной возможности наступления события, называется вероятностью этого события и обозначается символом Р(А).

Определение. Вероятностью события А называется отношение числа исходов m, благоприятствующих наступлению данного события А, к числу n всех исходов (несовместных, единственно возможных и равновозможных), т.е. .

Следовательно, для нахождения вероятности события необходимо, рассмотрев различные исходы испытания, подсчитать все возможные несовместные исходы n, выбрать число интересующих нас исходов m и вычислить отношение m к n.

Из этого определения вытекают следующие свойства:

Вероятность любого испытания есть неотрицательное число, не превосходящее единицы.

Действительно, число m искомых событий заключено в пределах . Разделив обе части на n, получим

.

2. Вероятность достоверного события равна единице, т.к. .

3. Вероятность невозможного события равна нулю, поскольку .

Задача 1. В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?

Решение. Общее число различных исходов есть n=1000. Число исходов, благоприятствующих получению выигрыша, составляет m=200. Согласно формуле, получим

.

Задача 2. В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. Найти вероятность того, что из этих 5 деталей две окажутся бракованными.

Решение. Число всех равновозможных независимых исходов n равно числу сочетаний из 18 по 5 т.е.

Подсчитаем число m, благоприятствующих событию А. Среди 5 взятых наугад деталей должно быть 3 качественных и 2 бракованных. Число способов выборки двух бракованных деталей из 4 имеющихся бракованных равно числу сочетаний из 4 по 2:

.

Число способов выборки трех качественных деталей из 14 имеющихся качественных равно

.

Любая группа качественных деталей может комбинироваться с любой группой бракованных деталей, поэтому общее число комбинаций m составляет

.

Искомая вероятность события А равна отношению числа исходов m, благоприятствующих этому событию, к числу n всех равновозможных независимых исходов:

.

1.5. Теорема сложения вероятностей несовместных событий

Суммой конечного числа событий называется событие, состоящее в наступлении хотя бы одного из них.

Сумму двух событий обозначают символом А+В, а сумму n событий символом А₁+А₂+ : +А_n.

Теорема сложения вероятностей.

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.

 или

Следствие 1. Если событие А₁, А₂, : ,А_n образуют полную систему, то сумма вероятностей этих событий равна единице.

.

Следствие 2. Сумма вероятностей противоположных событий  и  равна единице.

.

Задача 1. Имеется 100 лотерейных билетов. Известно, что на 5 билетов попадает выигрыш по 20000 руб., на 10 - по 15000 руб, на 15 - по 10000 руб., на 25 - по 2000 руб. и на остальные ничего. Найти вероятность того, что на купленный билет будет получен выигрыш не менее 10000 руб.

Решение. Пусть А, В, и С- события, состоящие в том, что на купленный билет падает выигрыш, равный соответственно 20000, 15000 и 10000 руб. так как события А, В и С несовместны, то

.

Задача 2. На заочное отделение техникума поступают контрольные работы по математике из городов А, В и С. Вероятность поступления контрольной работы из города А равна 0,6, из города В - 0,1. Найти вероятность того, что очередная контрольная работа поступит из города С.

Решение. События "контрольная работа поступила из города А", "контрольная работа поступила из города В" и "контрольная работа поступила из города С" образуют полную систему, поэтому сумма их вероятностей равна единице:

, т.е. .

Задача 3. Вероятность того, что день будет ясным, . Найти вероятность  того, что день будет облачным.

Решение. События "день ясный" и "день облачный" противоположные, поэтому

, т.е .

1.6. Теорема умножения вероятностей независимых событий

При совместном рассмотрении двух случайных событий А и В возникает вопрос:

Как связаны события А и В друг с другом, как наступление одного из них влияет на возможность наступления другого?

Простейшим примером связи между двумя событиями служит причинная связь, когда наступление одного из событий обязательно приводит к наступлению другого, или наоборот, когда наступление одного исключает возможность наступления другого.

Для характеристики зависимости одних событий от других вводится понятие условной вероятности.

Определение. Пусть А и В - два случайных события одного и того же испытания. Тогда условной вероятностью события А или вероятностью события А при условии, что наступило событие В, называется число .

Обозначив условную вероятность , получим формулу

, .

Задача 1. Вычислить вероятность того, что в семье, где есть один ребенок- мальчик, родится второй мальчик.

Решение. Пусть событие А состоит в том, что в семье два мальчика, а событие В - что один мальчик.

Рассмотрим все возможные исходы: мальчик и мальчик; мальчик и девочка; девочка и мальчик; девочка и девочка.

Тогда ,  и по формуле находим

.

Событие А называется независимым от события В, если наступление события В не оказывает никакого влияния на вероятность наступления события А.

Теорема умножения вероятностей

Вероятность одновременного появления двух независимых событий равна произведению вероятностей этих событий:

.

Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле

.

Задача 2. В первой урне находится 6 черных и 4 белых шара, во второй- 5 черных и 7 белых шаров. Из каждой урны извлекают по одному шару. Какова вероятность того, что оба шара окажутся белыми.

Решение. Пусть  - из первой урны извлечен белый шар; - из второй урны извлечен белый шар. Очевидно, что события  и  независимы.

Так как , , то по формуле  находим

.

Задача 3. Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента равна 0,2; вероятность выхода из строя второго элемента равна 0,3. Найти вероятность того, что: а) оба элемента выйдут из строя; б) оба элемента будут работать.

Решение. Пусть событие А- выход из строя первого элемента, событие В- выход их строя второго элемента. Эти события независимы (по условию).

а) Одновременное появление А и В есть событие АВ. Следовательно,

.

б) Если работает первый элемент, то имеет место событие  (противоположное событию А- выходу этого элемента из строя); если работает второй элемент- событие В. Найдем вероятности событий  и :

;

.

Тогда событие, состоящее в том, что будут работать оба элемента, есть  и, значит,

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тип урока:

Семинарское занятие.

Вид урока:

комбинированный

Метод обучения:

репродуктивный, частично-поисковый.

Материально техническое оснащение урока:

компьютер, проектор, презентация по теме «Элементы теории вероятностей. Комбинаторика.

Применяемые педагогические технологии:

·         использование мультимедиа в качества средства обучения (на всех этапах урока);

·         элементы поисковых технологий (постановка и решение проблемы поиска);

·         элементы развивающих технологий (формирование мотивации через профильность обучения математике, углубление интереса к предмету и выбранной профессии).

План урока:

1) Организационный момент.

2) Повторение и закрепление пройденного материала.

3) Изучение нового материала.

3.1. Что изучает теория вероятностей.

3.2. Краткая историческая справка.

3.3. Что такое теория вероятностей?

3.4. Решение простейших задач у доски.

3.5. Решение задач в группах

4) Итоги урока.

5) Домашнее задание.

Ход урока

1. Организационный момент

Приветствие учеников, сообщение темы и цели урока

2. Повторение и закрепление пройденного материала

Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

1.    Изучение нового материала

3.1. Что изучает теория вероятностей.

Теория вероятностей – это раздел математической науки, изучающий закономерности случайных явлений. Предметом изучения теории вероятностей является исследование вероятностных закономерностей случайных (однородных) массовых явлений. Методы, выявленные в теории вероятностей, нашли широкое применение в большинстве современных наук и различных отраслях деятельности человека.

3.2. Краткая историческая справка

Как наука теория вероятности зародилась в 17в. Появление понятия вероятности было связано как с ᴨᴏᴛребностями страхования, получившего значительное распростᴘẚʜᴇние в ту эпоху, когда заметно росли торговые связи и морские путешествия, так и в связи с запросами азартных игр.

Схема азартных игр была очень проста и могла быть подвергнута всестороннему логическому анализу. Первые попытки этого рода связаны с именами известных учёных – алгебраиста Джероламо Кардано (1501 – 1576) и Галилео Галилея (1564 – 1642). Но при этом честь открытия этой теории, которая не только предоставляет возможность сравнивать случайные величины, но и производить определенные математические операции с ними, принадлежит двум выдающимися ученым – Блезу Паскалю (1623 – 1662) и Пьеру Ферма. Ещё в древности было замечено, что имеются явления, которые обладают особенностью: при малом числе наблюдений над ними не наблюдается никакой правильности, но по мере увеличения числа наблюдений всё яснее проявляется определенная закономерность. 

Во второй половине XIX века основной вклад внесли русские учёные П. Л. Чебышев, А. А. Марков и А. М. Ляпунов. В это время были доказаны закон больших чисел, центральная предельная теорема, а кроме того разработана теория цепей Маркова. Современный̆ вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем Колмогоровым.

Первичные понятия теории вероятностей:  
В теории вероятностей рассматривается следующая модель изучаемых явлений реальной жизни: проводится опыт (испытание), в результате происходят случайные события (обычно говорят короче – события).

Например, бросают монету и смотрят, какая ее сторона оказалась сверху. В результате этого опыта может выпасть орел – это одно событие, а может выпасть решка– это другое событие. Поскольку выпадение орла зависит от случая, то это случайное событие.

Итак, дадим определение первичных понятий теории вероятностей. 

Опыт (испытание) – это производимые действия. 

Событие – это результат опыта.

Какое-либо конкретное событие является, как правило, делом случая (оно может произойти, а может и не произойти) и поэтому оно называется случайным.

Пример.

Стрелок стреляет по мишени, разделенной на четыре области. Выстрел – это испытание. Попадание в определенную область мишени – событие. В урне имеются цветные шары. Из урны наудачу берут один шар. Извлечение шара из урны есть испытание. Появление шара определенного цвета – событие.

В жизни мы постоянно сталкиваемся с тем, что некоторое событие может произойти, а может и не произойти.

Например:

В 12.00 по мосту проедет красная машина. Перед машиной пробежит черная кошка. При бросании кубика выпадет тройка.

Такие непредсказуемые события называются случайными.

Теория вероятностей изучает различные модели случайных событий, их свойства и характеристики. Разумеется, эта теория не может однозначно предсказать, какое событие в реальности произойдет, но может оценить, какое событие наиболее вероятно. При этом будем считать, что случайные события равновероятные (или равновозможные), - идеализированная модель.

Два события, которые в данных условиях могут происходить одновременно, называются совместными, а те, которые не могут происходить одновременно, - несовместными. 

Примеры.

1. Из ящика с деталями наудачу извлечена деталь. Появление стандартной детали исключает появление нестандартной детали. События «появилась стандартная деталь» и «появилась нестандартная деталь» - несовместные.

2. Брошена монета. Появление орла исключает появление решки. События «появился орел» и «появилась решка» - несовместные.

3. Примеры ребят.

Равновозможными называются события, когда в их наступлении нет преимуществ. 

Неравновозможные события те, у которых в наступлении одного из событий есть какое- то преимущество.

Примеры.

1. Появление орла или решки при бросании монеты представляют собой равновероятные события.

2. Пусть бросают игральную кость. В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно).

3. Примеры ребят.

Событие, которое происходит всегда, называют достоверным событием.

Вероятность достоверного события равна 1.

Событие, которое не может произойти, называется невозможным.

Вероятность невозможного события равна 0.

Примеры.

1. Машина заведется без аккумулятора. При бросании кубика выпадет семерка. Это невозможные события.

2. Машина заведется с аккумулятором. При бросании кубика выпадет число, меньше семи. Это достоверные события.

3. Пусть, например, в автосалоне продаются только белые автомобили, продают один. Тогда продажа белого автомобиля – достоверное событие; продажа черного автомобиля – невозможное событие.

4. Приведите примеры достоверных и невозможных событий.

3.3. Что такое «теория вероятностей»? 

Теория вероятностей – раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. (Советский энциклопедический словарь, 1982 год)

·         Теория вероятностей – это математическая наука, позволяющая по вероятностям одних случайных событий находить вероятности других случайных событий, связанных каким – либо образом с первыми. (А.А.Боровков «Теория вероятностей», М.: Наука, 1986 год.)

·         Вероятность – это численная характеристика реальности появления того или иного события.

Классическое определение вероятности. 

Вероятностью события А при проведении некоторого испытания называют отношение числа тех исходов, в результате которых наступает событие А, к общему числу всех (равновозможных между собой) исходов этого испытания.

Для решения задач используют алгоритм нахождения вероятности случайного события.

Для нахождения вероятности случайного события А при проведении некоторого испытания следует найти:

1) число N всех возможных исходов данного испытания;

2) количество N(A) тех исходов, в которых наступает событие А;

3) частное N(A)/ N, оно и будет равно вероятности события А.

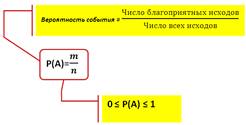
Принято вероятность события А обозначать так: Р(А).

Значит Р(А)= N(A)/ N

Примеры.

1.    На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность Р(А) того, что взятый наудачу подшипник окажется стандартным.

Решение. Число стандартных подшипников равно 1000 – 30 = 970. Будем считать, что каждый подшипник имеет одинаковую вероятность быть выбранным. Тогда полная группа событий состоит из N = 1000 равновероятных исходов, из которых событию А благоприятствуют N(A) = 970 исходов.

Поэтому Р(А) = 

Ответ: 0,97.

Для вычисления вероятности часто используют правило умножения. (слайд 16)

Для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.

Пример.

Найдем вероятность того, что при подбрасывании двух костей суммарное число очков окажется равным 5.

Решение. Возможно следующее сочетание очков на первой и второй костях:

1 + 4, 2 + 3, 3 + 2, 4 + 1 – четыре благоприятных случая (N(A) = 4). Всего возможных исходов N = 6·6 = 36 (по шесть для каждой кости). Тогда вероятность рассматриваемого события 

Ответ: .

Вероятность Р(А) некоторого события .

При решении некоторых задач удобно использовать свойство вероятностей противоположных событий. (слайд 17)

События А и В называются противоположными, если всякое наступление события А означает не наступление события В, а не наступление события А – наступление события В.

Событие, противоположное событию А, обозначают символом . Сумма вероятностей противоположных событий равна 1. .

Пример. (слайд 18)

В среднем из 1000 аккумуляторов, поступивших в продажу, 6 неисправны. Найдите вероятность того, что один купленный аккумулятор окажется исправным.

Решение. Элементарный исход – случайно выбранный аккумулятор. Поэтому

N = 1000.

Событию А = {аккумулятор исправен} благоприятствуют 1000 – 6 = 994 исхода.

Поэтому N(A) = 994.

Тогда 

Ответ: 0,994.

Эту задачу можно решить с помощью формулы вероятности противоположного события  = {аккумулятор неисправен}. Тогда N(Ā)=6.

Имеем =  Значит, P(A) = 1- =1 – 0,006 = 0,994.

Ответ: 0,994.

3.4. Решение задач у доски. (слайд 19)

1.  Автомобиль проезжает мимо светофора два раза, какова вероятность того что: хотя бы один раз, будет гореть зеленый?:
а) хотя бы один раз, будет гореть зеленый? б) оба раза, будет гореть зеленый?

Решение. а) Пусть А - событие, состоящее в том, что в результате проведенного испытания хотя бы один раз, будет гореть зеленый?
Равновозможными элементарными исходами здесь являются: КЗ, КЖ, КК, ЗК, ЗЖ, ЗЗ, ЖК, ЖЗ, ЖЖ, т.е. N = 9. Событию А благоприятствуют исходы: КЗ,ЗК, ЗЖ, ЗЗ, ЖЗ, т.е. N(A) = 5.
Следовательно, 
б) Пусть В - событие, состоящее в том, что в результате проведенного испытания оба раза, будет гореть зеленый.
Событию В благоприятствует один исход ЗЗ, т.е. N(B) = 1. Следовательно, 

Ответ: а) ; б) .

2.  У Маши сломался автомобиль, она набирает номер автосервиса, но понимает, что забыла последнюю цифру номера телефона, найдите вероятность того, что девушка дозвонится до мастера с первого раза? (слайд 20)

Решение. Общее число элементарных исходов равно N = 10 .
Событию А благоприятствует одна цифра,  N(А) = 1.
Следовательно, .

Ответ: .

3. В фирме такси 6 красных и 6 желтых автомобилей. На вызов уехало 8 машин. Определите вероятность события А - все выбранные машины красные. (слайд 21)

Решение. Р(А) = 0, т.к. это событие А - невозможное.

Ответ: 0.

4. Научная конференция проводится 3 дня. Всего запланировано 50 докладов: в первый день – 30 докладов, а остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьевкой. Какова вероятность, что доклад автомеханике окажется запланированным на последний день конференции? (слайд 22)

Решение. Так как в третий день будут слушать 10 докладов, то благоприятных исходов N(А) = 10, а всего докладов 50, т.е. равновозможных исходов N = 50. Поэтому .

Ответ: 0,2.

5. Перед началом первого тура чемпионата по автогонкам разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 51 гонщиков, среди которых 16 участников из России, в том числе Василий Петров. Найдите вероятность того, что в первом туре Василий Петров будет соревноваться с каким – либо гонщиком из России. (слайд 23)

Решение. Число всех исходов N = 50. Число элементарных событий, благоприятствующих событию А равно 15. Все элементарные события равновозможные по условию задачи, поэтому 

Ответ: 0,3.

3.5. Решение задач в группах (слайд 24)

А теперь перейдем к работе в группах. Ученики делятся на 3группы. Ваша задача: решить задачи, оформить их в тетрадях и рассказать о проделанной совместной работе. Листочки с заданиями на столах. Помогайте друг другу при решении. (Учитель, в процессе работы учащихся, оказывает помощь каждой группе).

Задачи:

1. В двигатели автомобиля 4 свечи зажигания, какова вероятность того, что одна из них вышла из строя.

2. В автосервисе стоят 6 поломанных автомобилей: 1- ГАЗ, 2- ВАЗ (LADA), 1- УАЗ, 1 - Ford,1- Chevrolet. Найдите вероятность того, что первыми сделают иномарки.

3. В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет 8 очков.

4. На экзамене по автомеханике в 4 билетах встречается вопрос про трансмиссию, 7 билетов про двигатель, 9 билетов про ходовую часть и 5- про электрооборудование. Студент выучил все билеты про ходовую часть автомобиля. Найдите вероятность того, что билет, который он вытянет, окажется про ходовую часть автомобиля.

5. В чемпионате России по автогонкам участвует 20 спортсменов: 8 из Южного ФО, 7 из Центрального ФО, остальные – из Северо-Западный ФО. Порядок, в котором выступают гонщики, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из Северо-Западный ФО.

6. Фабрика выпускает шины на автомобиль. В среднем на 100 качественных шин приходится восемь шин со скрытыми дефектами. Найдите вероятность того, что купленная шина окажется качественной. Результат округлите до сотых.

Решения к задачам (слайд 25)

1. Общее число элементарных событий N = 4. Событию A = {одна свеча вышла из строя}

благоприятствует только одно элементарное событие. Поэтому N(A)=1.

Тогда .

Ответ: 0,25.

2. Автомобилей всего шесть. Значит, N=6. Событию A={сделают иномарку} благоприятствует два элементарных события: Ford, Chevrolet. Поэтому N(A) = 2. Элементарные события равновозможные. Поэтому .

Ответ: .

3.Элементарный исход в этом опыте – порядочная пара чисел. Первое число выпадает на первом кубике, а второе – на втором. Множество элементарных исходов удобно представить таблицей. Строки соответствуют результату первого броска, столбцы – результату второго броска. Всего элементарных событий N = 3. (слайд 26)

1 2 3 4 5 6

1

2

3

4

5

6

2

3

4

5

6

7

3

4

5

6

7

8

4

5

6

7

8

9

5

6

7

8

9

10

6

7

8

9

10

11

7

8

9

10

11

12

Напишем в каждой клетке таблицы сумму выпавших очков и закрасим клетки где сумма равна 8. Таких ячеек 5. Значит событию А = {сумма равна 8} благоприятствует пять элементарных исходов. Следовательно, N(A) = 5.

Поэтому 

Ответ: 

(слайд 27)

4. Всего билетов N=4+7+9+5+5=25. Событию А = {билет про ходовую часть} благоприятствуют только 9 исходов. Поэтому N(A)=9.

Тогда 

Ответ: 0,36.

5. Элементарные события – спортсмен, выступающий первым. Поэтому N=20. Чтобы найти число элементарных событий, благоприятствующих событию А = {первым выступит спортсмен из Северо-Западный ФО }, нужно подсчитать число спортсменов из Северо-Западный ФО: N(A)=20-(8+7)=5. Все элементарные события равновозможные по условию задачи, поэтому 

Ответ: 0,25.

6. Элементарный исход – случайно выбранная шина. Поэтому N = 108.

Событию А = {качественная шина} благоприятствуют 100 исходов.

Поэтому N(A) = 100.

Тогда 

Ответ: 0,93.

Отчет групп о проделанной работе

4. Итоги урока (слайд 28)

Ученики проговаривают, что нового узнали на уроке. Учитель оценивает работу ребят. При выходе из кабинета каждый ученик выбирает прямоугольник по цвету, соответствующему надписями «всё понятно и усвоено», «трудно и не понятно», и опускает в соответствующий конверт.

5. Домашнее задание

Придумать 5 задач, связанных с профессией автомеханик, на нахождение классической вероятности.

 

 

 

Список литературы

1. А.Г.Мордкович. Алгебра и начала математического анализа.

10 - 11классы. В 2 ч. Ч. 1. Учебник;

2. А.Г.Мордкович и др. Алгебра и начала математического анализа.

10 – 11классы. В 2 ч. Ч. 2. Задачник;

 

Скачано с www.znanio.ru