Введение понятия производной в средней школе

Введение понятия производной в средней школе

При изучении темы "Производная" проявляются известные трудности, связанные с осуществлением предельных переходов. Важно поэтому придать изложению возможно более наглядный и конкретный характер.

Включённые в курс сведения о пределах имеют вспомогательный характер, они не обходимы для вывода формул производных. Основное внимание должно быть уделено не формальному применению теорем о пределах, а сознательному проведению предельных переходов для приближённого вычисления значений конкретных функций и их приращений. Многочлены невысоких степеней и их частных -наиболее простой объект для иллюстрации идеи предельного перехода.

Определению производной функции как предела разностного отношения предшествует рассмотрению особенностей поведения графиков гладких функций, приводящее к понятию касательной. Производная функции появляется сначала как тангенс угла наклона касательной к оси абсцисс. Тем самым с понятием производной на первом этапе связывается наглядный образ – касательная. Предельные переходы появляются как средство вычисления производной.

Различные подходы к введению производной определяются логической связью этого понятия с более общим понятием предела функции в точке.

Логический подход при введении производной в качестве базисного понятия использует определение предела функции в точке. Так в учебных программах по математике 1968 года, используя этот подход, определяли это понятие: 1) исходя из арифметического толкования предела функции (определение по Коши или на языке абсолютной погрешности):

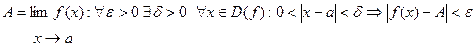
2) исходя из операции предела функции в точке через окрестности (топологическое): a- предельная точка множества E, т.е.

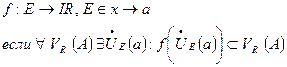
В действующих школьных программах по математике при введении производной функции используют исторический подход, т.е. первоначально формируются понятия производной, и только затем, как обобщение, понятие предела функции. При таком подходе большое внимание уделяется практическим аспектам изучения производной.