Вычисление и сравнение логарифмов. Решение логарифмических уравнений

 

 

 

 

 

 

 

 

 

Методическая разработка

практического занятия для студента

Тема: «Вычисление и сравнение логарифмов. Решение логарифмических уравнений»

 

ОУП. 04 «МАТЕМАТИКА»

 

Специальность 34.02.01 «Сестринское дело»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ТЕМА: «ВЫЧИСЛЕНИЕ И СРАВНЕНИЕ ЛОГАРИФМОВ. РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ»

1.     Тип занятия: практическое.

2.     Место проведения, продолжительность занятия: учебная аудитория, 90 минут

3.     Цели занятия для студентов: показать свои знания, умения и навыки по применению определения логарифма и его свойств, закрепить навыки решения логарифмических уравнений 

4.     Требования к уровню освоения дидактических единиц:

В результате студент должен:

-Знать определение логарифма числа, свойства логарифмов.

-Знать понятие степени с действительным показателем и ее свойства.

- Знать способы решения логарифмических уравнений

-Уметь правильно пользоваться математической символикой в процессе выполнения заданий.

-Уметь выполнять преобразование выражений, применяя формулы, связанные со свойствами степеней, логарифмов.

5.     Оснащение занятия: Алимов Ш. А., Колягин Ю. М. «Алгебра  и начала математического анализа», доска, мел, тетради с конспектами, карточки с заданиями для практической работы, карточки со справочным материалом.

6.     Деятельность студентов в ходе занятия

6.1         Выполните следующие задания у доски с целью проверки домашнего задания

Вариант

1.   

2.  

3.  

4.   

5.  

6.  

7.  

8.  

9.  

10.  

11.

12.  

13.   

14.  

15.  

 

6.2         Прослушайте инструктаж по выполнению практической работы, возьмите справочный материал и карточки с заданиями

Инструктаж студентов по выполнению практических заданий

Задания необходимо оформить в тетрадях для практических работ. Выполнить индивидуальную работу по варианту. Вариант содержит необходимый справочный материал.  На выполнение задания отводится 60 минут. В конце работы необходимо написать вывод. В конце занятия необходимо сдать тетради для проверки и оценивания.

Справочный материал

Опр.

Логарифмом числа b по основанию а, где  а > 0 , а ≠ 1, называется показатель степени, в которую надо возвести число а, чтобы получить число b.

Примеры

1.  

2.  

Определение логарифма можно записать так  .  Его называют основным логарифмическим тождеством.

При преобразовании и вычислении значений логарифмических выражений применяют свойства логарифмов.

Свойства

 

1.  

2.  

3.  

4.  

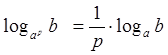
Формула перехода к другому основанию: 

Опр.

Десятичным логарифмом числа называют логарифм этого числа по основанию 10 и пишут lg b вместо log₁₀ b

   log₁₀ b= lg b

Опр.

Натуральным логарифмом числа называют логарифм этого числа по основанию е, где е  -  иррациональное число, приближённо равное 2,7. При этом пишут ln b   вместо    log_e b, т.е.  log_e b = ln b 

Действие нахождения логарифма числа называется логарифмированием.

Действие, обратное логарифмированию называется потенцированием.

Уравнения, содержащие неизвестное под знаком логарифма, называются логарифмическими.

Такие уравнения решаются с помощью определения логарифма, теорем о логарифмах и утверждения, что если положительные числа равны, то и равны их логарифмы при данном основании и обратно, если логарифмы чисел равны, то равны и соответствующие им числа. Во всех случаях полученные решения необходимо проверить подстановкой их в данное уравнение и исключить посторонний

 

6.3         Самостоятельно выполните задания из практической работы № 5

Тема: «Вычисление и сравнение логарифмов. Решение логарифмических уравнений»

Цель: показать свои знания, умения и навыки по применению определения логарифма и его свойств, закрепить навыки решения логарифмических уравнений

Вариант 1

1. Вычислите    А)

В) 

3. Вычислите    А)     Б)

4.Вычислите:

А)      Б)     В)

Г)     Д)  

5. Решить уравнения

А)                  

Б) 

В)

Вариант 2.

1.Вычислите А)

 В)

3. Найдите: А)          Б)   

4. Вычислите:

А)      Б)     В)

Г)     Д)   

5. Решить уравнения

А)                  

Б)  

В)

 

Критерии оценивания практической работы.

 

Отметка «5» ставится, если студент:

 работа выполнена полностью;

 в логических рассуждениях и обосновании решения нет пробелов и ошибок;

 в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится, если студент:

 работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

 допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если студент:

 допущено более одной ошибки или более двух – трех недочетов в выкладках,

чертежах или графиках, но учащийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если студент:

 допущены существенные ошибки, показавшие, что учащийся не обладает

обязательными умениями по данной теме в полной мере.

6.4         Запишите домашнее задание в тетрадь

Ознакомьтесь  с презентацией: «Изображение пространственных фигур» и заполните таблицу.

Название фигуры	Определение фигуры	Изображение фигуры
Прямоугольный параллелепипед
Куб
Тетраэдр
Четырехугольная пирамида
Пятиугольная пирамида
Шестиугольная пирамида
Треугольная призма
Четырехугольная призма
Пятиугольная призма
Шестиугольная призма
Цилиндр
Конус
Шар

 

6.5         Рефлексия

Оцените свою деятельность и заполните таблицу

Утверждения	«+» или «-», перечисление ошибок, темы для доработки.
1) У меня сегодня всё получалось, я не допускал ошибок
2) Я допустил ошибки в самостоятельной работе (перечислить ошибки)
3) Я исправил допущенные ошибки в процессе работы над ними
4) Мне необходимо поработать над…