Вычисление расстояния в пространстве.

Урок – практикум по теме «Вычисление расстояний в пространстве».    

Тема:

         Вычисление расстояния в пространстве.

Цели урока:

1)     Образовательные: закрепление пройденного материала,

2)     Воспитательные: уметь анализировать, сопоставлять алгоритмы вычисления, делать соответствующие выводы, уметь работать в группе.

3)     Развивающие: отработка построения чертежей в пространстве, выполнение дополнительных построений.

       Оборудование: мультимедийный проектор, экран.

Технологии: информационно – коммуникационный технологии, работа в группах.

             Эпиграф: «Умение решать разнообразные задачи, остроумие, необходимое для этого, приобретаются упорством и практикой рассуждения» Карл Гаусс.

Ход урока:

1)     Устный опрос

2)     Работа по готовым чертежам

3)     Практикум по решению задач

4)     Подведение итогов урока.

            Задачи для устного опроса (решают во время разминки).

                          Разминка – «дальше-дальше».

-        угол ромба равен 30, высота 10. Найти S_p                                           (200)

-        S поверхности всего куба равна 24 см² .V =  ?                      (8 см³)

-        всегда ли можно провести плоскость через прямую и две точки вне этой прямой?                                                                       (не всегда)

-        четыре точки не лежат в одной плоскости. Могут ли какие-нибудь три точки лежать на одной прямой?                                      (нет)

-        прямая l ||  плоскости a. Существует ли на плоскости a  прямая, не параллельная l  ?                                                                       (да)

-        в равнобедренной трапеции углы относятся как 4:5. Вычислить эти углы.                                                                                    (80^о; 100^о)

-        уравнение окружности x² + y² = 16. На каком расстоянии находятся точки окружности от начала координат?                                (4)

-        диагонали ромба 60 и 80. Вычислить сторону ромба.          (50)

-        могут ли пересекаться плоскости, параллельные одной и той же прямой?                                                                                   (могут)

-        точка D вне плоскости, проходящей через точки A, B, C. Может ли быть трапецией четырехугольник ABCD?                               (нет)

-        на каком расстоянии от начала координат находится точка M (6; -8)?                   (10)

-        стороны параллелограмма 4 и 6, а угол между ними 45^о. Вычислите площадь параллелограмма.                                                     ()

-        концы отрезка, не пересекающего плоскость, удалены от нее на расстояние 7 и 13 см. На каком расстоянии находится от плоскости середина отрезка?                                                                         (10)

-        сторона правильного треугольника 6. Вычислить S .               ()

Решение задач по готовым чертежам.

Задача 1.

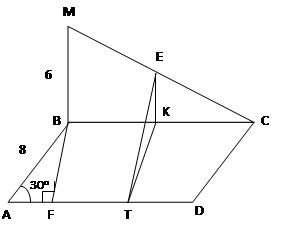ABCD – ромб со стороной a = 8 и острым углом a= 30^о. Из вершины тупого угла B восстановлен ^BM к плоскости ромба. Найдите расстояние от точки E до прямой АД, где EÎ MC, AB = 8,  ВМ=6,  МЕ:МС=1:2.

                                                 Решение.

EK = 3; BF = 4, тогда по теореме Пифагора:

ET =  = 5

Задача 2.

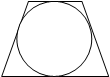
В трапецию вписана окружность. Вспомните все теоремы, которые можно применить при решении задач.

Задача 3.

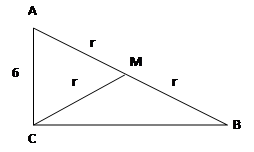
Один из катетов прямоугольного треугольника равен 6, а радиус описанной около него окружности 5. Найти площадь этого треугольника.                     Решение.

AB = 10 , ( т.к. радиус описанной окружности равен половине гипотенузы) .   Найдём СВ. СВ²  =  100 – 36 = 64 ; CB = 8, тогда площадь треугольника АВС равна 24.

 Задача 4.

BК – медиана DABC. Прямая MA перпендикулярна плоскости. Найдите угол между прямыми МА и ВК.

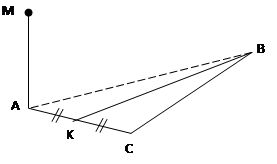Т.к. прямая МА перпендикулярна  плоскости АВС, то она перпендикулярна любой прямой, лежащей в этой плоскости.

         Задача 5.

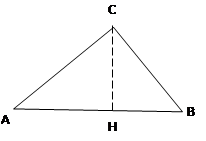Гипотенуза прямоугольного треугольника равна 10 см, проекция меньшего катета на гипотенузу равна 3,6 см. Найти  радиус  круга,  вписанного в этот треугольник.

     Þ

   24 = 12 · r

   r = 2 см

Задача 6.

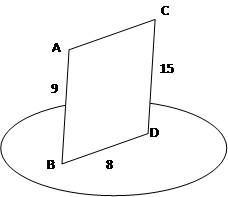Прямые AB и CD перпендикулярны  некоторой  плоскости  и пересекают её в точках B и D соответственно. Найти AC, если AB = 9;

 CD = 15; BD = 8.     

                                              Решение.

15 – 9 = 6, 

                                 Практикум по решению задач.

                               (группа делится на 3 подгруппы)

Каждой группе выдается маршрутный лист с задачами. Студенты должны оформить решение задач и защитить их решение на доске.

                        Подведение итогов урока.