Задачи по теме Системы счисления Примеры решения

Задачи по теме "Системы счисления"

                                        Примеры решения

Задание №1. 
Сколько значащих цифр в записи десятичного числа 357 в системе счисления с основанием 3? 
Решение: 
Переведём число 35710 в троичную систему счисления: 
 
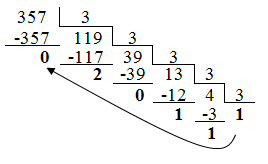
Итак, 35710 = 1110203. Число 1110203 содержит 6 значащих цифр. 
Ответ: 6.  

Задание №2. 
Дано А=A715, B=2518. Какое из чисел C, записанных в двоичной системе, отвечает условию A<c<b? 
1) 101011002 
2) 101010102 
3) 101010112 
4) 101010002 
Решение: 
Переведём числа А=A715 и B=2518 в двоичную систему счисления, заменив каждую цифру первого числа соответствующей тетрадой, а каждую цифру второго числа – соответствующей триадой: A715= 1010 01112; 2518 = 010 101 0012. 
Условию a<b<c Ответ: 101010002 (вариант 4). 

Задание №3. 
На какую цифру оканчивается запись десятичного числа 123 в системе счисления с основанием 6? 
Решение: 
Переведём число 12310 в систему счисления с основанием 6: 
 
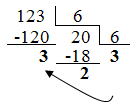
12310 = 3236. 
Ответ: Запись числа 12310 в системе счисления с основанием 6 оканчивается на цифру 3. 
Задания на выполнение арифметических действий над числами, представленными в разных системах счисления 

Задание №4. 
Вычислите сумму чисел X и Y, если X=1101112, Y=1358. Результат представьте в двоичном виде. 
1) 100100112 2) 100101002 3) 110101002 4) 101001002 
Решение: 
Переведём число Y=1358 в двоичную систему счисления, заменив каждую его цифру соответствующей триадой: 001 011 1012. Выполним сложение: 
 
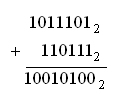
Ответ: 100101002 (вариант 2). 

Задание №5. 
Найдите среднее арифметическое чисел 2368, 6С16 и 1110102. Ответ представьте в десятичной системе счисления. 
Решение: 
Переведём числа 2368, 6С16 и 1110102 в десятичную систему счисления: 
 
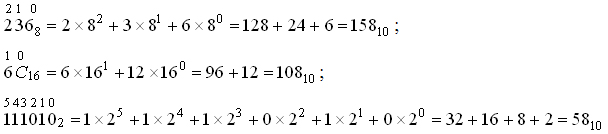
Вычислим среднее арифметическое чисел: (158+108+58)/3 = 10810. 
Ответ: среднее арифметическое чисел 2368, 6С16 и 1110102 равно 10810. 

Задание №6. 
Вычислите значение выражения 2068 + AF16 ? 110010102. Вычисления производите в восьмеричной системе счисления. Переведите ответ в десятичную систему. 
Решение: 
Переведём все числа в восьмеричную систему счисления: 
2068 = 2068; AF16 = 2578; 110010102 = 3128 
Сложим числа: 
 
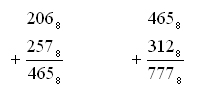
Переведём ответ в десятичную систему: 
 
Ответ:51110. 

Задания на нахождение основания системы счисления 

Задание №7. 
В саду 100q фруктовых деревьев: из них 33q яблони, 22q груши, 16q слив и 17q вишен. Найдите основание системы счисления, в которой посчитаны деревья. 
Решение: 
Всего в саду 100q деревьев: 100q = 33q+22q+16q+17q. 
Пронумеруем разряды и представим данные числа в развёрнутой форме: 
 
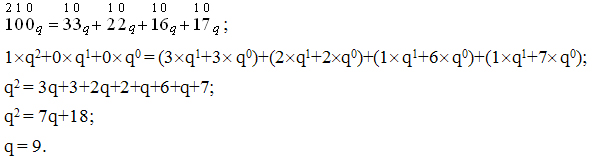
Ответ: Деревья посчитаны в системе счисления с основанием 9. 

Задание №8. 
Найдите основание x системы счисления, если известно, что 2002x = 13010. 
Решение: 
Пронумеруем разряды и запишем данные числа в развёрнутой форме: 
 
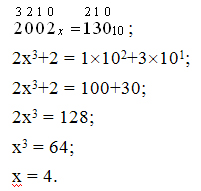
Ответ:4.

Задание №9. 
В системе счисления с некоторым основанием десятичное число 18 записывается в виде 30. Укажите это основание. 
Решение: 
Примем за х основание неизвестной системы счисления и составим следующее равенство: 
1810 = 30x; 
Пронумеруем разряды и запишем данные числа в развёрнутой форме: 
 
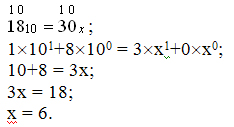
Ответ: десятичное число 18 записывается в виде 30 в системе счисления с основанием 6.