Задание 6 - 10 ОГЭ по Информатике 2025

ЗАДАНИЕ 6. ОГЭ по информатике 2023

Задача 6.1. Ниже приведена программа, записанная на пяти языках программирования.

Было проведено 9 запусков программы, при которых в качестве значений переменных s и t вводились следующие пары чисел:

(1, 2); (11, 2); (1, 12); (11, 12); (–11, –12); (–11, 12); (–12, 11); (10, 10); (10, 5).

Укажите целое значение параметра А, при котором для указанных входных данных программа напечатает «NO» четыре раза.

Решение:

(1, 2); (11, 2); (1, 12); (11, 12); (–11, –12); (–11, 12); (–12, 11); (10, 10); (10, 5).

Заметим, что программа напечатает «NO», если переменная s будет меньше или равна 10, И переменная t будет меньше или равна А.

Из первой части условия получаем, что при вводе значений s и t (11, 2) и (11, 12) программа напечатает «YES» вне зависимости от значения A.

(1, 2); (11, 2); (1, 12); (11, 12); (–11, –12); (–11, 12); (–12, 11); (10, 10); (10, 5).

Заметим, что при A = 1 программа напечатает «NO» один раз (–11, –12),

при 2 ≤ A ≤ 4 программа напечатает «NO» два раза (–11, –12)(1, 2),

при 5 ≤ A ≤ 9 программа напечатает «NO» три раза (–11, –12)(1, 2)(10, 5),

при А = 10 программа напечатает «NO» 4 раза (–11, –12)(1, 2)(10, 10) (10, 5).

Укажите целое значение параметра А: 10

Ответ: 10

Задача 6.2. Ниже приведена программа, записанная на пяти языках программирования.

Было проведено 9 запусков программы, при которых в качестве значений переменных s и t вводились следующие пары чисел:

(13, 2); (11, 12); (–12, 12); (2, –2); (–10, –10); (6, –5); (2, 8); (9, 10); (1, 13).

Укажите количество целых значений параметра А, при которых для указанных входных данных программа напечатает «NO» четыре раза.

Решение:

Заметим, что программа напечатает «NO», если переменная s будет меньше или равна A, или переменная t будет меньше или равна 12.

Из второй части условия получаем, что при вводе значений s и t (1, 13) программа напечатает «YES» вне зависимости от значения A.

(13, 2); (11, 12); (–12, 12); (2, –2); (–10, –10); (6, –5); (2, 8); (9, 10); (1, 13).

Заметим, что при -12 ≤ A ≤ 1 программа напечатает «NO» два раза (–12, 12) (–10, –10),

при 2 ≤ A ≤ 5 программа напечатает «NO» 4 раза (–12, 12) (2, –2) (–10, –10) (2, 8).

Укажите количество целых значений параметра А: 4, А = 2, А = 3, А = 4, А = 5.

Ответ: 4

Задача 6.3. Ниже приведена программа, записанная на пяти языках программирования.

Было проведено 9 запусков программы, при которых в качестве значений переменных s и t вводились следующие пары чисел:

(1, 2); (11, 2); (1, 12); (11, 12); (–11, –12); (–11, 12); (–12, 11); (10, 10); (10, 5).

Укажите наименьшее целое значение параметра А, при котором для указанных входных данных программа напечатает «YES» два раза.

Решение:

s > 10 или t > A - «YES», значит программа напечатает «YES», если переменная s будет больше 10 или переменная t будет больше А.

Получаем:

(11, 2); (11, 12)  - YES  вне зависимости от А, так как 11 > 10. У нас уже есть два раза. Дальше надо получать NO.

Для остальных вводимых данных составим массив ввода t по увеличению их значений (-12, 2, 5, 10, 11, 12, 12). То есть если A будет больше или равно максимальному в массиве, то получим во всех случаях "NO", что нам и надо. Значит А = 12

Ответ: 12

Задании взяты по ссылке: https://gdzotvet.ru/oge-ege/informatika/531-zadanie-6-oge-po-informatike-analiz-programmy

ЗАДАНИЕ 7. ОГЭ по информатике 2023

Задача 7.1. Доступ к файлу txt.com, находящемуся на сервере net.ru, осуществляется по протоколу http. Фрагменты адреса файла закодированы цифрами от 1 до 7. Запишите последовательность этих цифр, кодирующую адрес указанного файла в сети Интернет.

1) /
2) net
3) .com
4) ://
5) .ru
6) http
7) txt

Решение: протокол : // сервер / файл   

http :// net.ru / txt.com

Ответ: 6425173

Задача 7.2. Доступ к файлу htm.txt, находящемуся на сервере com.ru, осуществляется по протоколу http. Фрагменты адреса файла закодированы цифрами от 1 до 7. Запишите последовательность этих цифр, кодирующую адрес указанного файла в сети Интернет.

1) /

2) com

3) .txt

4) ://

5) .ru

6) htm

7) http

Решение: протокол : // сервер / файл   

http://com.ru/htm.txt

Ответ: 7425163

Задача 7.3. Почтовый ящик Plotnikov_11klass находится на сервере school.pochta.ru. Фрагменты адреса электронной почты закодированы буквами от А до Е. Запишите последовательность букв, кодирующую этот адрес.

А) @

Б) 11klass

В) .ru

Г) school.

Д) Plotnikov_

Е) pochta

Решение: почтовый ящик @ сервер

Plotnikov_11klass@school.pochta.ru

Ответ: ДБАГЕВ

Задача 7.4. На сервере GorodN.ru находится почтовый ящик wait_for_mail. Фрагменты адреса электронной почты закодированы буквами от А до Е. Запишите последовательность букв, кодирующую этот адрес.

А) GorodN

Б) mail

В) for_

Г) .ru

Д) wait_

Е) @

Решение: почтовый ящик @ сервер

wait_for_mail@GorodN.ru

Ответ: ДВБЕАГ

Задании взяты по ссылке:  https://gdzotvet.ru/oge-ege/informatika/538-zadanie-7-oge-po-informatike-s-otvetami-adresa-fipi

Задача 7.5.  На месте преступления были обнаружены четыре обрывка бумаги. Следствие установило, что на них записаны фрагменты одного IP-адреса. Криминалисты обозначили эти фрагменты буквами А, Б, В и Г:

Восстановите IP-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.

Решение:

ХХХ.ХХХ.ХХХ.ХХХ    ХХХ < 256      255.255.255.255

22 2.12 5.121 .30

Ответ: БАГВ

Задача 7.6.  Миша записал IP-адрес школьного сервера на листке бумаги и положил его в карман куртки. Мишина мама случайно постирала куртку вместе с запиской. После стирки Миша обнаружил в кармане четыре обрывка с фрагментами IP-адреса. Эти фрагменты обозначены буквами А, Б, В и Г:

Восстановите IP-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.

Решение:

ХХХ.ХХХ.ХХХ.ХХХ    ХХХ < 256      255.255.255.255

17 9.13 4.144 .44

Ответ: АГВБ

Задании взяты по ссылке:  https://inf-oge.sdamgia.ru/test?theme=17

ЗАДАНИЕ 8. ОГЭ по информатике 2023

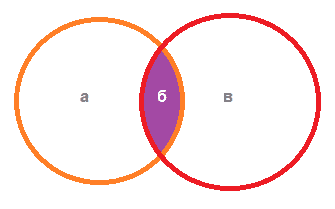
1. Формула для двух запросов А и В:

P_A = P_А|B + P_A&B – P_B

Круги Эйлера

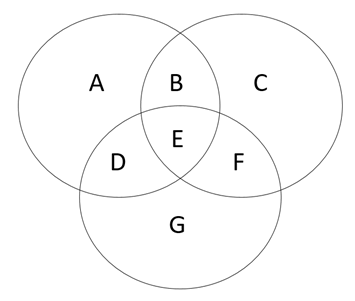
2. Формула для трех запросов А, В и С:      

P_A|B|C = P_A + P_B + P_C – P_A&B – P_A&C – P_B&C + P_A&B&C

Круги Эйлера

Задача 8.1. В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Какое количество страниц (в тысячах) будет найдено по запросу Стихи | Книга?

Считается, что все запросы выполнялись практически одновременно, так что хранящаяся на поисковом сервере информация о наборе страниц, содержащих все искомые слова, не изменялась за время выполнения запросов.

Решение:

Даны два запроса: Книга и Стихи

По формуле 1: P_A = P_А|B + P_A&B – P_B , находим запрос P_А|B (Стихи | Книга)

P_А|B = P_A + P_B – P_A&B

Стихи | Книга = 3110 + 1880 – 540 = 4450

Ответ: 4450

Задача 8.2. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Какое количество страниц (в тысячах) будет найдено по запросу Юпитер?

Решение:

Даны два запроса: Юпитер и Сатурн

По формуле 1: P_A = P_А|B + P_A&B – P_B , находим запрос P_А (Юпитер)

P_A = P_А|B + P_A&B – P_B

Юпитер = 10240 + 900 – 6000 = 5140     Ответ: 5140

Задача 8.3. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Какое количество страниц (в тысячах) будет найдено по запросу Скорпион & Козерог?

Решение:

Даны два запроса: Скорпион и Козерог

По формуле 1: P_A = P_А|B + P_A&B – P_B , находим запрос P_A&B (Скорпион & Козерог)

P_A&B = P_B + P_A – P_А|B

Скорпион & Козерог = 3300 + 1900 – 4300 = 900    Ответ: 900

Задача 8.4. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Какое количество страниц (в тысячах) будет найдено по запросу Мадрид & Париж?

Решение:

Даны три запроса: Мадрид, Берлин и Париж

Если даны три запроса, смотрим можно ли убрать какой-нибудь запрос.

В данной задаче можно убрать запрос Мадрид &, и получаем два запроса

Какое количество страниц (в тысячах) будет найдено по запросу Париж?

По формуле 1: P_A = P_А|B + P_A&B – P_B , находим запрос P_А (Париж)

P_A = P_А|B + P_A&B – P_B

Париж = 815+ 220 – 550 = 485 

 Ответ: 485

Задача 8.5. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Какое количество страниц (в сотнях тысяч) будет найдено по запросу Филателист & Марка?

Решение: Филателист & Марка (Ф&М)

Даны три запроса: Марка, Автомобиль и Филателист

Если даны три запроса, смотрим можно ли убрать какой-нибудь запрос.

В задаче нельзя убрать запросы, поэтому по формуле 2 ищем запрос:

М|А|Ф = М + А + Ф – М&А – А&Ф – Ф&М + М&А&Ф

239 = 103 + 102 + 69 – 25 – 0 – Ф&М + М&А&Ф

Подставляя значения получаем выражение, где Ф&М необходимо найти и М&А&Ф неизвестно.

Ф&М – М&А&Ф = 249 – 239

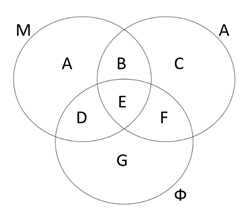 А&Ф = { E, F } = E + F = 0 => E = F = 0 

М&А&Ф = { E } => E = 0

Ф&М – М&А&Ф = 249 – 239

Ф&М – 0 = 249 – 239

Ф&М  = 10

Ответ: 10

Задании взяты по ссылке:  https://easy-exam.ru/task3168/

Задача 8.6. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Какое количество страниц (в сотнях тысяч) будет найдено по запросу Слон?

Решение: Слон (С)

Даны три запроса: Ладья, Слон и Хобот

Если даны три запроса, смотрим можно ли убрать какой-нибудь запрос.

В задаче нельзя убрать запросы, поэтому по формуле 2 ищем запрос:

Л|С|Х = Л + С + Х – Л&С – С&Х – Х&Л + Л&С&Х

66 = 25 + С + 28 – 12 – 20 – 0 + Л&С&Х

66 = 21 + С + Л&С&Х

С + Л&С&Х = 66 – 21 = 45

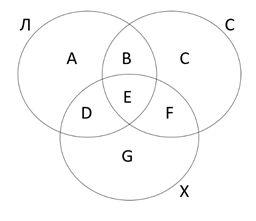 Х&Л = { D, E } = D + E = 0 => D = E = 0

Л&С&Х = { E } = E = 0

С + 0 = 45

C = 45

ОТВЕТ: 45

Задании взяты по ссылке:  https://easy-exam.ru/task3109/

ЗАДАНИЕ 9. ОГЭ по информатике 2023

Задача 9.1. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

Решение:

Задача без дополнительных условий: проходящий или не проходящих через какие-то дороги

А будет равен единице, так как А начало:

А = 1

Из города А в город Б и Г проходит только одна дорога, поэтому:

 Б = 1 и Г = 1

В город В проходят три дороги из А = 1, Б = 1, Г = 1 складываем получаем:

В = 1 + 1 + 1 = 3: В = 3

В Д проходят две дороги из Б и В, а Е проходят из В и Г складываем получаем:

Д = 1 + 3 = 4;   Е = 1 + 3 = 4

Отсюда К = В + Е + Д = 3 + 4 + 4 = 11

Ответ: 11

Задача 9.2. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З?

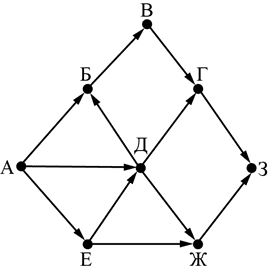 Решение: А = 1

Е = А = 1

Д = А + Е = 1 + 1 = 2

Б = А + Д = 1 + 2 = 3

В = Б = 3

Ж = Е + Д = 1 + 2 = 3

Г = В + Д = 3 + 2 = 5

З = Г + Ж = 3 + 5 = 8

Ответ: 8

Задача 9.3. На рисунке изображена схема дорог, связывающих города A, B, C, D, E, F, G. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город G?

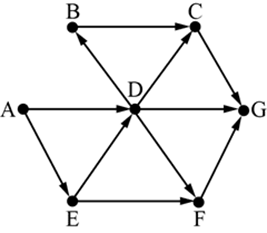 Решение: А = 1

E = A = 1

D = A + E = 1 + 1 = 2

B = D = 2

C = B + D = 2 + 2 = 4

F = E + D = 1 + 2 = 3

G = D + C + F = 2 + 4 + 3 = 9

Ответ: 9

Задании взяты по ссылке:  https://gdzotvet.ru/oge-ege/informatika/546-zadanie-9-oge-po-informatike-s-otvetami-skhema-dorog

Задача 9.4. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К, проходящих через город В?

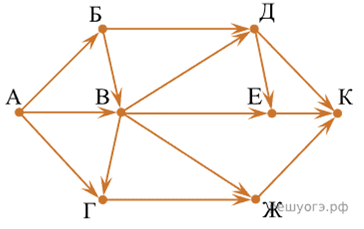
Решение:

Задача с дополнительным условием: проходящих через город В

А = 1

Б = А = 1

В = А + Б = 1 + 1 = 2

Г = В = 2 (А не учитываем, поскольку путь должен проходить через город В)

Д = В = 2 (Б не учитываем, поскольку путь должен проходить через город В)

Е = Д + В = 2 + 2 = 4

Ж = Г + В = 2 + 2 = 4

К = Д + Е + Ж = 2 + 4 + 4 = 10

Ответ: 10

Задании взяты по ссылке: https://inf-oge.sdamgia.ru/test?theme=22

Задача 9.5. На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из пункта А в пункт Л, не проходящих через пункт Е?

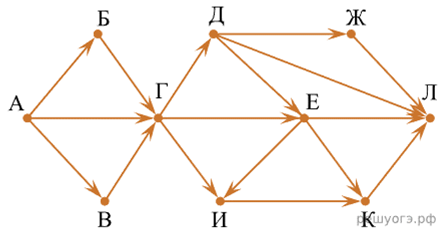
Решение:

Задача с дополнительным условием: не проходящих через пункт Е

А = 1

Б = А = 1

В = А = 1

Г = А + Б + В = 1 + 1 + 1 = 3

Д = Г = 3

И = Г = 3

(Е не учитываем, поскольку путь не должен проходить через город Е)

Ж = Д = 3

К = И = 3

(Е не учитываем, поскольку путь не должен проходить через город Е)

Л = Д + Ж + К = 3 + 3 + 3 = 9

(Е не учитываем, поскольку путь не должен проходить через город Е)

Ответ: 9.

Задании взяты по ссылке: https://inf-oge.sdamgia.ru/test?theme=22

ЗАДАНИЕ 10. ОГЭ по информатике 2023

Задача 10.1. Переведите число 110110 из двоичной системы счисления в десятичную систему счисления. В ответе напишите полученное число.

Решение:

110110₂ = 1∙2⁵ + 1∙2⁴ + 0∙2³ + 1∙2² + 1∙2¹ + 0∙2⁰ = 32 + 16 + 0 + 4 + 2 + 0 = 54₁₀

Ответ: 54

Задача 10.2. Переведите число 1101011 из двоичной системы счисления в десятичную систему счисления. В ответе напишите полученное число.

Решение:

1101011₂ = 1∙2⁶ + 1∙2⁵ + 0∙2⁴ + 1∙2³ + 0∙2² + 1∙2¹ + 1∙2⁰ = 64+32+0+8+0+2+1 = 107₁₀

Ответ: 107

Задача 10.3. Некоторое число в двоичной системе счисления записывается как 11010010. Запишите это число в десятичной системе.

Решение:

11010010₂ = 1∙2⁷+1∙2⁶+0∙2⁵+1∙2⁴+0∙2³+0∙2²+1∙2¹+0∙2⁰ = 128 + 64 + 16 +2 = 210₁₀

Ответ: 210

Задача 10.4. Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

38₁₆, 75₈, 110100₂.

Решение: Переведём все числа в десятичную систему счисления:

38₁₆ = 3∙16¹ + 8∙16⁰ = 48 + 8 = 56₁₀

75₈ = 7∙8¹ + 5∙8⁰ = 56 + 5 = 61₁₀

110100₂ = 1∙2⁵ + 1∙2⁴ + 0∙2³ + 1∙2² + 0∙2¹ + 0∙2⁰ = 32 + 16 + 4 = 52₁₀

Наибольшим среди этих трёх чисел является число 61.

Ответ: 61

Задача 10.5.  Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите минимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

20₁₆, 36₈, 11100₂.

Решение: Переведём все числа в десятичную систему счисления:

20₁₆ = 2∙16¹+0∙16⁰ = 32+0 = 32₁₀

36₈ = 3∙8¹+6∙8⁰ = 24+6 = 30₁₀

11100₂ = 1∙2⁴+1∙2³+1∙2²+0∙2¹+0∙2⁰ = 16+8+4+0+0 = 28₁₀

Наименьшим среди этих трёх чисел является число 28.

Ответ: 28

Задании взяты по ссылке:  https://gdzotvet.ru/oge-ege/informatika/523-zadanie-10-oge-po-informatike-s-otvetami-perevod-chisel-iz-desyatichnoj-sistemy-ischisleniya-fipi

Задача 10.6. Среди приведённых ниже трёх чисел, записанных в десятичной системе счисления, найдите число, сумма цифр которого в восьмеричной записи наименьшая. В ответе запишите сумму цифр в восьмеричной записи

этого числа.

55₁₀, 83₁₀, 91₁₀.

Решение: Переведём все числа в восьмеричную систему счисления:

55₁₀ = 67₈ , сумма цифр — 6 + 7 = 13;
83₁₀ = 123₈ , сумма цифр — 1 + 2 + 3 = 6;
91₁₀ = 133₈ , сумма цифр — 1 + 3 + 3 = 7.

Наименьшей суммой цифр в восьмеричной записи числа является число 6.

Ответ: 6

Задача 10.7. Среди приведённых ниже трёх чисел, записанных в десятичной системе счисления, найдите число, в двоичной записи которого наименьшее количество единиц. В ответе запишите количество единиц в двоичной записи этого числа.

59₁₀, 71₁₀, 81₁₀.

Решение: Переведём все числа в двоичную систему счисления:

 59₁₀ = 111011₂ , количество единиц  — 5;
 71₁₀ = 1000111₂ , количество единиц  — 4;
 81₁₀ = 1010001₂ , количество единиц  — 3.

Наименьшим количеством единиц в двоичной записи числа является 3. Ответ: 3

Задании взяты по ссылке:  https://gdzotvet.ru/oge-ege/informatika/523-zadanie-10-oge-po-informatike-s-otvetami-perevod-chisel-iz-desyatichnoj-sistemy-ischisleniya-fipi

Задача 10.8. Переведите число 87 из десятичной системы счисления в двоичную систему счисления. В ответе укажите двоичное число. Основание системы счисления указывать не нужно.

Решение:

Задача 10.9. Переведите число 101 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число – количество единиц.

Решение:

Задача 10.10. Переведите число 143 из десятичной системы счисления в двоичную систему счисления. Сколько значащих нулей содержит полученное число? В ответе укажите одно число – количество нулей.

Решение:

Задании взяты по ссылке:  https://gdzotvet.ru/oge-ege/informatika/523-zadanie-10-oge-po-informatike-s-otvetami-perevod-chisel-iz-desyatichnoj-sistemy-ischisleniya-fipi

Скачано с www.znanio.ru