Публикация является частью публикации:

Заняття – конференція на тему "Застосування похідної до розв'язання прикладних задач"

Міністерство освіти і науки України

ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД

«КРАСНОДОНСЬКИЙ ПРОМИСЛОВО – ЕКОНОМІЧНИЙ КОЛЕДЖ»

…кожда математична теорема здійснюється де-небудь у природі,

в какій-небудь комбінації молекул або елементів.

Математика здається нам відверненої тільки тому,

що ми не помічаємо використання її принципів у природі.
П.Чаадаєв

ЗАСТОСУВАННЯ ПОХІДНОЇ ДО

РОЗВ’ЯЗУВАННЯ ПРИКЛАДНИХ ЗАДАЧ

заняття – конференція

(засідання «наукової ради»)

І курс

Підготувала

Салюк О.М.

викладач математики

вищої категорії

Краснодон 2014

МЕТА:

- показати широке застосування похідної; довести, що похідна – засіб дослідження процесів дійсності і сучасного виробництва;

- перевірити знання студентами формул для знаходження похідної та вміння застосовувати метод диференціального числення до розв’язування прикладних задач, вміння виділяти етапи в розв’язуванні прикладних задач;

- встановлювати міжпредметні зв’язки математики з фізикою, електротехнікою та економікою, підвищуючи цим ефективність технічної, практичної спрямованості навчання;

- розвивати уміння узагальнювати цілісну систему знань, уміння реалізувати практичні зв’язки курсу математики з майбутньою професією, уміння через організацію ділової рольової гри відображувати виробничу ситуацію та розвивати творче і логічне мислення, усне та писемне мовлення; набуття студентами публічних виступів і дискутувань, відстоювання своєї позиції;

- виховувати у студентів бажання мати глибокі й міцні знання, працьовитість та уважність; розвивати інтерес до математики.

ОБЛАДНАННЯ:

комп’ютер, мультимедійний пристрій, дидактичний матеріал, тести.

ПРИМІТКА:

студенти готуються до заняття заздалегідь: підбирають задачі, готують презентації з даної теми, шукають історичний матеріал. Перед заняттям серед студентів групи визначаються: прес - центр три студента, секретар Наукової ради та лаборант.

ЕПІГРАФ УРОКУ:

“Музика може піднімати або умиротворяти душу,
Живопис – радувати око,
Поезія – будити почуття,
Філософія – задовольняти потреби розуму,
Інженерна справа – удосконалювати матеріальну сторону життя людей,
А математика здатна досягтися всіх цих цілей”.

Так сказав американський математик Моріс Клайн.

ХІД ЗАНЯТТЯ

1 етап заняття: Організаційний момент

Дайте молодим те, в чому вони відчувають потребу, щоб вони мали можливість робити свій вибір незалежно від нас.

(К. Поппер)

Привітання: Добрий день шановні, вітаю всіх присутніх! Перевірка присутніх, призначення чергових.

2 етап заняття: Мотивація навчальної діяльності.

Те, про що ми будемо говорити на сьогоднішньому занятті, уже відкрито. Але, можливо, щось нове ви відкриєте сьогодні для себе.

На попередніх заняттях ви засвоїли одне із фундаментальних понять алгебри і початків аналізу – похідна. За допомогою похідної ми досліджували і будували графіки функції, знаходили найбільше і найменше значення функції на відрізку, складали рівняння дотичної. І, мабуть, у вас виникало питання: «А навіщо?».

І наше підсумкове заняття з цієї теми повинне бути відповіддю на це запитання.

Готуючись до заняття, ви отримали проблемні завдання, щоб відповісти на запитання «А навіщо?».

3 етап заняття: Актуалізація, вступне слово вчителя. (Оголошується тема і мета заняття.) Тема нашого заняття «Застосування похідної до розв’язання прикладних задач»

МЕТА нашого заняття:

- переконатися, що похідна – засіб дослідження процесів дійсності і сучасного виробництва;

- закріпити знання формул для знаходження похідної та правил диференціювання;

- показати що знання з математики тісно повязанні зі знаннями фізики, електротехніки та економіки;

1. Згадайте будь ласка, визначення похідної.

2. За якими двома етапами знаходиться похідна.

3. Сформулюйте правило диференціювання для додатку.

4. Чому дорівнює за таблицею похідна від синуса, косинуса.

Добре.

Сьогодні у нас незвичайне заняття. Науково технічний прогрес так швидко крокує в 21 сторіччі, що навіть у нашому коледжі ми зможемо здійснити подорож у часі. І так 2020 рік сучасне місто Краснодон. Позаду ДПА, навчання у вищих навчальних закладах, як швидко минає час, і ви вже молоді наукові співробітники.

У нас сьогодні відкрите засідання наукової ради. Ми розглянемо як можна застосовувати знаходження найбільшого і найменшого значення функції в різних галузях науки.

На цьому засіданні присутні представники кафедр: історії, фізики, економіки та електротехнічних дисциплін; представники преси, спостерігачі та фахові консультанти. Для роботи конференції необхідно вибрати секретаря, які будуть пропозиції. Добре секретарем конференції обрано – Артеменко Ольгу.

4 етап заняття: Проведення конференції.

Секретар: Розпочинаємо роботу наукової ради. Мер міста Краснодон звернувся до нашого вищого навчального закладу з проблемою постачання місту електроенергії. Для аналізу та обґрунтування данного питання слово надається представнику кафедри історії Склярову Івану.

( Слайд кафедри «Історії»)

Вперше поняття похідної зустрічалося в роботах італійського математика Ніколо Тарталі ( близько 1500 – 1557 рр.) – він розглядав задачу про кут нахилу знаряддя, при якому забезпечується найбільша дальність польоту снаряда.

Похідна — основне поняття диференціального числення, що характеризує швидкість зміни функції.

Визначається як межа відносини приросту функції до приросту її аргументу при прагненні приросту аргументу до нуля, якщо така межа існує.

Таким чином,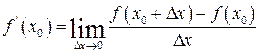

Але найважливіші наукові досягнення були зроблені Лейбниц і Ньютон, незалежно один від одного, вони створили математичний аналіз — диференціальне й інтегральне числення засновані на нескінченно малих величинах.

Диференціальне числення було відкрите наприкінці 17 сторіччя на основі двох задач:

· про дослідження дотичної до довільної лінії;

· про дослідження швидкості при довільному законі руху.

Ньютон зробив своє відкриття 1665—1666 роки.

Будучи ще студентом, Ньютон зрозумів, що диференціювання й інтегрування — взаємне зворотні операції. Ця основна теорема аналізу вже більш-менш ясно вимальовувалася в роботах Торричеллі, Грегорі та Барроу, однак лише Ньютон зрозумів, що на цій основі можна одержати не тільки окремі відкриття, але потужне системне числення, подібне алгебрі, із чіткими правилами й гігантськими можливостями.

У 1675: Лейбніц створив диференціальне й інтегральне числення й згодом видав головні результати свого відкриття, випередивши Ньютона, який ще раніше Лейбніца прийшов до подібних результатів, але в той час ще не публікував їх, хоча Лейбніцу деякі з них були відомі в приватному порядку.

У роботі Лейбніца викладаються основи диференціального числення, правила диференціювання виразів. Використовуючи геометричне тлумачення відносини dy/dx, він коротко роз'ясняє ознаки зростання й спадання, максимума і мінімума, випуклості та угнутості (отже, і достатні умови екстремума для найпростішого випадку), а також точки перегибу.

В 1708 році спалахнула сумно відома суперечка Лейбніца з Ньютоном про науковий пріоритет відкриття диференціального числення. Відомо, що Лейбніц і Ньютон працювали над диференціальним численням паралельно й що в Лондоні Лейбніц ознайомився з деякими неопублікованими роботами й листами Ньютона, але прийшов до таких же результатів самостійно.

В 1693 році, коли Ньютон, нарешті, опублікував перший короткий виклад своєї версії аналізу, він обмінявся з Лейбніцем дружніми листами.

Але задача на використання похідної виникали ще раніше:

Уже в далекій давнині виникали ситуації, коли було потрібно вирішувати задачі на екстремум. Одна з перших, що дійшли до нас, задач подібного роду пов'язана з легендою про заснування міста Карфагена. Як оповідає в «Енеїді» римський поет Вергілій, давним-давно фінікійська царівна Дідона з невеликим загоном відданих їй людей покинула рідне місто Тир, рятуючись від переслідувань свого брата тирана Пігмаліона. Її кораблі відправилися на захід по Середземному морю й плили, поки Дідона не облюбувала зручне для поселення місце на африканськім узбережжі, у нинішній Туніській затоці.

Фінікійці, які щойно висадилися були зустрінуті не дуже гостинно місцевими жителями, нумідійцями. Король нубідійців Ярб войовничо й презирливо розмовляв з непрошеною гостею. Він прийняв коштовності, запропоновані Дідоной для покупки землі, але рішуче заявив, що замість він згодний поступитися їй лише клаптик землі, «який можна оточити бичачою шкірою». Царівна безмовно погодилася. Ярб зрозумів хитрість і підступництво фінікіянки занадто пізно: Дідона наказала розрізати шкіру на дуже тонкі ремені й зшити їх. Одержавши, таким чином, тонкий, але дуже довгий ремінь, вона відгородила ним від берега значну територію. Простодушний, але чесний Ярб не став відмовлятися від даного слова. А Дідона на цьому місці заснувала місто Карфаген. На згадку про цю історію карфагенська міцність була названа «Бірса», що мовою мешканців Карфагена означає «бичача шкіра».

Легенда відносить події до 825 року до н.е. і нам, звичайно, судити про їхню вірогідність важко. Але для нас цікава математична задача, яку, очевидно, довелося вирішувати Дідоне. Припустимо, що довжина виготовленого тонкого ременя рівна 600м. Тоді сучасною мовою задача Дідони формулюється так:

Задача. Одна сторона прямокутної ділянки землі примикає до берега моря, а три інші огороджуються ременем, довжина якого 600м. Які повинні бути сторони цієї ділянки, щоб його площа була найбільшою?

Розв’язок. Нехай одна сторона прямокутника рівна х м, тоді інша сторона рівна

(600 – 2х)м. Площа прямокутника буде функцією від змінної х:

у = х(600 – 2х) = 600х – 2х², область визначення якої (0; 300).

Знайдемо найбільше значення цієї функції на інтервалі (0; 300).
Похідна цієї функції у' = 600 – 4х.
Критичну точку знайдемо з рівняння 600 – 4х = 0

х = 150.

Досліджуємо знак похідної на кожному інтервалі:

(0; 150) у' > 0
(150; 300) у' < 0

Так як при переході через точку х = 150 похідна змінює знак з плюса на мінус, тоді при х = 150 функція має максимум. Отже, найбільшу площу прямокутник буде мати зі сторонами 150 м і 300 м.
Знайдемо площу ділянки землі, яка була огороджена S = 45000 м².

Ми розв'язали задачу Дідони, вважаючи, що ділянка має форму прямокутника. Розв'язок подібних задач, якщо форма границі – крива лінія викликало до життя новий важливий розділ математики – варіаційне обчислення.

На прикладі цієї задачи ми побачили, як у повсякденному житті, у практичних задачах часто виникає необхідність визначення умов, при яких ми одержуємо найкращі результати.

Питання преси: Читачі журналу «Знання-сила» цікавляться, звідки пішло диференціальне числення, де його джерела та хто намагався розв’язати перші задачі?

Секретар: Дякуємо представнику кафедри історії. Звісно, не змогли залишитися байдужими молоді фізики, слово надається Ретівовій Світлані

( Слайд кафедри «Фізики»)

Далі виходить фізик:

При вивченні тих або інших процесів і явищ часто виникає задача визначення швидкості цих процесів. Її розв'язок приводить до поняття похідної, що є основним поняттям диференціального числення.

В фізиці похідна застосовується для знаходження закономірності зміни з часом різних характеристик електричних процесів. Наприклад, сила змінного струму є похідною від функції залежності електричного заряду, який проходить по провіднику, протягом часу. Або ЕРС самоіндукції, яка виникає в провіднику індуктивностю при протіканні змінного струму, визначається так само за допомогою похідної.

Також за допомогою похідної можна вирішувати фізичні задачі на знаходження найбільших або найменших значень змінних фізичних величин.

Зупинимося на питанні: застосування похідної при вивченні теми «Електричний струм»

Перш ніж ми розглянемо застосування похідної у фізиці на прикладах, згадаємо в чому полягає фізичний сенс похідної:

1. швидкість – це перша похідна від функції руху. Яка залежить від часу : ;

2. сила струму – це перша похідна від функції заряду, яка залежить від часу:

3. потужність – це перша похідна від функції роботи, яка залежить від часу:

4. ЕРС самоіндукції – це перша похідна від функції сили струму, яка залежить від часу: .

Тепер розглянемо приклади.

Приклад 1

На конденсаторі ємністю C = 10^-6(Ф), включеного в побутову електромережу, напруга змінюється за законом U(t) = . Знайти силу струму, яка проходить через конденсатор в момент часу t = 0,01 с.

Розв’язок: З фізичного сенсу похідної нам відомо, що сила струму є похідна від функції залежності заряду на конденсаторі від часу.

Заряд на конденсаторі знаходиться за формулою: ,

де С – це ємність конденсатору, U(t)- змінна напруга на обкладках конденсатору.

Тоді функція залежності заряду від часу:

а функція залежності сила струму від часу:

Значення сили струму при t = 0,01 с:

Знак - вказує на напрямок протікання струму по провіднику.

Приклад 2

Сила струму, який проходить через котушку з індуктивністю L = 0,001Гн (Генрі), змінюється за законом =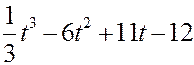. Знайдіть ЕРС самоіндукції, що виникає в котушці в момент часу t = 5 с. Знайти момент часу, коли ЕРС самоіндукції приймає найбільше значення й знайти це значення ЕРС самоіндукції.

Розв'язок.

ЕРС самоіндукції визначається за формулою .

Тоді похідна від сили струму:

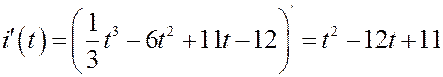Відповідно функція змінення ЕРС самоіндукції з плином часу:

При t = 5 с значення ЕРС дорівнює:

Тепер знайдемо момент часу, коли ЕРС самоіндукції приймає найбільше значення. Для цього ми знайдемо похідну , дорівняємо її до нуля та знайдемо стаціонарну точку:

с.

Досліджуємо знак похідної на кожному інтервалі, при цьому необхідно пам’ятати, що розв’язуючи задачу з фізики ми повинні враховувати область допустимих значень для часу .Відповідно до цього зауваження розглядаємо інтервали ( 0; 6) і (6; +):

( 0; 6) у' > 0
(6; +) у' < 0

Так як при переході через точку похідна змінює знак з плюса на мінус, тоді при функція має максимум. Визначимо максимальне значення ЕРС самоіндукції:

Як ми бачимо, похідна використовується не тільки в математиці, але і в фізиці. Вона необхідна для знаходження екстремального значення процесу, який відбувається при тому чи іншому фізичному явищі.

Секретар: Дякуємо представнику кафедри фізики та надаємо слово представникові кафедри електротехнічних дисциплін Ушакову Сергію.

( Слайд кафедри «Електропостачання»)

Математичні методи глибоко проникли в усі галузі людських знань у тому числі в електротехніці, електроенергетиці, електронній промисловості.

Метою моєї доповіді є розгляд прикладів використання методів

диференційного числення в електротехніці.

Для цього розглянемо розв'язок прикладної задачі при вивченні теми «Похідна і її застосування в електротехніці»

Застосуємо математичні знання, щоб допомогти студенту нашого коледжу, Казюрі Володимиру Миколаївичу, який закінчив наш навчальний заклад, і пішов працювати провідним інженером до Луганського обласного енергетичного обєднання і перед ним начальником поставлена задача:

“Шановний Володимир Миколаївич, я начальник міської вітроелектростанції, Шанюк Олександр Іванович, прошу вас виконати відповідальне завдання.

У нас на міській вітроелектростанції є генератор струму з відомою ЕРС 6 МВ та внутрішнім опором 2 Ом. До цього джерела приєднана місцева електромережа:

1) Виразіть потужність зовнішнього кола, як функцію зовнішнього опору мережі;

2) Дослідіть, при якому значенні зовнішньому опору кола потужність буде найбільшою

3) Обчисліть чому буде дорівнювати найбільша потужність.

Володимир Миколаєвич звернувся за допомогою до нашого навчального закладу і ми погодилися йому допомогти. Отримавши завдання, ми розглянули і обговорили його на засіданні циклової комісії електротехнічних дисциплін і пропонуємо наступний розв’язок.

Розв’язання

Потужність в зовнішньому колі дорівнює . За законом Ома для повного кола сила струму дорівнює , тоді отримуємо функцію залежності потужності від зовнішнього опору 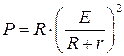або

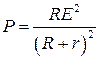(1) – потужність зовнішнього кола, як функції зовнішнього опору.

При заданих значеннях ЕРС 6 МВ та внутрішнього опору 2 Ом генератора маємо функцію 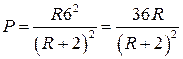(2). Визначимо максимум цієї функції. Для цього знайдемо похідну потужності від опору R і прирівняємо її нулю:

′=0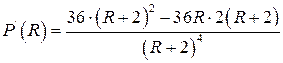

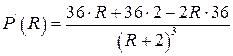
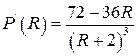
Звідси знайдемо максимальне значення потужності. Знайдемо стаціонарну точку, для чого дорівняємо до нуля похідну потужності.

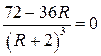
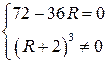
(3) – стаціонарна точка, виконаємо дослідження на екстремум.

Отже точка є точкою максимума.

При цьому , отже

Підставимо (3) в (2) і обчислимо максимальну потужність:

1) 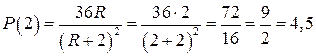Вт

Висновок

Таким чином, методом математичного аналізу ми довели, що генератор струму буде давати максимальну корисну потужність за умови узгодження опору генератора r з опором навантаження R, а саме:

При цьому максимальна потужність має значення:

Секретар: Виявили бажання й економічні світила нагадати про взаємозв’язок теоретичних пошуків з реальним життям. З доповіддю виступить провідний економість Ленов Владлен. ( Слайд кафедри «Економіки»)

Дуже важливою виробничою задачею є вміння визначити при якому обсязі виробництва питомі витрати будуть мінімальними й до яких меж можна розширювати виробництво.

Ці задачі вирішуються тільки за допомогою математики, а саме за допомогою похідної.

В економічній теорії активно використовується поняття «маржинальний», що означає «граничний». Граничні або прикордонні величини які характеризують процес, зміни економічного об'єкта. Отже, похідна виступає як інтенсивність зміни деякого економічного об'єкта (процесу) за часом або щодо іншого досліджуваного фактору.

Використання похідної для розв'язку задач по економічній теорії

Задача 1

Районне енергоуправління може передати споживачам Х Мвт*ч. електроенергії протягом дня. За договором він повинен щодня постачати КраПЕКу не менш 0,02 Мвт*ч. Виробничі потужності районного енергоуправління такі, що кількість електроенергії, яка передається споживачам не може перевищувати 50 Мвт*ч. протягом дня.

Визначити, при якій кількості відпущеної електроенергії питомі витрати районного енергоуправління будуть найбільшими (найменшими), якщо функція витрат має вигляд:

К=-х³+98х²+200х.

Питомі витрати будуть складати У=К/х=-х²+98х+200

Наша задача зводиться до відшукання найбільшого й найменшого значення функції У= -х²+98х+200. На інтервалі [0,02; 50].

Знаходимо похідну .

Прирівняємо знайдену похідну до нуля, щоб визначити стаціонарну точку.

Висновок: x=49, стаціонарна точка функції. Обчислюємо значення функції на кінцях проміжках і в стаціонарній точці.

;

Таким чином, при передачі 49 Мвт*г електроенергії в день питомі витрати будуть максимальні, а при поставці 0,02 Мвт*ч електроенергії в день мінімальні.

Задача 2

Вітрова електростанція виробляє Х кВт*год електроенергії на місяць. Встановлено, що залежність фінансових прибутків підприємства від кількості виробленої електроенергії виражається формулою f(x)=-0,02x³+600x -1000. Визначити при якій кількості електроенергії, яку виробить підприємство, буде досягатися максимальний прибуток.

Функція досліджується за допомогою похідної.

Розв'язок:

f '(x)=-0,06x²+600.

Дорівнюємо знайдену похідну до нуля, знаходимо таким чином стаціонарну точку.

f '(x)=0; - 0,06x²+600=0.

Х=100.

Визначаємо знак похідної ліворуч і праворуч від стаціонарної точки:

На інтервалі , а на інтервалі .

Одержуємо, що при Х=100 функція досягає максимуму.

f(x)=-0,02(100)³+600·100 -1000 = 39000 кВт*год

Секретар: Усі представники кафедр були заслухані. Засідання нашої наукової ради закінчено. Пропоную проект рішення:

- переконалися, що похідна – засіб дослідження процесів дійсності і сучасного виробництва;

- закріпили знання формул для знаходження похідної та правил диференціювання;

- показали що знання з математики тісно повязанні зі знаннями фізики, електротехніки та економіки;

5 етап заняття: Систематизація та узагальнення навчального матеріалу. Самостійна робота.

Дякую секретарю наукової ради за плідну співпрацю, а зараз повертаємося у сучасність і вам буде запропоновані практичні завдання прикладного характеру.

Наступні студенти:

1. Діжечко Дмитро

2. Ретівова Світлана

3. Твердохліб Олександр

4. Довбня Миколай

5. Арсєнєв Серафим

6. Слоньов Владислав

7. Іванов Дмитро

будь ласка займіть місця за комп’ютерами, всім іншим чергові будь ласка роздайте картки з індивідуальними завданнями.

ВАРІАНТ №1

1. Знайти , якщо y=(3x-1)(+4).

2. Координата матеріальної точки змінюється протягом часу за законом х(t) = 3t ² - 7t + 6. Знайдіть швидкість точки в момент часу t = 6.

ВАРІАНТ №2

1. Знайти , якщо .

2. Якщо тіло рухається по прямій його швидкість V (м/с) змінюється за законом 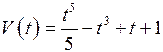, де t – час руху в секундах. Знайдіть прискорення (м/с²) через 2 секунди після початку руху.

ВАРІАНТ №3

1. Знайти , якщо .

2. На конденсаторі ємністю C = 2·10^-6(Ф), включеного в побутову електромережу, напруга змінюється за законом U(t) = . Знайти силу струму, яка проходить через конденсатор в момент часу

t = 0,005с.

ВАРІАНТ №4

1. Знайти , якщо .

2. На конденсаторі ємністю C = 4·10^-6(Ф), включеного в промислову електромережу, напруга змінюється за законом U(t) = . Знайти силу струму, яка проходить через конденсатор в момент часу

t = 0,0025 с.

ВАРІАНТ №5

1. Знайти , якщо .

2. В які моменти часу сила струму у ланцюзі дорівнює нулю, якщо кількість електрики, яка проходить крізь провідник, задається формулою .

ВАРІАНТ № 6

1. Знайти , якщо

2. На конденсаторі ємністю C = 5·10^-6(Ф), включеного в побутову електромережу, напруга змінюється за законом U(t) = . Знайти силу струму, яка проходить через конденсатор в момент часу

t = 0,02 с.

ВАРІАНТ № 7

1. Знайти , якщо

ВАРІАНТ № 8

1. Знайти , якщо

2. На конденсаторі ємністю C = 3·10^-6(Ф), включеного в промислову електромережу, напруга змінюється за законом U(t) = . Знайти силу струму, яка проходить через конденсатор в момент часу с.

ВАРІАНТ № 9

1. Знайти , якщо .

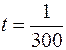2. Котушку з індуктивністю L = 0,003Гн (Генрі), включили в побутову електромережу, де сила струму змінюється за законом =. Знайдіть ЕРС самоіндукції, що виникає в котушці в момент часу с.

ВАРІАНТ № 10

1. Знайти , якщо

2. Котушку з індуктивністю L = 0,04Гн (Генрі), включили в промислову електромережу, де сила струму змінюється за законом =. Знайдіть ЕРС самоіндукції, що виникає в котушці в момент часу с.

Самостійна робота завершена. Чергові будь ласка роздайте дидактичний матеріал для самоперевірки студентам з картками, і запишіть результати роботи студентів за комп’ютером. Передайте мені заповненні бланки відомостей.

Підсумок заняття

Сьогодня ми уявляли себе майбутніми учасниками наукової конференції, але цілком реально стати учасником справжньої науково – практичної конференції, з питань застосування математики в своїй професії, але ви маєте можливість під час навчання в коледжі стати учасниками обласної науково – рактичної конференції, яка щороку проходить в місті Луганськ. Своїми враженнями від участі в такій конференції поділяться студенти четвертого курсу Каштанов Владислав та Воронін Сергій.

Я Каштанов Владислав студент гр.ОКСМ – 10 брав участь в обласній науково – практичній конференції з теми «Використання математичних знань та навичок при вивченні дисципліни «Теорія електричних і магнітних кіл». При вивченні зазначеної дисципліни ми використовували знання з вищої математики з теми «Векторна алгебра». При вивченні теорії електричних і магнітних кіл, виникає необхідність розв’язувати системи алгебраїчних рівнянь з трьома і більше невідомими, цей розв’язок доцільно виконувати матричними методами розв’язання систем алгебраїчних рівнянь. Робота викликала інтерес слухачів і її тези були надруковані в збірнику матеріалів ІІ обласної студентської науково – практичної конференції.

Я Воронін Сергій студент гр.ОКСМ – 10 разом зі студентом гр.ОКСМ -09 Комісаровим Михайлом брав участь в обласній науково – практичній конференції з теми «Математика і розробка комп’ютерних ігор». В своїй роботі ми доводили неможливість розробки комп’ютерних ігор без глибоких знань сучасних розділів математики таких як векторна алгебра, дискретна математика та аналітична геометрія. Робота отримала ІІ місце, була нагороджена грамотою та ціним призом і її тези були надруковані в збірнику матеріалів ІІІ обласної студентської науково – практичної конференції.

Оголошуються результати проведеної самостійної роботи.

Результати роботи відразу будуть оцінені: студенти які працювали з комп’ютерними тестами оголосіть свої результати черговому, студенти які працювали з індивідуальними завданнями отримують рішення свого завдання від чергового і проводять самоаналіз виконаної роботи. Всі результати чергові передають викладачеві, який оголошує отримані оцінки. Представники кафедр крім того отримують оцінку за свій виступ на науковій раді, крім того раніше була оцінена також проведена студентами попередня підготовка до конференції.

Жодна наука так не укріпляє віру в сили людского розуму, як математика.
Г.Штейнгауз

Заняття завершено. Бажаю всім успіху. Спасибі за заняття!

ДОДАТОК 1

КАРТКИ З ІНДИВІДУАЛЬНИМИ ЗАВДАННЯМИ

ВАРІАНТ №4

1. Знайти , якщо .

t = 0,0025 с.

ВАРІАНТ №1

1. Знайти , якщо y=(3x-1)(+4).

ВАРІАНТ №2

1. Знайти , якщо .

ВАРІАНТ №3

1. Знайти , якщо .

t = 0,005с.

ВАРІАНТ №5

1. Знайти , якщо .

ВАРІАНТ № 6

1. Знайти , якщо

ВАРІАНТ № 7

1. Знайти , якщо

ВАРІАНТ № 8

1. Знайти , якщо

ВАРІАНТ № 9

1. Знайти , якщо .

ВАРІАНТ № 10

1. Знайти , якщо

Використана література:

1. Нелін Є.П., Долгова О.Є.Алгебра 11 кл.. Харків. Гімназія.2011

2. Мерзляк А.Г. Алгебра і початки аналізу 11 клас. Харків.Гімназія.2010

3. Виленкин И.Я., Мордкович А.Г. Производная и интеграл. М. Просвещение. 1976

4. Беляева Е.С. Монахов В.М. Экстремальные задачи.

5. Рижов Ю.М. Похідна та її застосування. К. Вища школа. 1977

6. Парно И.К. Производная и её применение к исследованию функций. Москва. Просвещение 1968

7. Гальперіна А.Р. Алгебра і початки аналізу 11кл. Збірник завдань для контролю знань.Х. Ранок.2012.

Скачано с www.znanio.ru