
Публикация является частью публикации:
MATEMATIKA 
ALGEBRA VA ANALIZ ASOSLARI
GEOMETRIYA
I QISM
Umumiy o‘rta ta’lim maktablarining 11-sinflari va o‘rta maxsus, kasb-hunar ta’limi muassasalari uchun darslik
O‘zbekiston Respublikasi Xalq ta’limi vazirligi tomonidan tasdiqlangan
1-nashri
TOSHKENT
2018
UO‘K: 51(075.32)
KBK: 22.1ya72
M 54
Algebra va analiz asoslari bo‘limining mualliflari:
M.A. Mirzaahmedov, Sh.N. Ismailov, A.Q. Amanov Geometriya bo‘limining muallifi:
B.Q. Xaydarov
Taqrizchilar:
R.B. Beshimov – Mirzo Ulug‘bek nomidagi O‘zbekiston Milliy Universiteti “Geometriya va topologiya” kafedrasi mudiri, fizika-matematika fanlari doktori;
Q.S. Jumaniyozov – Nizomiy nomidagi TDPU Fizika-
matematika fakulteti “Matematika o‘qitish metodikasi” kafedrasi dotsenti, pedagogika fanlari nomzodi;
R.O. Rozimov – Sergeli tumani 237- umumta’lim maktabi matematika fani o‘qituvchisi;
S.B. Jumaniyozova – RTM metodisti;
S.R. Sumberdiyeva – Sergeli tumani 6- ixtisoslashtirilgan maktabi matematika fani o‘qituvchisi.
Darslikning “Algebra va analiz asoslari” bo‘limida ishlatilgan belgilar va ularning talqini:
r – masalani yechish (isbotlash) ▲ – masalani yechish boshlandi (isbotlash) tugadi
–
![]()
![]() nazorat ishlari va test (sinov) ? – savol va topshiriqlar mashqlari
nazorat ishlari va test (sinov) ? – savol va topshiriqlar mashqlari
– asosiy ma’lumot * – murakkabroq mashqlar
ISBN: 978-9943-5127-3-3 © Barcha huquqlar himoyalangan
Algebra va analiz asoslari
I BOB. HOSILA VA UNING TATBIQLARI
O‘ZGARUVCHI MIQDORLAR ORTTIRMALARINING NISBATI
 1–2 VA UNING MA’NOSI.
1–2 VA UNING MA’NOSI.
URINMA TA’RIFI. FUNKSIYA ORTTIRMASI
O‘zgaruvchi miqdorlar orttirmalarining nisbati
Turli o‘lchov birliklariga ega bo‘lgan ikkita o‘zgaruvchi miqdor nisbatini hisoblash inson hayotida tez-tez uchrab turadi.
Masalan, avtomashinaning tezligi uning yurgan yo‘lining vaqtga nisbati km/soat yoki m/s larda o‘lchanadi, yoqilg‘i sarflashi esa km/litr yoki 100 km/litr larda o‘lchanadi.
Xuddi shunday, basketbolchining mahorati bir o‘yinda to‘plagan ochkolar soni bilan belgilanadi.
Misol. O‘quv ishlab chiqarish majmuasida 11-sinf o‘quvchilari orasida matn terishning sifati va tezligi bo‘yicha sinov o‘tkazilmoqda.
Karim 3 minut mobaynida 213 ta so‘zni terib, 6 ta imloviy xatoga, Nargiza esa 4 minut mobaynida 260 ta so‘zni terib, 7 ta imloviy xatoga yo‘l qo‘ygani ma’lum bo‘ldi. Ularning natijalarini solishtiring.
r Har bir o‘quvchi uchun tegishli nisbatlarni tuzamiz:
Karim:
213ta so‘z so‘z
; matn terishning tezligi ![]() =
71
=
71
3min min
matn terishning sifati ![]() 6
ta xato ≈
0,0282
6
ta xato ≈
0,0282
![]() xato .
xato .
213 ta so‘z so‘z
Nargiza:
260ta so‘z so‘z
matn terishning tezligi ![]() = 65 ;
= 65 ;
4min min
matn terishning sifati ![]() 7
ta xato ≈
0,0269
7
ta xato ≈
0,0269
![]() xato .
xato .
260 ta so‘z so‘z
Demak, Karim matnni Nargizaga nisbatan tezroq tergan bo‘lsa-da, Nargiza bu ishni sifatliroq bajargan. ▲
1. Puls chastotasini tekshirish uchun barmoqlar uchi arteriya tomiri o‘tadigan joyga qo‘yiladi va zarbalarni his qilish uchun shu joy bosiladi. Madina pulsni o‘lchaganda bir minutda 67 ta zarbani his qildi.
a) Puls chastotasining ma’nosini tushuntiring. U qanday kattalik (belgi)?
b) Har soatda Madinaning yuragi necha marta uradi?
2. Karim uyida 14 bet matn terib, 8 ta imloviy xatoga yo‘l qo‘ydi. Agar 1 betda o‘rtacha 380 ta so‘z bo‘lsa:
a) Karimning matn terish sifatini aniqlang va yuqoridagi misolda olin-
яgan natija bilan solishtiring. Karimning matn terish sifati yaxshilandimi?
b) Karim 100 ta so‘z terganda o‘rtacha qancha xato qiladi?
3. Ma’ruf 12 soat ishlab 148 m 20 cm, Murod esa 13 soat ishlab 157 m 95 cm ariq tozaladi. Ularning mehnat unumdorligini solishtiring.
4. Avtomashina yangi shina protektorining chuqurligi 8 mm ni tashkil qiladi. 32178 km yurilganidan so‘ng yemirilish natijasida shina protekt orining chuqurligi 2,3 mm bo‘lgani ma’lum bo‘ldi.
a) 1 km masofa yurilganda shina protektori chuqurligi qanday
o‘zgaradi?
b) 10000 km masofa yurilganda-chi?
5. Madina Qarshi shahridan soat 11:43 da chiqib, soat 15:49 da Guliston shahriga yetib keldi. Agar u 350 km masofa yurgan bo‘lsa, uning o‘rtacha
km
tezligi necha bo‘ldi? soat
Misol. Silindr shaklidagi idish suv bilan bir xil tezlikda to‘ldirilmoqda. Bunda silindrik idish ichiga vaqtga proportsional bo‘lgan suv (hajmi) quyilayotgani bois suv sathining (balandligining) vaqtga nisbatan bog‘lanishi chiziqli funksiya ko‘rinishida bo‘ladi (1-rasmga qarang).
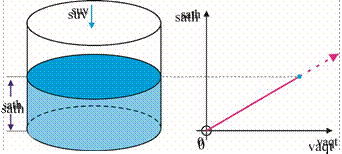
1-rasm.
Bu holda idishdagi suv sathining vaqtga bo‘lgan nisbati (ya’ni sathning o‘zgarish tezligi) o‘zgarmas son bo‘lib qolaveradi.
Endi boshqa shakldagi idishni qaraymiz (2-rasm):
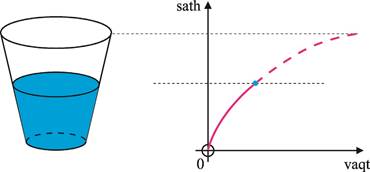
2-rasm.
2- rasmda suv sathining o‘zgarish tezligining vaqtga nisbatan bog‘lanishi aks ettirilgan.
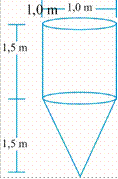
1-savol. 3-rasmda suv quyishga mo‘ljallangan idish tasvirlangan.
 1,5 m
1,5 m
1,5 m
3-rasm.
Boshida unda suv yo‘q edi. Keyin u “bir sekundda bir litr” tezlikda to‘ldirila boshlandi. Suv sathining vaqtga nisbatan o‘zgarishi 4-rasmdagi qaysi grafikda to‘g‘ri ko‘rsatilgan?
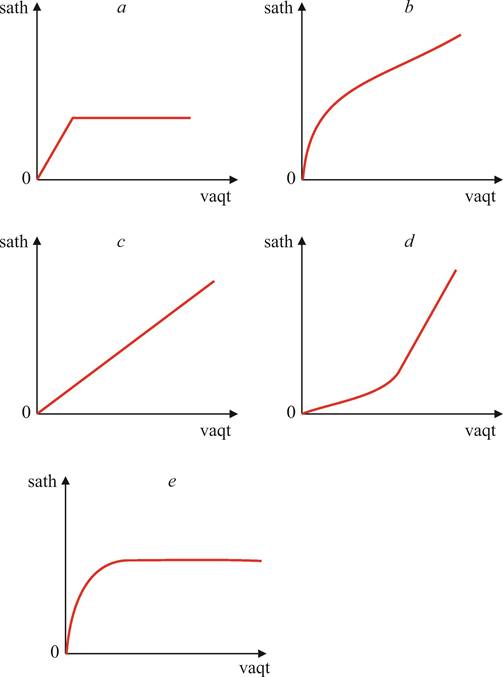
4-rasm.
2-savol. Suv sathining vaqtga nisbatan o‘zgarishi 5-rasmdagi grafiklarda
berilgan:
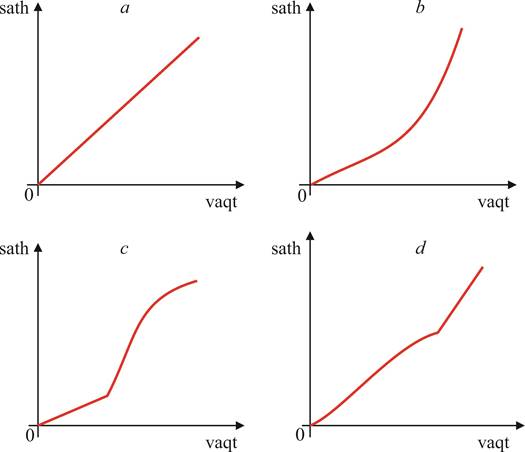
5-rasm.
Ular 6-rasmdagi qaysi idishlarga mos keladi?
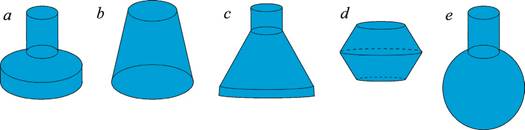
6-rasm.
O‘zgarishning o‘rtacha tezligi
Ikkita o‘zgaruvchi miqdorning bir-biriga bog‘lanishi chiziqli funksiya ko‘rinishida bo‘lsa, bu miqdorlar orttirmalarining nisbati o‘zgarmas son bo‘ladi.
Ikkita o‘zgaruvchi miqdorning bir-biriga bog‘lanishi chiziqli funksiya ko‘rinishida bo‘lmasa, biz bu o‘zgaruvchi miqdorlarning berilgan oraliqdagi o‘rtacha nisbatini topa olamiz. Agar oraliqlar turlicha olinsa, hisoblangan o‘rtacha nisbatlar ham turlicha bo‘ladi.
1-misol. Moddiy nuqtaning vaqtga nisbatan to‘g‘ri chiziq bo‘ylab harakat qonuni grafikda tasvirlangan (7- rasm). FM kesuvchining burchak koeffitsiyentini toping.
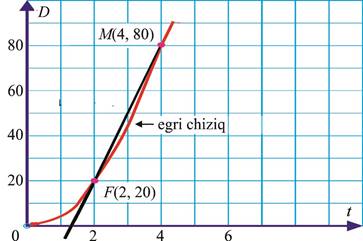
7-rasm.
r Grafikda t=2 sekundga mos bo‘lgan F nuqtani va undan farqli (masalan, t=4 sekundga mos bo‘lgan) M nuqtani belgilaylik. 2 ≤ ≤t 4 vaqt
(80 20)− m m
![]() oralig‘ida o‘rtacha tezlik =30 ga teng ekanligini topamiz.
oralig‘ida o‘rtacha tezlik =30 ga teng ekanligini topamiz.
(4 2)− s s
Ko‘rinib turibdiki, FM kesuvchining burchak koeffitsiyenti 30 ga teng ekan. ▲
Savol. F nuqtani qo‘zg‘almas hisoblab, t ning quyida berilgan qiymatlariga mos bo‘lgan M nuqtalar uchun FM kesuvchilarning burchak koeffitsiyentlarini hisoblab, jadvallarni to‘ldiring:
|
t |
burchak koeffitsiyenti |
|
t |
burchak koeffitsiyenti |
|
0 |
|
3 |
|
|
|
1,5 |
|
2,5 |
|
|
|
1,9 |
|
2,1 |
|
|
|
1,99 |
|
2,01 |
|
Qanday xulosaga keldingiz?
2-misol. Populatsiyadagi sichqonlar soni haftalar kechishi bilan quyidagicha o‘zgaradi (8-rasm):
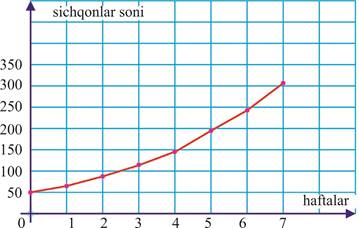
8-rasm.
3- va 6- hafta oralig‘ida sichqonlar soni o‘rtacha qanday o‘zgargan?
7 haftalik vaqt oralig‘da-chi?
r Sichqonlar populatsiyasining o‘sish tezligi
(240 −110)ta sichqon sichqon
![]() ≈ 43 , ya’ni 3- va 6- hafta oralig‘ida
≈ 43 , ya’ni 3- va 6- hafta oralig‘ida
(6 −3)ta hafta hafta
sichqonlar soni haftasiga o‘rtacha 43 taga ko‘paygan.
(315−50)ta sichqon sichqon
![]() Xuddi
shunday 7 haftada ≈ 38 .
Xuddi
shunday 7 haftada ≈ 38 .
(7 − 0)ta hafta hafta
7 hafta oralig‘ida sichqonlar soni haftasiga o‘rtacha 38 taga ko‘paygan. ▲
|
Umumiy holda: x miqdor a dan b gacha o‘zgarganda y=f(x) miqdor o‘zgarishining o‘rtacha tezligi f b( ) − f (a)
b − a orttirmalar nisbatiga teng, bu yerda f (b) – f (a) – funksiya orttirmasi, b – a esa argument orttirmasi. |
f (a
+
−h) f ( )a h=b – a deb
belgilasak, o‘rtacha tezlik ![]() ko‘rinishni oladi.
ko‘rinishni oladi.
h
|
f (a + −h) f ( )a
Kasrning o‘zi esa ayirmali nisbat deb atashadi. |
6. Nuqtaning to‘g‘ri chiziq bo‘ylab yurgan yo‘li vaqtga qanday bog‘langanligi 9-rasmdagi grafikda tasvirlangan.
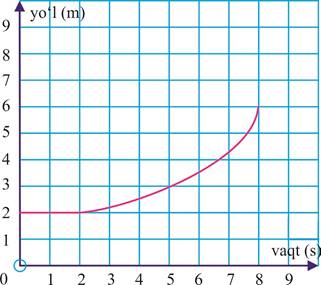
9-rasm.
Nuqtaning
a) dastlabki 4 sekund;
b) so‘nggi 4 sekund;
c) 8 sekund mobaynidagi o‘rtacha tezligini toping.
7. 1) Dalaga turli miqdordagi (dozadagi) dori bilan ishlov berilganda 1 m2 da mavjud bo‘lgan zararli hasharotlar sonining o‘zgarishi 10-rasmdagi grafikda ko‘rsatilgan.
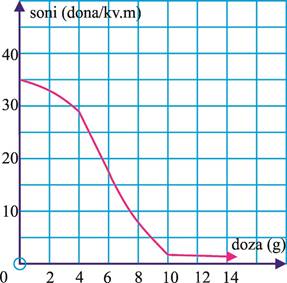
10-rasm.
a) 1) doza 0 grammdan 10 grammgacha oshirilsa; 2) 4 grammdan 7 gramm gacha oshirilsa, 1 m2 da mavjud bo‘lgan zararli hasharotlar sonining o‘zgarishini toping.
b) doza 10 grammdan 14 grammgacha oshirilsa, qanday hodisa ro‘y
beradi?
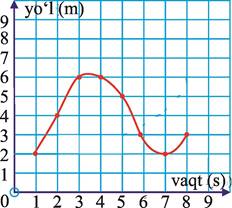
2) Moddiy nuqtaning to‘g‘ri chiziq bo‘yicha harakat qonuni s(t) ning grafigi rasmda berilgan.
a) s(2), s(3), s(5), s(7) sonlar nechaga teng?
b) Qaysi oraliqlarda funksiya o‘suvchi?
c) Qaysi oraliqda funksiya kamayuvchi?
d) s(3)–s(1), s(5)–s(4), s(7)–s(6), s(8)–s(6) orttirmalarni hisoblang.

x ning qiymatlari 2 dan kichik bo‘lib, 2 ga yaqinlasha borganda f(x)=x2
funksiyaning qiymatlari jadvalini qaraylik:
|
x |
1 |
1,9 |
1,99 |
1,999 |
1,9999 |
|
f(x) |
1 |
3,61 |
3,9601 |
≈ 3,996 00 |
≈ 3,999 60 |
Jadvaldan ko‘rinib turibdiki, x ning qiymatlari 2 ga qancha yaqin bo‘lav ersa (yaqinlashsa), f(x) funksiyaning mos qiymatlari ham 4 soniga yaqinlasha-
veradi.
Bunday holatda x argument (o‘zgaruvchi) 2 ga chapdan yaqinlash- ganda f(x) ning qiymatlari 4 soniga yaqinlashadi deymiz.
Endi x ning qiymatlari 2 dan katta bo‘lib, 2 ga yaqinlasha borganida f(x)=x2 funksiyaning qiymatlari jadvalini qaraylik:
|
x |
3 |
2,1 |
2,01 |
2,001 |
2,0001 |
|
f(x) |
9 |
4,41 |
4,0401 |
≈ 4,004 00 |
≈ 4,000 40 |
Bunday holatda x argument 2 ga o‘ngdan yaqinlashganda, f(x) funksiya qiymatlari 4 soniga yaqinlashadi deymiz.
Yuqoridagi ikki holatni umumlashtirib, x argument 2 ga yaqinlashganda, f(x) ning qiymatlari 4 soniga yaqinlashadi deymiz va buni quyidagicha
yozamiz:
limx2 = 4.
x→2
Bu yozuv shunday o‘qiladi: x argument 2 ga yaqinlashganda, f(x) = x2 funksiyaning limiti 4 ga teng.
Umumiy holda funksiya limiti tushunchasiga quyidagicha yondashi- ladi:
|
x≠a bo‘lib, uning qiymatlari a soniga yaqinlashsa, f(x) ning mos qiymatlari A soniga yaqinlashsin. Bu holda A sonni x a ga yaqinlashganda f(x) funk siyan ing limiti deyiladi va bunday belgilanadi: lim f ( x) = A. x→a Ayrim hollarda mazkur holatni x ning qiymatlari a ga intilganda f(x) funksiya A ga intiladi, deymiz. |
lim f ( x) = A yozuv o‘rniga x→a da f(x)→A yozuv ham qo‘llaniladi. x→a
Eslatma. x ning qiymati a ga intilganda x ≠ a sharti bajarilishining muhimligini aytib o‘tish joiz.
Misol. x→0 bo‘lganda f ( )x = 5x + x2 funksiyaning limitini toping.
x
r x
≠ 0 sharti bajarilmasin, ya’ni x=0 bo‘lsin. x=0
qiymatni f(x) ga bevosita qo‘yib ko‘rsak, ![]() ko‘rinishdagi aniqmaslikka ega bo‘lamiz.
ko‘rinishdagi aniqmaslikka ega bo‘lamiz.
Boshqa
tomondan, f ( )x =
![]() x(5+
x) bo‘lgani uchun bu funksiya ushbu x
x(5+
x) bo‘lgani uchun bu funksiya ushbu x
5+ x, agar x ≠ 0 bo‘lsa f x( ) =
aniqlanmagan, agar x ≠= 0 bo‘lsa,
ko‘rinishni oladi. y=f(x) funksiyaning grafigi (0; 5) koordinatali nuqtasi “olib tashlangan” y=x + 5 to‘g‘ri chiziq ko‘rinishida bo‘ladi (11-rasm):
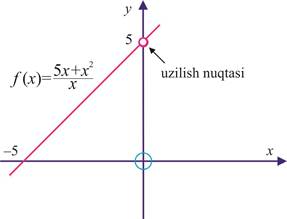
11-rasm.
(0; 5) koordinatali nuqta y = f(x) funksiyaning uzilish nuqtasi deyiladi.
Ko‘rinib turibdiki, bu nuqtadan farqli bo‘lgan nuqtalarda x ning qiymatlari 0 ga yaqinlashganda f(x) funksiyaning mos qiymatlari 5 ga yaqinlashadi, ya’ni uning limiti mavjud: lim5x + x2 = 5. ▲
x→0 x
Amalda, funksiya limitini topish uchun, lozim bo‘lsa, tegishli soddalashtirishlarni bajarish maqsadga muvofiq.
1-misol. Limitlarni hisoblang:
2 x2 +3x x2 −9 .
a) limx ; b) lim ; c) lim
x→2 x→0 x x→3 x −3
r a) x ning qiymatlari 2 ga yaqinlashganda x2 ning qiymatlari 4 ga yaqin lashadi, ya’ni limx2 = 4.
x→2
b) x ≠ 0 bo‘lgani uchun x2
+ 3x x
x(
+
3)
. lim = lim
![]() = lim(xx+
=3)
3
= lim(xx+
=3)
3
x→0 x x→0 x x→0
c) x ≠ 3 bo‘lgani uchun
![]() x2 −9
x2 −9
lim = lim. ▲
x→3 x −3 x→3 x −3 x→3
Mashqlar Limitni hisoblang (8–11):
8. a) lim( x + 4); b) lim(5− 2 x) ; c) lim(3x −1)
x→3 x→−1 x→4
d) lim(5x2 − +3x 2) ; e) limh2 (1− h) ; f) lim( x2 + 5).
x→2 h→0 x→0
9. a) lim5; b) lim7 ; c) lim ,c c – o‘zgarmas son.
x→5 h→2 x→0
10. a) lim x2 − 3 x ; b) lim h2 + 5h ; c) lim x −1 ; d) lim x .
x→1 x h→2 h x→0 x +1 x→0 x
2 2 2
11. a) lim x −3x ; b) lim x −5x ; c) lim2x −x .
x→0 x x→0 x x→0 x
d) lim 2h2 + 6h ; e) lim3h2 − 4h ; f) lim h3 −8h;
h→0 h h→0 h h→0 h
g) lim x2 − x; h) lim x2 − 2 x ; i) lim x2 − −x 6.
x→1 x −1 x→2 x − 2 x→3 x −3
12. Quyidagi funksiyalardan qaysi biri x→3 da limitga ega? Shu limitni toping.
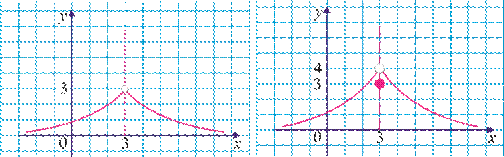
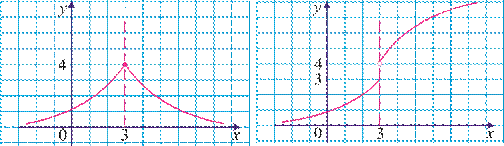
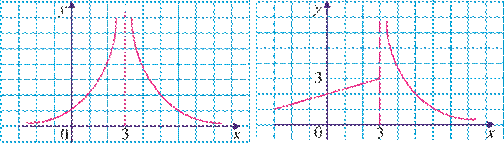
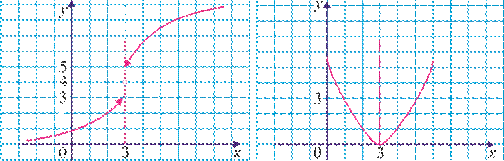
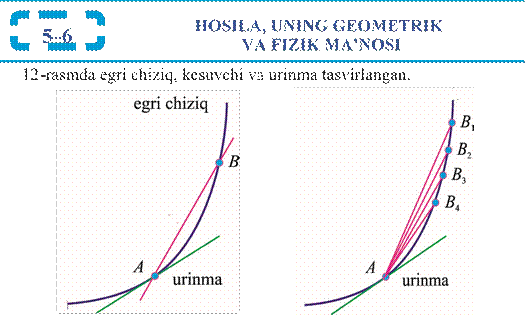
12-rasm. 13-rasm.
B nuqta B1, B2, ... holatlarni ketma-ket qabul qilib, A nuqtaga egri chiziq bo‘ylab yaqinlashsa (13-rasm), mos kesuvchilarning egri chiziqqa A nuqtada o‘tkazilgan urinma holatini olishga intilishini intuitiv tarzda qabul qilamiz.
Bu holda, ravshanki, AB to‘g‘ri chiziqning burchak koeffitsiyenti urinmaning burchak koeffitsiyentiga yaqinlashadi.
1-misol. f(x) = x2 funksiyaning grafigiga A(1; 1) nuqtada urinadigan to‘g‘ri chiziqning burchak koeffitsiyentini toping (14-rasm).
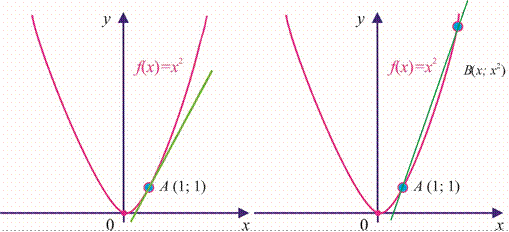
14-rasm. 15-rasm.
r f(x) = x2 funksiyaning grafigiga tegishli ixtiyoriy B(x, x2) nuqtani qaraylik (15-rasm).
AB to‘g‘ri chiziqning burchak koeffitsiyenti
f ( x) − f (1) yoki x2 −1 ga teng.
![]()
x −1 x −1
B nuqta A nuqtaga egri chiziq bo‘ylab yaqinlashganda, x ning qiymati 1 ga yaqinlashadi, bunda x ≠ 1.
Demak, AB to‘g‘ri chiziqning burchak koeffitsiyenti urinmaning burchak koeffitsiyenti k ga yaqinlashadi, ya’ni:
k = lim
x2 −1
=
lim
![]() ( x +1)(
x −1) =
lim(
x + =1) 2.
( x +1)(
x −1) =
lim(
x + =1) 2.
x→1 x −1 x→1 x −1 x→1
Shunday qilib, k = 2. ▲
y = f(x) funksiya berilgan bo‘lsin. Uning grafigiga tegishli bo‘lgan A(x; f(x)) va B(x+h; f (x+h)) nuqtalarni qaraylik (16-rasm). AB to‘g‘ri chiziqning burchak koeffitsiyenti
f ( x + −h) f ( x) f ( x + −h) f ( x)
![]() =
=
x + −h x h
ayirmali nisbatga teng.
B nuqta A nuqtaga egri chiziq bo‘ylab yaqinlashganda h→0, ya’ni h orttirma nolga intiladi, AB kesuvchi esa funksiya grafigiga A nuqtada o‘tkazilgan urinmaga intiladi.
Shu bilan birga, AB to‘g‘ri chiziqning burchak koeffitsiyenti urinmaning burchak koeffitsiyentiga yaqinlashadi.
Boshqacha aytganda, h ning qiymati 0 ga intilganda ixtiyoriy (x; f(x))
nuqtada o‘tkazilgan urinmaning burchak
koeffitsiyenti ![]() f (
x + −h ) f
( x ) h
f (
x + −h ) f
( x ) h
f (x
+
−h) f ( )x ayirmali nisbatning limit qiymatiga, ya’ni lim![]() qiymatga teng
qiymatga teng
h→0 h
bo‘ladi.
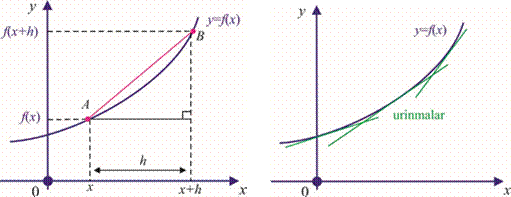
16-rasm. 17-rasm.
x ning mazkur limit mavjud bo‘lgan ixtiyoriy qiymatiga funksiya grafigiga (x, f (x)) nuqtada o‘tkazilgan urinmaning burchak koeffitsiyentining yagona qiymatini mos qo‘yish mumkin (17-rasm).
f ( x + −h) f ( x)
Demak, lim ![]() formula yangi funksiyani ifodalaydi.
formula yangi funksiyani ifodalaydi.
h→0 h
Mana shu funksiya y=f (x) funksiyaning hosilaviy funksiyasi, yoki sodda qilib hosilasi deb ataladi.
|
Ta’rif. y=f (x) funksiyaning hosilasi deb quyidagi limitga (agar u mavjud bo‘lsa) aytiladi: f ( x + −h) f ( x) lim h→0 h Odatda y=f (x) funksiyaning hosilasi f ʹ(x) kabi belgilanadi. Hosilani topish amali differensiallash deyiladi. |
dy
f ʹ(x) belgilash
o‘rniga ![]() kabi belgilash ham
qabul qilingan. dx
kabi belgilash ham
qabul qilingan. dx
Bu belgilashning “kasr” ko‘rinishda ekanligini quyidagicha tushuntirish mumkin.
Agar orttirmalarni h= Δx, f(x+Δx) – f(x)=Δy deb belgilasak,
f (x + h) − f ( )x
f ′( )x =
lim ![]() dan quyidagiga ega bo‘lamiz (18-
dan quyidagiga ega bo‘lamiz (18-
h→0 h
∆y dy
![]() rasm): f ′(
)x = lim = .
rasm): f ′(
)x = lim = .
∆ →x 0 ∆x dx
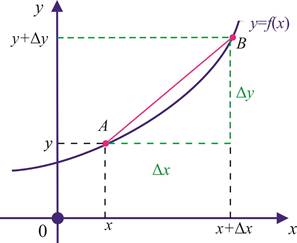
18-rasm.
Yuqoridagi mulohazalardan shunday xulosaga kelamiz: y = f(x) funksiya hosilasining x0 nuqtadagi qiymati funksiya grafigiga shu nuqtada o‘tkazilgan urinmaning burchak koeffitsiyentiga teng. Hosilaning geometrik ma’nosi shundan iboratdir.
2-misol. Moddiy nuqta s=s(t) (s – metrlarda, t – sekundlarda o‘lchanadi) qonunga muvofiq to‘g‘ri chiziq bo‘ylab harakat qilmoqda. Shu moddiy nuqtaning vaqtning t momentidagi (paytidagi) tezligi v(t) ni toping.
r Ma’lumki, oniy tezlik nuqtaning kichik vaqt oralig‘i Δt dagi o‘rtacha tezligi v t( ) s t( t) s t( ) ga taqriban teng. Δt nolga intilganda oniy tezlik va t
o‘rtacha tezlik orasidagi farq ham nolga intiladi. Demak, moddiy nuqtaning t momentdagi oniy tezligi
v t( ) lim s t( t) s t( ) lim s s t'( ).▲
t0 t t0 t
Shunday qilib, t momentdagi oniy tezlik nuqtaning harakat qonuni s(t) funksiyadan olingan hosilaga teng ekan.
Hosilaning fizik ma’nosi ana shundan iborat. Umuman aytganda, hosila funksiyaning o‘zgarish tezligidir.
Hosila ta’rifidan foydalanib, funksiyalarning hosilasini toping:
|
1. f (x)=x2; 2. f (x)=5; |
3. f (x)=x3–7x+5; |
|
|
4. f (x)=x4; 5. f ( )x = 1 ; |
|
|
x
r 1. h≠0 bo‘lgani uchun
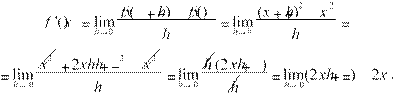
2. h ≠ 0 bo‘lgani uchun f (x+h)=5, f (x+h)– f(x)=5 – 5=0,
![]() f
(x
+
−h) f ( )x =
=0 0 Demak, f ′(
x) = lim
f
(x
+
−h) f ( )x =
=0 0 Demak, f ′(
x) = lim
![]() f (
x + h)
−
f
(
x) = 0. h h h→0 h
f (
x + h)
−
f
(
x) = 0. h h h→0 h
3. h≠0 bo‘lgani uchun f (x+h)=(x+h)3 – 7 (x + h) + 5 = x3 + 3x2h + 3xh2 + h3 – 7x – 7h + 5; f (x+h) – f (x)=x3 + 3x2h + 3xh2 +h3 – 7x – 7h + 5 – x3 + 7x – 5 = =3x2h+3xh2+h3 – 7h.
![]() f
(x + −h) f ( )x = 3x h2 +3xh2 + −h3 7h =3x2+3xh+h2 – 7. h h
f
(x + −h) f ( )x = 3x h2 +3xh2 + −h3 7h =3x2+3xh+h2 – 7. h h
h →0 da 3xh+h2 →0 bo‘lgani uchun
f (
x + h)
−
f
(
x) f ′( x) =
lim
![]() =3x2–7.
=3x2–7.
h→0 h
4. Qisqa ko‘paytirish formulalariga ko‘ra a4 – b4=(a – b)(a + b)(a2 + b2). Demak, (x+h)4 – x4=(x+h–x)(x+h+x)((x+h)2+x2)=
=h(2x+h)(2x2+2xh+h2)=2hx(2x+h)(x+h)+h3(2x+h)=
=2hx(2x2+h(3x+h))+h3(2x+h); h→0 bo‘lsa,
2h2x(3x+h) → 0 va h3(2x+h) → 0 bo‘lgani uchun
![]() (x
+
−h)4 x4
3 2(2x
+ h))=4x3. lim = lim(4x
+
2hx(3x
+
+h))
h
(x
+
−h)4 x4
3 2(2x
+ h))=4x3. lim = lim(4x
+
2hx(3x
+
+h))
h
h→0 h h→0
Demak, f ʹ(x)=(x4)ʹ=4x3.
5. f ( x) = 1 , x ≠ 0 bo‘lsin,
x
![]() 1 1 x
−
+(
x h) h
1 1 x
−
+(
x h) h
f ( x + −h) f ( x) = − = =− ,
x + h x ( x + h x) ( x + h x)
f ( x + −h) f ( x) – 1
![]() = .
h ( x + h
x)
= .
h ( x + h
x)
h → 0 da x+h→x bo‘lgani uchun f ′( )x = − 1 bo‘ladi.
x2
6.
![]()
![]() f (
x) = x ,
x > 0, x +
>h 0 bo‘lsin, f ( x +
−h) f ( x) =
x
+
−h x
f (
x) = x ,
x > 0, x +
>h 0 bo‘lsin, f ( x +
−h) f ( x) =
x
+
−h x
h h
ayirmali nisbatni tuzamiz va uni soddalashtiramiz:

Javob: 1. 2x. 2. 0. 3. 3x2 – 7. 4. 4x3. 5. −
![]() 12 . 6. 1 . 7. 31 2 .▲
12 . 6. 1 . 7. 31 2 .▲
![]() x 2 x 3 x
x 2 x 3 x
|
Eslatish joizki, x miqdor x dan x+h gacha o‘zgarganda y=f (x) miqdor o‘zgarishining o‘rtacha tezligi f ( x + h) − f ( x)
h ayirmali nisbatga teng. f ( x + h) − f ( x) Bundan lim h→0 h oniy tezligini bildiradi. |
13. Quyidagi funksiyaning hosilasi nimaga teng?
![]()
a) f (x)=x3; b) f (x)=x–1; c) f (x)= x; d) f (x)=c.
14. Jadvalni daftaringizga ko‘chiring va to‘ldiring:a)
|
f(x) |
f ʹ(x) |
|
x1 x2 x3 x–1 x |
|
b) Fikringizcha, y=xn funksiya hosilasi nimaga teng (bu yerda n –
ratsional son) ?
15. Ta’rifdan foydalanib, funksiya hosilasini toping:
a) f (x)=2x + 3; b) f (x)=3x2 + 5x + 1; c) f (x)=2x3 + 4x2+6x – 1.
16*. Daftaringizga ko‘chiring va to‘ldiring:
a) f (x)=ax + b uchun f ʹ(x) = ...;
b) f (x)=ax2 + bx +c uchun f ʹ(x) = ...;
c) f (x)=ax3 + bx2 + cx + d uchun f ʹ(x) = ...
17*. Quyidagi tasdiqlarni isbotlang:
a) f (x) = cg(x) bo‘lsa, u holda f ʹ(x) = cg ʹ(x);
b) f (x) = g(x) + h(x) bo‘lsa, u holda f ʹ(x) = gʹ(x) + hʹ(x).
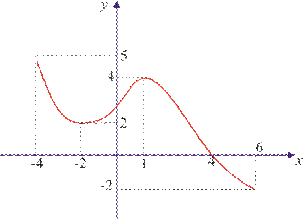
18*. Funksiya grafigiga qarab hosilalar qiymatlarini solishtiring:
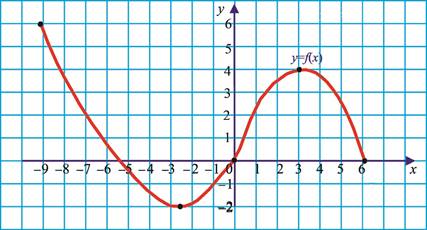
a) f ʹ(–7) va f ʹ(–2); c) f ʹ(–9) va f ʹ(0);
b) f ʹ(–4) va f ʹ(2); d) f ʹ(–1) va f ʹ(5).
19. 1) Yuqoridagi funksiya grafigiga qarab ushbu shartlarni qanoat lanti- radigan x1, x2 nuqtalarni toping (x1, x2 – Ox o‘qidagi nuqtalar: –9, –8, ..., 5, 6):
a) f ʹ(x1) > 0, f ʹ(x2) > 0; b) f ʹ(x1) < 0, f ʹ(x2) > 0;
c) f ʹ(x1) < 0, f ʹ(x2) < 0; d) f ʹ(x1) > 0, f ʹ(x2) < 0.
2) Grafikka qarab ushbu savollarga javob bering:
a) funksiya qaysi oraliqda o‘suvchi? qaysi oraliqda kamayuvchi?
b) funksiyaning [0; 3], [3; 6], [–9; –6] oraliqlaridagi orttirmalarini
hisoblang.
3) Funksiya qaysi nuqtada eng katta, qaysi nuqtada eng kichik qiymatni qabul qiladi?
4) Funksiya qaysi nuqtalarda nolga aylanyapti?
5) Qaysi oraliqda funksiya musbat qiymatlarni qabul qilyapti?
6) Qaysi oraliqda funksiya manfiy qiymatlarni qabul qilyapti?

Agar f(x) va g(x) funksiyalarning har biri hosilaga ega bo‘lsa, u holda quyidagi differensiallash qoidalari o‘rinlidir:
|
1. Yig‘indining hosilasi hosilalar yig‘indisiga teng: (f(x) + g(x))' = f '(x) + g'(x). |
|
|
|
|
|
(1) |
|
2. Ayirmaning hosilasi hosilalar ayirmasiga teng: (f(x) – g(x))' = f '(x) – g'(x). |
|
|
|
|
|
(2) |
1-misol. Funksiyaning hosilasini toping:
1) f(x)=x3+x2 –x+10; 2) f
x(
) =
![]() .
.
r Hosilani topishda 1, 2-qoidalaridan va hosilalar jadvalining 1, 3- bandlaridan foydalanamiz, ya’ni:
1) f ′( )x = (x3)′+(x2)′−( )x ′+10 = 3x2 + 2x −1;
2)
![]() f
'(
)x = x
f
'(
)x = x![]() 12
′
− x− 1 ′
= 1
−
12
+
1
x−
23.
12
′
− x− 1 ′
= 1
−
12
+
1
x−
23.
2 x
2 2
1 3
2
![]() 1
−
2
+
1
x−
2.▲
1
−
2
+
1
x−
2.▲
Javob: 1) 3x + 2x −1; 2) x
2 2
3. O‘zgarmas ko‘paytuvchini hosila belgisidan tashqariga chiqarish
mumkin:
(cf(x))'=c∙f ' (x), c – o‘zgarmas son. (3)
2-misol. Funksiyaning hosilasini toping:
![]() 1) f(x)
= 7x3–5x2+4; 2) f
x(
) =33 x + −5
x3. x
1) f(x)
= 7x3–5x2+4; 2) f
x(
) =33 x + −5
x3. x
r Hosilani topishda 1, 2, 3-qoidalaridan va hosilalar jadvalining 1, 3- bandlaridan foydalanamiz, ya’ni:
1) f ′( )x = (7x3 −5x 2 +4)' = (7x3)'−(5x2 )' (4)'+ = 21x2 −10x;
''
2)
![]()
![]()
![]()
![]() f
′(x)
=
3
x + 5x −
x3
= 3()'
+
5·
1x
− (x3)'
= 23x −
x52 −3x2.
f
′(x)
=
3
x + 5x −
x3
= 3()'
+
5·
1x
− (x3)'
= 23x −
x52 −3x2.
2 3 − −5 3x2. ▲
![]() Javob: 1) 21x
−10x;; 2) 2 x x2
Javob: 1) 21x
−10x;; 2) 2 x x2
|
4. Ko‘paytmaning hosilasi: ( f(x)g(x))'=f '(x)g(x)+f(x)g'(x). |
|
|
|
|
|
|
(4) |
3- misol. Funksiyaning hosilasini toping:
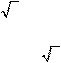
1) f(x)=(2x+4)(3x+1); 2) f(x) = (3x2+4x+1)(2x+6); 3) f (
)![]() ( 5 ) .
( 5 ) .
r Hosilani topishda 1, 3, 4-qoidalaridan va hosilalar jadvalining 1-, 3- bandlaridan foydalanamiz, ya’ni:
1) f ′( )x = ((2x + 4)(3x +1))' = (2x + 4)'(3x +1)+(2x + 4)(3x +1)'=
= 2(3x +1)+3(2x + 4) = 6x + 2+6x +12 =12x +14;
2) f '( )x = ((3x2 + 4x +1)(2x +6))' = (3x2 + 4x +1)'(2x +6)+
+(3x2 + 4x +1)(2x +6)' = (6x + 4)(2x +6)+ 2(3x2 + 4x +1) =18x2 +52x + 26.;
 Javob:
Javob: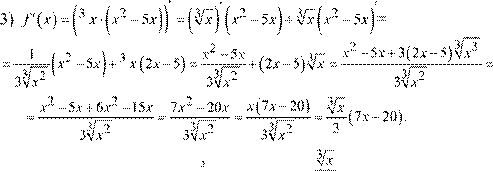 1) 12x
+14;; 2) 18x +52x
+
26.; 3) (7x−
20 .)
▲ 3
1) 12x
+14;; 2) 18x +52x
+
26.; 3) (7x−
20 .)
▲ 3
|
5. Bo‘linmaning hosilasi:
g x( ) ( ( ))g x |
bunda g(x) ≠ 0. (5) |
![]() 4- misol. Funksiyaning
hosilasini toping: x +1 3x
+7
4- misol. Funksiyaning
hosilasini toping: x +1 3x
+7
1) f
x(
) =
![]() ; 2) f x( ) =
; 2) f x( ) =
![]() ; 3) f
x(
) =
. x −2
x −5 5x
−
7
; 3) f
x(
) =
. x −2
x −5 5x
−
7
r Hosilani topishda 1, 3, 5-qoidalaridan va hosilalar jadvalining 1, 3- bandlaridan foydalanamiz, ya’ni:
x +1 ′ (x +1)'(x −2)−(x +1)(x −2)' x −2−(x +1) 3
1)
![]() f '( )x =
x −2
= (x
−2)2 = (x
−2)2 =
− (x
−2)2 ;
f '( )x =
x −2
= (x
−2)2 = (x
−2)2 =
− (x
−2)2 ;
3x +7 ′ (3x +7)'(x −5)−(3x +7)(x −5)'
2)
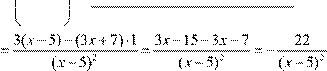 f '( )x =
f '( )x = ![]() = 2 =
x
−5 (x
−5)
= 2 =
x
−5 (x
−5)
;
![]() x ′ (
x) (5′⋅ x −
7)
− x
⋅(5x
−
7)′
x ′ (
x) (5′⋅ x −
7)
− x
⋅(5x
−
7)′
3) f ′( )x = = 2 ==
5x − 7 (5x − 7)
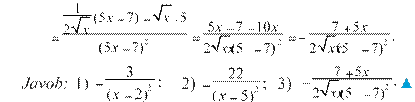
5- misol. Funksiyalarning hosilasini toping:
1) f(x) = sinx; 2) f(x) = cosx; 3) f(x) = tgx .
r 1) Ayirmali nisbatni topishda sinuslar ayirmasini ko‘paytmaga keltirish formu lasidan foydalanamiz:
h 2x h+ h
2sin cos sin
![]() sin(x h+ ) −sin
x = 2 2 = 2
cos 2x h+ . h h h 2
sin(x h+ ) −sin
x = 2 2 = 2
cos 2x h+ . h h h 2
2
2x + h
![]() h→0 da →1, scos
h→0 da →1, scos ![]() → cosx ekanini isbotlash mumkin.
h 2
→ cosx ekanini isbotlash mumkin.
h 2
2
Demak, (sinx)'=cosx.
2) Ayirmali nisbatni topishda kosinuslar ayirmasini ko‘paytm aga keltirish formu lasidam foydalanamiz:
h 2x h+ h h
2sin sin sin sin
![]()
![]() .
.
2 2
h h→0 da; sin(x+ ![]() ) →
sin
x ekanini
isbotlash mumkin. 2
) →
sin
x ekanini
isbotlash mumkin. 2
Demak, (cosx)' = – sinx .
3) Hosilani topishning 5-qoidasi hamda shu misolning 1-, 2-qism sin x
javoblaridan
foydalanib, f x( ) =
tgx
= ![]() funksiyaning hosilasini topamiz: cosx
funksiyaning hosilasini topamiz: cosx
'
' sinx (sinx)' cosx − sinx(cosx)'
![]() f
′(x)
=((tgtgxx)) =
cosx
= cos2 x =
f
′(x)
=((tgtgxx)) =
cosx
= cos2 x =
cos cosx x − sinx(−sinx) cos2 x + sin2 x 1
![]() = = = .
= = = .
2 2 2
cos x cos x cos x
Javob: 1) (sinx)'=cosx; 2) (cosx)'
= – sinx; 3) (tgx)′ =
![]() 12 . ▲ cos
x
12 . ▲ cos
x
Hosilani hisoblashda differensiallash qoidalari va quyidagi jadvaldan foydalanish maqsadga muvofiqdir.
Hosilalar jadvali
|
№ |
Funksiyalar |
Hosilalar |
|
1 |
c – o‘zgarmas |
0 |
|
2 |
kx+b, k, b – o‘zgarmaslar |
k |
|
3 |
xp, p – o‘zgarmas |
pxp–1 |
|
4 |
sinx |
cosx |
|
5 |
cosx |
– sinx |
|
6 |
tgx |
1
cos2 x |
|
7 |
ctgx |
|
|
8 |
ax, a>0 |
ax lna |
|
9 |
ex |
ex |
|
10 |
lnx |
1/x |
|
11 |
lgx |
1
x⋅ln10 |
|
12 |
loga x, a>0, a=1 |
1
x⋅lna |
1. Hosilani hisoblash qoidalarini ayting. Har bir qoidaga misolkeltiring.
2. Hosilalar jadvalining 4-, 5- bandlarini isbotlang.
3. Funksiyaning x=x0 nuqtadagi hosilasi nima-yu, hosilaviy funksiya nima? Ularning qanday farqi bor? Misollarda tushuntiring.
Hosilani toping (20–22):
![]()
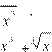 4; 2) y = 12
; 3) y = 1 20. 1) y = x
4; 2) y = 12
; 3) y = 1 20. 1) y = x
x
1
21. 1) y = x4 – x2+x; 2) y = + x ; 3) y = ; x
4 3 2 1 1
![]() 4)
y = x + x
+
x
−
x
− −
2 .
4)
y = x + x
+
x
−
x
− −
2 .
x x
x2 − 4
22. 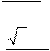 1) y =
(x –
1)(x2–5); 2) y
=; x − 2
1) y =
(x –
1)(x2–5); 2) y
=; x − 2
![]() 3) y=(x4
−
x
x)(
2
+x); 4) y =
x +1
. x −1
3) y=(x4
−
x
x)(
2
+x); 4) y =
x +1
. x −1
23. Moddiy nuqtaning berilgan t0 vaqtdagi tezligini hisoblang:
1) ![]() s(t) = t3–2t2+t; t0 = 5; 2) s(
)t = 5t +t3 +
t
, t0=4.
s(t) = t3–2t2+t; t0 = 5; 2) s(
)t = 5t +t3 +
t
, t0=4.
24. Funksiyaning abssissasi berilgan nuqtadagi hosilasini hisoblang:
1) f
(x) =
x2 +
5x −3, x0
=1; 3) f (x) =
2
x + x3
+
![]() , x0
=
4; 2) f (x) =
4
−
3x
, x0 =
−2;
4) f (x) = x2+lg2, x0
=1.
, x0
=
4; 2) f (x) =
4
−
3x
, x0 =
−2;
4) f (x) = x2+lg2, x0
=1.
Hosilani toping (25–29):
4 x
25. ![]() 1) y=
2x3–4x2+5; 3) y= +
; x 4
1) y=
2x3–4x2+5; 3) y= +
; x 4
22 1
![]() 2)
y= 7x − 2x
+
7
; 4) y= x
+ .
2)
y= 7x − 2x
+
7
; 4) y= x
+ .
|
|
x2 |
|
26. 1) y=(x–2) (x+2);
|
x2 −9 3) y = x −3 |
2) y=(x+2)3; 4)
y=x2+lg7+ sin![]() .
.
|
27. 1) y = x8 + 7x2 + 5x; |
2) y=2x8+ x6; |
|
x4 3) y = x −1 |
x2 + x +1 4) y = |
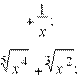 5) y = x−2 6) y = x4 – 4x;
5) y = x−2 6) y = x4 – 4x;
7) y = 8) y = (x5 + x–5)(x2 + x–2).
![]() 28. 1) f (x) =
x5
+
5x4
+
4x3
+
3x2
+
2x
+1; 2) f (x) =
sin2
x+cos2
x ;
28. 1) f (x) =
x5
+
5x4
+
4x3
+
3x2
+
2x
+1; 2) f (x) =
sin2
x+cos2
x ;
|
x 3) f (x)
= cos x |
4) f(x)=tgx; 5) y = 8x ; |
|
6) y = log2 x + log2 3; |
7) y = 2x x ; 8) y = xlnx; |
|
9) y = ex cosx; |
1 10) y =
2ex
− ln x + x |
|
29. 1) y=2xsinx; |
2) y = ex(cosx+sin x); 3) y = xtgx; |
|
ln x 4) y= x |
|
7) y = (x
+1)(ln
x +1) ; ![]() 8) y = (2+
x)3; 9) y=(3x+5)6+2019.
8) y = (2+
x)3; 9) y=(3x+5)6+2019.
30. Moddiy nuqtaning berilgan t0 vaqtdagi tezligini toping:
1) s(t) = t2
+5t
+1, t0 =1; 2) s(t)
=
4t3
+ 1![]() +1, t0 =1.
+1, t0 =1.
t
31. Funksiyaning berilgan nuqtadagi hosilasini toping:
1)
f (x) =
(x+1)3, x0 =−1; 2) f (x)
=
sin
x, x0 =
![]() .
.
32. Hosilani toping:
1) ![]()
![]()
![]() y =
2sin
x; 2) y = 3
−tgx; 3) y=–3cosx; 4) y=tgx–ctgx;
y =
2sin
x; 2) y = 3
−tgx; 3) y=–3cosx; 4) y=tgx–ctgx;
2x
 5) y
=
4x
−
cos
x ; 6) y
=
x
sin
x; 7) y = ; 8) y = xsin
x + cos x . sin x
5) y
=
4x
−
cos
x ; 6) y
=
x
sin
x; 7) y = ; 8) y = xsin
x + cos x . sin x
33. Funksiyaning x0 nuqtadagi hosilasini hisoblang:
1) f
(x)
=
![]() , x0
=
2; 2) f(x) = tgx – x +
2, x0 =
, x0
=
2; 2) f(x) = tgx – x +
2, x0 =
![]() ; 3) f
(x)
=
x(lg
x −1) , x0=10; 4) f(x) = tgx −
; 3) f
(x)
=
x(lg
x −1) , x0=10; 4) f(x) = tgx −![]() lnx, x0 =
lnx, x0 =
![]() .
.
34. Нosilani nolga aylantiradigan nuqtani toping:
|
1) f (x) = x4 −4x; |
2) f (x) = tgx–x; |
|
3) f (x) = x8 − 2x4 + 3; |
x 4) f x( ) =
log2
x− |
ln2

Murakkab funksiya. y = (x2 + 3x)4 funksiyani qaraylik. Agar biz g(x) = x2 + 3x, f(x) = x4 belgilashlarni kiritsak, y = (x2 + 3x)4 funksiya y = f(g(x)) ko‘rinishini oladi. Biz y = f(g(x)) funksiyani murakkab funksiya deymiz.
1-misol. Agar f(x) = x2 va g
x(
)=
![]() x−2 bo‘lsa, quyidagilarni toping: x+3
x−2 bo‘lsa, quyidagilarni toping: x+3
1) f(g(2)); 2) f(g(–4)); 3) g(f(1)); 4) f((–4)); 5) f ( f (1)) 6) g(g(–1)).
r Berilgan funksiyalardan foydalanib, hisoblashlarni bajaramiz:
1)
f g x( ( ))
= f
xx−− 23 , bundan f
g(
(2)) =
f
![]() 22−+23=
f
(0)
=
02 =
0;
22−+23=
f
(0)
=
02 =
0;
− −4 2
2)
f g( ( 4))− = f ![]() = f (6) = 62
= 36 ;
= f (6) = 62
= 36 ;
− +4 3
3)
g f( (1))=
g(1
)2
=
g(1)= ![]() =−
;
=−
;
4)
g f( ( 4))−
= g((–4)
)2
=
g(16)= ![]() =
;
=
;
5) f f( (1)) = f (1 )2 = f (1) = =12 1;
3
− −2
6)
![]() g g(
( 1))− =
g
g g(
( 1))− =
g![]() −
−1 2
=
g−
3
=
2 =
−3,5
=−
7
.
−
−1 2
=
g−
3
=
2 =
−3,5
=−
7
.
−
+1 3
2
− +![]() 3 1,5 3
3 1,5 3
![]()
![]()
![]()
![]()
![]() Javob:
1) 0; 2) 36; 3) −
Javob:
1) 0; 2) 36; 3) −![]() ; 4)
; 4) ![]() ; 5) 1; 6) −
; 5) 1; 6) −![]() . ▲
. ▲
Murakkab funksiyaning hosilasi uchun ushbu formula o‘rinli:
(f (g(x)))=f (g(x))·g'(x) (1)
2-misol. Funksiyaning hosilasini toping (k, b – o‘zgar mas sonlar):
1) f(x) = (kx + b)n; 2) f(x) = sin(kx + b); 3) f(x) = cos(kx + b); 4) f(x) = tg(kx + b).
r 1) f(t) = tn va t(x) = kx + b funksiyalarga (1) formulani qo‘llaymiz:
((kx+b)n)′ = (tn)′ ∙ (kx+b)′ = ntn–1∙k = n∙k∙(kx + b)n–1 .
2) f(t)=sint va t(x) =kx+b funksiyalarga (1) formulani qo‘llaymiz:
(sin(kx+b))′ = (sint)′ ∙ (kx+b)′ = k ∙ cost = k ∙ cos(kx + b).
3) f(t) = cost va t(x) = kx + b funksiyalarga (1) formulani qo‘llaymiz:
(cos(kx + b))′ = (cost)′∙ (kx+b)′ = –k ∙ sint = – k ∙ sin(kx + b).
4) f(t) = tgt va t(x) = kx+b funksiyalarga (1) formulani qo‘llaymiz:
1 k
![]() (tg(kx
+ b))′ = (tgt)′∙ (kx + b)′
= 2
⋅k
= 2 .
(tg(kx
+ b))′ = (tgt)′∙ (kx + b)′
= 2
⋅k
= 2 .
cos t cos (kx +b)
Javob: 1) ((kx + b)n)′ = n∙k∙(kx + b)n–1; 2) (sin(kx + b))′ = k∙cos(kx+b);
k
3) (cos(kx+b)′=–k∙sin(kx+b); 4)
(tg(kx+b)′== ![]() 2 .▲ cos
(kx
b+
)
2 .▲ cos
(kx
b+
)
3-misol. f(x) = sin8x∙e(3x+2) funksiya hosilasini toping.
r Hosilani topishning 4-qoidasi hamda (1) formulani qo‘llab hosilani topamiz:
f ′ (x) = (sin8xe(3x+2))′ = (sin8x)′ e3x+2 + sin8x ∙ (e3x+2)′ = cos8xe3x+2 ∙ (8x)′ + + sin8xe3x+2 ∙ (3x+2)′ = e3x+2 ∙ (8cos8x + 3sin8x).
Javob: e3x+2 ∙ (8cos8x + 3sin8x). ▲
4-misol. h(x) = (x3 + 1)5 funksiyaning x0 = 1 nuqtadagi hosilasini toping.
r (1) formuladan foydalanib hosilani hisoblaymiz: h′(x) = 5(x3+1)4(x3+1)′ = 5(x3+1)43x2 = 15x2(x3+1)4.
Demak, h′(1) = 15(13+1)4·12 = 15·16 = 240. Javob: 240. ▲
5-misol. f(x) = 2cosx funksiyaning hosilasini toping. r (1) formuladan foydalanib hosilani hisoblaymiz:
f ′(x)=2cosxln2(cosx)′ = –sinx2cosxln2. Javob: –sinx2cosxln2.▲
6-misol. f(x) = tg5x funksiyaning hosilasini toping.
r (1) formuladan foydalanib hosilani hisoblaymiz:
4x(tgx)′ = 5tg4x cos12 x . f ′(x)=5tg
5tg4x
Javob: ![]() 2 .▲
2 .▲
cos x
7-misol. h(x)=3cosx·log7(x3+2x) funksiyaning hosilasini toping.
r f (x)=3cosx va g(x)=log7(x3+2x) belgilashlarni kiritib, (1) formulani – murakkab funksiya hosilasini topish formulasini qo‘llaymiz:
f ʹ(x)=(3cosx)ʹ=3cosxln3·(cosx)ʹ=–3cosxln3·sinx,
![]() 3x2
+
2
3x2
+
2
gʹ(x)=(log7(x3+2x))ʹ= ·(x3+2x)ʹ= ![]() 3
3
(x + 2 )x ln7
hamda h(x) funksiyani 2 ta funksiyaning ko‘paytmasi deb qaraymiz:
hʹ(x) = (3cosx ∙log7(x3+2x))ʹ = (3cosx)ʹ·log7(x3+2x) +
cosx 2
![]() cosx ⋅ (log7(x3+2x))ʹ = –3cosx·ln3·sinx·log7(x3+2x)+ 3 3 (3x
+2)
. + 3
cosx ⋅ (log7(x3+2x))ʹ = –3cosx·ln3·sinx·log7(x3+2x)+ 3 3 (3x
+2)
. + 3
(x +2 )x ln7
cosx 2
![]() cosx·ln3·sinx·log7(x3+2x)+ 3
3 (3x
+2)
. ▲
cosx·ln3·sinx·log7(x3+2x)+ 3
3 (3x
+2)
. ▲
Javob: –3
(x +2 )x ln7
1. Murakkab funksiya deb nimaga aytiladi? Misol keltiring.
2. Murakkab funksiyaning aniqlanish sohasi qanday topiladi?
3. Murakkab funksiya hosilasini topish formulasini yoza olasizmi?
4. Murakkab funksiya hosilasini topishni 1–2 ta misolda ko‘rsating.
35. Agar f (x) = x2 −1 bo‘lsa, ko‘rsatilgan funksiyalarni toping:
1 2
1)
f ( ![]() ) ; 2) f (2x); 3) f
(x
−1); 4) f
(x
+1)
−
f
(x
−1).
) ; 2) f (2x); 3) f
(x
−1); 4) f
(x
+1)
−
f
(x
−1).
x
x +1
36. Agar f (x) =
![]() bo‘lsa, ko‘rsatilgan
funksiyalarni toping: x −1
bo‘lsa, ko‘rsatilgan
funksiyalarni toping: x −1
1 1
1)
f ( ![]() ) ; 2) f (
) ; 2) f (
![]() 2 )
; 3) f (x
−1); 4) f
(x
+1) . x x
2 )
; 3) f (x
−1); 4) f
(x
+1) . x x
37. Agar f (x) = x2 , g(x) = x −1 bo‘lsa, quyidagilarni toping:
1) f (g(x)); 2) f ( f (x)); 3) g(g(x)); 4) g( f (x)).
38. Agar f (x) = x3, g(x) = x2 +1 bo‘lsa, quyidagilarni toping: f (x2 )
1)
![]() ; 2)
f
(x)
+
3g(x)
+
3x
−
2
; g(x)−1
; 2)
f
(x)
+
3g(x)
+
3x
−
2
; g(x)−1
3) f (g(x)); 4) g( f (x ).
Tenglikdan foydalanib, f(x) ni toping (39–42):
|
39. f (x +1) = x2 −1. |
1 1
x x |
|
41. f (x +3) = x2 −4. Hosilani toping (43–44): |
1 42*. 2 f (x) +
f
( |
43. 1) f (x) = (3x − 2)5 ; 2) f (x) = esin x ; 3) f (x) = (4−3x)7 ;
![]() 4) f (x)
= sin 2 x
; 5) f
(x)
=
4) f (x)
= sin 2 x
; 5) f
(x)
=
![]() ; 6) f
(x)
=
ln(4x
−1)
; 7) f (x) = 4x
−
5
; 8) f(x)=(2x–1)10; 9) f
(x)
=
cos8 x
.
; 6) f
(x)
=
ln(4x
−1)
; 7) f (x) = 4x
−
5
; 8) f(x)=(2x–1)10; 9) f
(x)
=
cos8 x
.
![]()
![]() 44*. 1) esinx ·tg
44*. 1) esinx ·tg![]() 1 .; 2) 3ctgx·logacosx; 3) lncosx;
1 .; 2) 3ctgx·logacosx; 3) lncosx;
x
4) (x2 – 5x + 4)3 ·10tgx; 5) 7log3x ∙ (x3 – 2x + 1)3; 6) 3cosx·(x2 – 8x + 4)2; 7) ctgx · ln(x2 + x); 8) x2cos30x + 4; 9) 5lnx · ctgx.
 FUNKSIYA
GRAFIGIGA O‘TKAZILGAN 13–14 URINMA VA NORMAL TENGLAMALARI
FUNKSIYA
GRAFIGIGA O‘TKAZILGAN 13–14 URINMA VA NORMAL TENGLAMALARI
Urinma tenglamasi. y = f(x) funksiyaga grafigining (x0; f(x0)) nuqtasidan o‘tuvchi urinma tenglamasini topamiz (19-rasm). Urinma to‘g‘ri chiziq bo‘lgani uchun uning umumiy ko‘rinshi y=kx+b bo‘ladi. Hosilaning geometrik ma’nosiga ko‘ra k =tga= f ′(x0), ya’ni urinma teglamasi y=f ′(x0)x+b ko‘rinishini oladi. Bu urinma (x0; f(x0)) nuqtadan o‘tgani uchun f(x0)=f ′(x0)x0+b bo‘ladi, bundan b=f(x 0)–f ′(x 0)x 0. Topilgan b ni urinma tenglamasiga qo‘yib,
y=f ′ (x0)x+f(x0)–f ′ (x0)x0 yoki
y – f(x0) = f ′(x0)(x – x0) (1)
tenglamani hosil qilamiz.
y – f(x0) = f ′ (x0)(x – x0) tenglama (x0; f(x0)) nuqtada y = f(x) funksiyaga o‘tkazilgan urinma tenglamasi bo‘ladi.
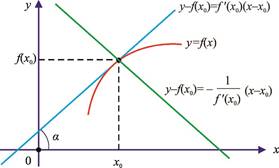
19-rasm.
1-misol. f(x) = x2 – 5x funksiya grafigiga x0=2 abssissali nuqtada o‘tkazilgan urinma tenglamasini yozing.
r Avval funksiyaning va funksiyadan olingan hosilaning x0=2 nuqtadagi qiymatini topamiz:
f (x0) = f(2) = 22 – 5·2 = –6, f ʹ(x) = 2x – 5, f ʹ(2) = 2·2 – 5 = –1.
Topilganlarni (1) tenglamaga qo‘yib, urinma tenglamasini hosil qilamiz:
y − − =− ⋅ −( 6) 1 (x 2) yoki y =− −x 4. Javob: y = – x – 4. ▲
2-misol. f(x)=x 3–2x 2 funksiya grafigiga x0=1 abssissali nuqtada o‘tkazilgan urinma tenglamasini yozing.
r Avval funksiyaning va funksiyadan olingan hosilaning x0=1 nuqtadagi qiymatini topamiz:
f(x0)=f(1)=13–2·12=–1, f ʹ(x)=3x2–4x, f ʹ(1)=3·12–4·1= –1.
Topilganlarni (1) tenglamaga qo‘yib, urinma tenglamasini hosil qilamiz: y–(–1)=–1(x–1) yoki y = –x. Javob: y = –x. ▲
Agar y=f(x) funksiya grafigining x0 abssissali nuqtasida o‘tkazilgan urinma y=kx+b to‘g‘ri chiziqqa parallel bo‘lsa, f '(x0) = k bo‘ladi. Bu shart orqali funksiyaning berilgan to‘g‘ri chiziqqa parallel bo‘lgan urinmasi topiladi.
3-misol. f(x) = x2 – 3x + 4 funksiya uchun y = 2x – 1 to‘g‘ri chiziqqa paral lel bo‘lgan urinma tenglamasini yozing.
r Urinmaning berilgan to‘g‘ri chiziqqa parallellik shartiga ko‘ra,f ′(x0)=2 yoki 2x 0–3=2 tenglam ani hosil qilamiz. Bu tenglamada x0=2,5 bo‘lgani uchun urinma abssissasi x0=2,5 bo‘lgan nuqtadan o‘tadi. Hisoblashlarni bajaramiz: f(x0) = f(2,5) = 2,52 – 3·2,5 + 4 = 6,25 – 7,5 + 4 = 2,75 f ′(x0) = f(2,5) = 2.
Endi urinma tenglamasini topamiz:
y –2,75=2(x–2,5) yoki y=2x–2,25.
Javob: y = 2x – 2,25. ▲
4-misol. f (x)=x3 – 2x2 + 3x – 2 funksiya grafigiga x0= 4 abssissali nuqtada o‘tkazilgan urinma tenglamasini tuzing va urinma bilan Ox o‘qining musbat yo‘nalishi tashkil qilgan burchakning sinusini toping.
r Avval funksiyaning va funksiyadan olingan hosilaning x0 = 4 nuqtadagi qiymatini topamiz:
f(x0)=f(4)=3·43–2·42+3·4–2=170, f ʹ(x)=3x2–4x+3,
f ʹ(4)=3·42–4·4+3= 35.
Topilganlarni (1) tenglamaga qo‘yib, urinma tenglamasini hosil qilamiz: y – 170 = 35(x – 4) yoki y = 35x + 30.
Hosilaning geometrik ma’nosiga ko‘ra tgα=35, bundan

5*-misol. f(x)=x2 parabolaga abssissasi x0 bo‘lgan A nuqtada o‘tka-
zilgan urinma Ox
o‘qini ![]() x0 nuqtada kesib o‘tadi. Shu
da’voni isbotlang.
x0 nuqtada kesib o‘tadi. Shu
da’voni isbotlang.
r f ʹ(x)=2x, f(x0)= x02 , f ʹ(x0)=2x 0.
Urinma tenglamasi (1)
ga ko‘ra y = 2x0 ![]() x– x02 bo‘ladi. Uning Ox o‘qi bilan kesisish nuqtasi x20 ;0 ekani ravshan. Bundan y=x2 parabolaga abssissasi x0 bo‘lgan A nuqtada
o‘tkazilgan urinmani yasash usuli kelib chiqadi: A nuqta va x20 ;0 nuqta orqali o‘tuvchi
to‘g‘ri chiziq y=x2 parabolaga A nuqtada urinadi.
x– x02 bo‘ladi. Uning Ox o‘qi bilan kesisish nuqtasi x20 ;0 ekani ravshan. Bundan y=x2 parabolaga abssissasi x0 bo‘lgan A nuqtada
o‘tkazilgan urinmani yasash usuli kelib chiqadi: A nuqta va x20 ;0 nuqta orqali o‘tuvchi
to‘g‘ri chiziq y=x2 parabolaga A nuqtada urinadi.
|
Normal tenglamasi. y=f (x) funksiya grafigiga x = x0 abssissali nuqtada o‘tkazilgan urinmaga x = x0 nuqtada perpendikular bo‘lgan 1
y – f(x0)=
− f ′(x0) to‘g‘ri chiziqqa y = f(x) funksiya grafigining x0 abssissali nuqtasida o‘tkazilgan normal deyiladi (19- rasm). |
6-misol. f(x) = x5 funksiya grafigiga x0 = 1 abssissali nuqtada o‘tkazilgan normal tenglamasini tuzing.
r Hosila formulasiga ko‘ra f ʹ(x) = 5x4 bo‘ladi. Funksiya va uning hosilasining x0=1 nuqtadagi qiymatlarini hisoblaymiz: f (1)=15=1 va f ′(1) = 5·14 = 5. Bu qiymatlarni normalning tenglamasiga qo‘yamiz va
y−
=−1 ![]() (x−1) yoki y=− +
(x−1) yoki y=− +![]() x tenglamani hosil qilamiz.
x tenglamani hosil qilamiz.
Javob: y = − ![]() x
+ . ▲
x
+ . ▲
|
|
1. y =f(x) funksiya grafigiga x0 abssissali nuqtada o‘tkazilgan urinma tenglamasini yozing.
2. y =f(x) funksiya grafigiga x0 abssissali nuqtada o‘tkazilgan normal tenglamasini yozing.
3. Berilgan funksiyaning biror to‘g‘ri chiziqqa parallel bo‘lganurinmasi qanday topiladi? Misolda tushuntiring.
45.Funksiya grafigiga abssissasi x0=1; x0=–2; x0=0 bo‘lgan nuq- tada o‘tkazilgan urinma tenglamasini yozing:
1)
![]()
![]() f(x)=2x2–5x+1; 2) f(x)=3x–4;
3) f(x)=6;
f(x)=2x2–5x+1; 2) f(x)=3x–4;
3) f(x)=6;
4) f(x)=x3–4x; 5) f(x)=ex; 6) f(x)=2x;
7) f(x)=2x+ln2; 8) f(x)=sinx; 9) f(x)=cosx;
10) f(x)=cosx–sinx; 11) f(x)=exx; 12) f(x)=x·sinx.
46.Funksiya uchun y=7x–1 to‘g‘ri chiziqqa parallel bo‘lgan urinma tenglamasini yozing:
1) f(x)=x3–2x2+6; 2) f(x)=4x2–5x+3; 3) f(x)=8x–4 .
47.Berilgan f(x) va g(x) funksiyalarning urinmalari parallel bo‘ladigan nuqtalarni toping:
1) f x( ) = 3x2 − +5x 4, ,g x( ) = −4x 5;
2) f x( ) = +8x 9, g x( ) =− +5x 8;
3) f x( ) = 7x+11, g x( ) = 7x−9;
4) f x( ) = x3–8, g x( ) = x2+5;
5) f x( ) = +x3 x2, g x( ) = −5x 7;
6) f x( ) = x4+11, g x( ) = x3;+10.
48.Funksiya grafigiga abssissasi a) x0 = 1; b) x0 = –2; d) x0 = 0 bo‘lgan nuqtada o‘tkazilgan normal tenglamasini toping:
1) f(x)=3x2–5x+1; 2) f(x)=3x–40; 3) f (x)=7;
4) f(x)=x3–10x; 5) f(x)=ex; 6) f (x)=12x; 7) f(x)= sinx; 8) f(x)=cosx; 9) f (x)=cosx – sinx; 10) f(x)=eπx; 11) f(x)=x·cosx; 12) f (x)=x ∙ sinx.
1. f (x)=x3+2x2–5x+3 funksiya uchun x0=2 va Δx=0,1 bo‘lganda funksiya orttirmasining argument orttirmasiga nisbatini toping.
2. f (x)=–8x2+4x+1 funksiyaning x0=–3 nuqtadagi hosilasini hisoblang.
3. f (x)=x3–7x2+8x–5 funksiya grafigiga x0= –4 abssissali nuqtada o‘tkazilgan urinma tengl amasini yozing.
4. Moddiy nuqta s(t)=8t2–5t+6 qonuniyat bilan harakatlanmoqda. Agar t – sekund, s – metrlarda o‘lchanadigan bo‘lsa, nuqtaning t0=8 sekunddagi oniy tezligini toping.
5. Ko‘paytmaning hosilasini toping: (3x2–5x+4) · ex. II variant
x2 −5x +6
1.
Bo‘linmaning hosilasini toping: ![]() .
x
+1
.
x
+1
2. Murakkab funksiyaning hosilasini toping: ctg15x.
3.
f x( ) = ![]() x funksiyaning x0
=
x funksiyaning x0
=
![]() nuqtadagi hosilasini
hisoblang.
nuqtadagi hosilasini
hisoblang.
4. f x( ) = ln(x +1) funksiya grafigiga x=0 nuqtada o‘tkasilgan urinma tenglamasini yozing.
5. s t( ) = 0,5t2 − 6t +1 qonuniyati bilan harakatlanayotgan moddiy nuqtaning t=16 sekunddagi oniy tezligini toping. (t – sekundda, s – metrlarda o‘lchanadi).

49. y=f(x) funksiya uchun x0 va x nuqtalarga mos h va Δy ni hisoblang:
1) f(x)=4x2–3x+2, x0=1, x=1,01; ![]() 2) f(x)=(x+1)3, x0=0, x=0,1.
2) f(x)=(x+1)3, x0=0, x=0,1.
50. Agar x0 = 3 va Δx = 0,03 bo‘lsa, berilgan funksiyalar uchun: a) funksiya orttirmasini; b) funksiya orttirmasining argument orttirmasiga nisbatini toping:
1) f (x)=7x – 5; 2)
f(x)=2x2–3x; ![]() 3) f(x)=x3+2;
3) f(x)=x3+2; ![]() 4) f(x)=x3+4x.
4) f(x)=x3+4x.
51. Agar x0=2 va Δx=0,01 bo‘lsa, berilgan funksiyalar uchun: a) funks iya orttirmasini; b) funksiya orttirmasining argument orttirmasiga nisbatini toping:
1) f(x)=– 4x+3;
![]() 2) f(x)=–8;
2) f(x)=–8;
![]() 3) f(x)=x2+10x;
3) f(x)=x2+10x; ![]() 4)
f(x)=x3–10.
4)
f(x)=x3–10.
52. x→0 bo‘lsa, funksiya qaysi songa intiladi:
1) f(x)=x 3–2x 2+3x+4; 2) f(x)=x5–6x4+8x–7;
3) f(x)=(x2–5x+1)(x3–7x2–11x+6);
x2 − x −19 x3 −8x
|
x +7x −28 53. Funksiyaning hosilasini toping: |
x3 + x2 + x +1 |
|
1) y=17x; 2) y=29x–3; |
3) y=–15; 4) y=16x2–3x; |
|
5) y=–5x+40; 6) y=18x–x2; |
7) y=x2+15x; |
|
8) y=16x3+5x2–2x+14; |
9) y=3x3+2x2+x. |
4) f(x)= ![]() 2 ; 5) f(x)=
2 ; 5) f(x)= ![]() ?
?
54. Funksiyaning hosilasini: a) x = –3; b) x = 1,1; c) x = 0,4; d) x = – 0,2 nuqtalarda hisoblang:
1) y = 1 5 x ; 2) y=9x+3;
3) y=–20; 4) y=5x 2+x; 5) y=–8x+4; 6) y=8x–x2; 7) y=x2+25x; ![]() 8) y=x3+5x2–2x+4.
8) y=x3+5x2–2x+4.
55. y=f(x) funksiya hosilasini ta‘rifga ko‘ra toping:
1) f
(x)=
2x2 +3x
+5; 3*) f (x)=
![]() x +1
;
x +1
;
x
2) f
(x)=
(x
+
2)3; 4*) f x( )=
![]() x2
+1. x
x2
+1. x
56. ![]() y= f (x) funksiyaning x0 nuqtadagi hosilasini toping: 1) f(x)=4x3+3x2+2x+1, x0=1; 2) f x( ) =x3
+sin22
,°
x0=–1;
y= f (x) funksiyaning x0 nuqtadagi hosilasini toping: 1) f(x)=4x3+3x2+2x+1, x0=1; 2) f x( ) =x3
+sin22
,°
x0=–1;
3
x −1
![]() 3) f x( ) =(2x+1)(
x
−1), x0=4; 4) f x(
) =
3) f x( ) =(2x+1)(
x
−1), x0=4; 4) f x(
) = ![]() x2+1, x0=–3.
x2+1, x0=–3.
57. Moddiy nuqta s(t) =
![]() t3
−t
+
5 qonuniyat bilan harakatlanmoqda
t3
−t
+
5 qonuniyat bilan harakatlanmoqda
(s metrda, t – sekundda). Moddiy nuqtaning 2-sekunddagi tezligini toping.
58. Funksiyaning hosilasini toping:
|
1) y = |
x ; |
|
|
|
![]()
![]() x; 4) y
=
(2x
+
3)3; 5*) y = x·lnx·(x+1); 6) y
=
(x
+
x)(
x
−
2); x + 2
x; 4) y
=
(2x
+
3)3; 5*) y = x·lnx·(x+1); 6) y
=
(x
+
x)(
x
−
2); x + 2
7) y
=
![]() ;
8) y=10 x+log 25+cos15°; sin x
;
8) y=10 x+log 25+cos15°; sin x
9) y = 3−x ⋅sin x ; 10*) y=tgx·cosx+7x·x7;
11) f
(x)=
![]() x4
−8x2
+
3; 12) f (x)
=
x4
−8x2
+
3; 12) f (x)
=
![]() x
−
sin
x + 5 ;
x
−
sin
x + 5 ;
10 2x
13) f x( ) =
x −80x
; 14) f
x(
) =
8x
− ![]() .
.
ln2
59. Funksiya hosilasining x0 nuqtadagi qiymatini hisoblang:
1) f
(x)
= ![]() 1 , x0 = 0; 2) f(x)=(x2+3x)lnx,
x0=1;
cos
x
1 , x0 = 0; 2) f(x)=(x2+3x)lnx,
x0=1;
cos
x
![]() arctg2x x(x–ln2), x0=ln2.
arctg2x x(x–ln2), x0=ln2.
3) f x( ) = , x0 = 1; 4) f(x)=e 1+ x
60*. f '(x) > 0 tengsizlikni yeching:
1) f(x) = x·ln27–3x; 2) f (x) = sin x − 2x ;
1 3 3 2
61. ![]() Moddiy
nuqta s(t) =
t
−
t
+
2t qonuniyat bilan harakatlanmoqda.
Moddiy
nuqta s(t) =
t
−
t
+
2t qonuniyat bilan harakatlanmoqda.
3 2
Moddiy nuqtaning tezligi qachon nolga teng bo‘ladi? Buning ma’nosi nima?
![]()
![]() 5 414 5
5 414 5
62. ![]() Hosilani
toping: 1) y= x − x
+
x
; 2) y=
Hosilani
toping: 1) y= x − x
+
x
; 2) y= ![]() 2
−
x; 3) y= x +
x
. x
2
−
x; 3) y= x +
x
. x
63. Moddiy nuqtaning t0 vaqtdagi tezligini toping:
![]()
![]() 1) x(t)
=t4
−
2t3
+t
, t0 =−5; 2) x(t) =−5t
+t
2 −t
, t0= 4.
1) x(t)
=t4
−
2t3
+t
, t0 =−5; 2) x(t) =−5t
+t
2 −t
, t0= 4.
Hosilani toping (64–66):
![]()
![]() 2–5x); 2) y =
x2 −3x
; 3) y
=
(x4
+
x)(x3
−5
)x ;
2–5x); 2) y =
x2 −3x
; 3) y
=
(x4
+
x)(x3
−5
)x ;
64. 1) y = (x+2)(x
![]() 3+4x2+5x; 5) y
=
−14 x
; 6) y = 7x2
+12x
+
2019
.
3+4x2+5x; 5) y
=
−14 x
; 6) y = 7x2
+12x
+
2019
.
4) y = 2x
x 14
![]()
![]() 10x8 x3 +5 x
+1 10+x–10)(x8+x–8).
10x8 x3 +5 x
+1 10+x–10)(x8+x–8).
65*. 1) y = xx10 −1; 2) y = x + 7 ; 3) y=(x
66*. 1) y = 3x ⋅sin x ; 2) y = e5x(cos x −sin x); cos x
ln x
3)
y=xctgx; 4) y=
![]() 2 . x
2 . x
67*. Hosilani x0 nuqtada hisoblang:
1) f
x(
) =![]() , x0 = –2; 2) f(x)=ctgx–2x+2,
x0
=
, x0 = –2; 2) f(x)=ctgx–2x+2,
x0
=
![]() ;
;
3) f
(x)
=
x2(lg
x −1), x0 =1; 4) ( )f x =
ctgx
−
![]() ln x , x0=1.
ln x , x0=1.
68*. Murakkab funksiyaning hosilasini toping:
1) x2·sinx; 2) log15cosx; 3) lnctgx;
4) tg35x; 5) ectgx; 6) 23cosx;
7) 35sinx; 8) (x2–10x+7)lncosx;
9) ![]() x5 −6xx
+
4
; 10) e–3x(x4–3x2+2); 11) lntgx; e
x5 −6xx
+
4
; 10) e–3x(x4–3x2+2); 11) lntgx; e
12) x3 + +7 1x ; 13) e5x(x5+8x+11); 14) lncos2x.
e2x
HOSILA YORDAMIDA FUNKSIYANI
18–21
![]() TEKSHIRISH
VA GRAFIKLARNI YASASH
TEKSHIRISH
VA GRAFIKLARNI YASASH
Funksiyaning o‘sishi va kamayishi. O‘suvchi va kamayuvchi funksiyalar bilan tanishsiz. Endi funksiyaning o‘sish va kamayish oraliqlarini aniqlash uchun hosila tushunchasidan foydalanamiz.
1-teorema. y = f(x) funksiya (a; b) oraliqda aniqlangan va hosilasi mavjud bo‘lsin. Agar x∈(a; b) uchun f ′(x) > 0 bo‘lsa, y = f(x) funksiya (a; b) oral iqda o‘suvchi funksiya bo‘ladi (20-rasm).
2-teorema. y = f(x) funksiya (a; b) oraliqda aniqlangan va hosilasi mavjud bo‘lsin. Agar x∈ (a; b) uchun f ′(x) < 0 bo‘lsa, y = f(x) funksiya (a; b) oraliqda kamayuvchi funksiya bo‘ladi (21-rasm).
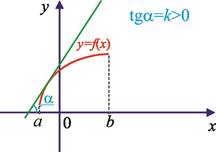
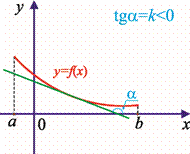
20-rasm. 21-rasm.
1, 2- teoremalarni isbotsiz qabul qilamiz.
1-misol. Funksiyaning o‘sish va kamayish oraliqlarini toping:
f x( ) = 2x3 − 3x2 −12x + 3 .
r Bu funksiya (−∞ +∞; ) oraliqda aniqlangan. Uning hosilasi:
f '(x) = 6x2 − 6x −12 = 6(x − 2)(x +1) .
f '(x) > 0 , f '(x) < 0 tengsizliklarni oraliqlar usuli bilan yechib, (−∞;−1)
va (2;+∞) oraliqlarda funksiyaning o‘sishi hamda (–1;2) oraliqda funksiyaning kamayishini bilib olamiz.
Javob: (–∞; –1) va (2; +∞) oraliqlarida funksiya o‘sadi; (–1; 2) oraliqda esa funksiya kamayadi. ▲
2-misol. Funksiyaning o‘sish va
kamayish oraliqlarini toping: 1 . f (x)
=
x
+
![]()
x
r Bu funksiya (−∞;0) ∪ (0;+∞) oraliqda aniqlangan. Uning hosilasi:
![]() 1
1
f '(x)
=1− ; f ʹ(x) > 0, ya’ni 1− ![]() 2
>
0 tengsizlikni oraliqlar usuli bilan x x
2
>
0 tengsizlikni oraliqlar usuli bilan x x
yechib, hosilaning (–∞; –1) va (1; +∞) oraliqlarda musbatligini topamiz.
1
Xuddi
shuningdek, f '(x) <
0
, ya‘ni 1− ![]() 2
<
0 tengsizlikni oraliqlar usuli x
2
<
0 tengsizlikni oraliqlar usuli x
bilan yechib, bu tengsizlik (–1; 0) va (0; 1) oraliqlarda bajarilishini bilib olamiz.
Javob: funksiya (–∞; –1) va (1; +∞) oraliqlarda o‘sadi; funksiya (–1; 0) va (0; 1) oraliqlarda esa kamayadi. ▲
Funksiyaning statsionar nuqtalari. y = f (x) funksiya (a; b) oraliqda aniqlangan bo‘lsin.
1-ta’rif. y = f(x) funksiyaning hosilasi 0 ga teng bo‘ladigan nuqtalar statsionar nuqtalar deyiladi.
3-misol. Funksiyaning statsionar nuqtalarini toping: f x( ) 2= x3−3x2−12x+3.
r Funksiyaning hosilasini topib, uni nolga tenglaymiz: f ʹ(x) = 6x2– – 6x – 12 = 0. Bu tenglamani yechib funksiyaning statsionar nuqtalari x1= –1 , x2=2 ekanini topamiz.
Javob: funksiyaning statsionar nuqtalari x1 = –1, x2 = 2. ▲
Funksiyaning lokal maksimum va lokal minimumlari. Funksiyaning lokal maksimum va lokal minimumlarini aniqlash uchun hosiladan foyda- lanamiz.
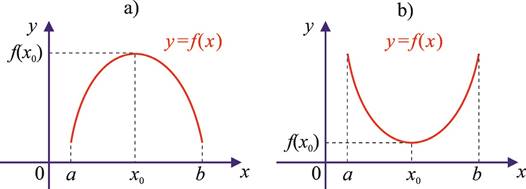
22- rasm.
3-teorema. f (x) funksiya (a; b) oraliqda aniqlangan va f ′(x) mavjud; (a; x0) oraliqda f '(x) > 0 va (x0; b)oraliqda f '(x) < 0 bo‘lsin, x0∈(a; b). U holda x0 nuqta f (x)funksiyaning lokal maksimumi bo‘ladi (22-a rasm). 4-teorema. f (x) funksiya (a; b)oraliqda aniqlangan va f ′(x) mavjud; (a;x0) oraliqda f '(x) < 0 va (x0;b) oraliqda f '(x) > 0 bo‘lsin, x0∈(a, b).
U holda x0 nuqta f (x)funksiyaning lokal minimumi bo‘ladi (22-b rasm).
3, 4-teoremalarni isbotsiz qabul qilamiz.
2-ta‘rif. Funksiyaning lokal maksimum va lokal minimumlariga uning ekstremumlari deyiladi.
4-misol. Funksiyaning lokal maksimum va lokal minimum nuqtalarini toping: f (x)= x3 −3x+3.
r Funksiyaning hosilasini topamiz: f ′(x)= 3x2 −3 = 3(x−1)(x+1). Hosila barcha nuqtalarda aniqlangan va x =±1 nuqtalarda nolga aylanadi. Shuning uchun x =±1 nuqtalar funksiyaning kritik nuqtalaridir. Oraliqlar usulidan foydalanib (–∞; –1) va (1; +∞) oraliqlarda f '(x) > 0 , (–1; 1) oraliqda esa f '(x) < 0 ekanini aniqlaymiz. Demak, x =−1 lokal maksimum va x =1 lokal minimum nuqtalari ekan (23-rasm).
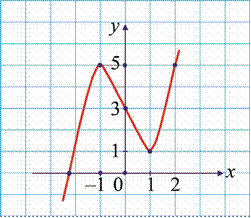
23-rasm.
Javob: x =−1 lokal maksimum va x =1 lokal minimum nuqta. ▲
Funksiyaning eng katta va eng kichik qiymatlari bilan 10-sinfdan tanishmiz.
f(x) funksiya [a; b] kesmada aniqlangan va (a; b) da hosilasi mavjud
bo‘lsin. Uning eng katta qiymatini topish qoidasi shunday:
1) funksiyaning bu oraliqdagi barcha statsionar nuqtalari topiladi;
2) funksiyaning statsionar, chegaraviy a va b nuqtalardagi qiymatlari hisoblanadi;
3) bu qiymatlarning eng kattasi funksiyaning shu oraliqdagi engkatta qiymati deyiladi.
Funksiyaning eng kichik qiymati ham shu kabi topiladi.
5-misol. f (x)= x3 + 4,5x2 – 9 funksiyaning [–4; 2] oraliqdagi eng katta va eng kichik qiymatl arini toping.
r Funksiyaning hosilasini topamiz: f ′(x)=3x2+9x. Hosilani nolga teng lab, funksiyaning statsionar nuqtalarini topamiz: f ′(x)=3x(x+3)=0, x 1= 0 va x 2= –3. Funksiyaning topilgan x1= 0, x2= –3 hamda a= –4, b=2 nuqtalardagi qiymatlarini topamiz:
f(0)=03+4,5∙02–9=–9, f(–3)=(3)3+4,5∙(–3)2–9=4,5, f(–4)=(–4)3+4,5∙42–9=–1, f(2)=23+4,5 ∙22–9=17.
Demak, funksiyaning eng katta qiymati 17 va eng kichik qiymati –9 ekan. Javob: funksiyaning eng katta qiymati 17 va eng kichik qiymati –9. ▲
Hosila yordamida funksiyani tekshirish va grafigini yasash. Funksiya grafigini yasashni quyidagi ketma-ketlikda amalga oshiramiz.
Funksiyaning:
1) aniqlanish sohasini;
2) statsionar nuqtalarini;
3) o‘sish va kamayish oraliqlarini;
4) lokal maksimum va lokal minimumlarini hamda funksiyaning shu nuqtalardagi qiymatlarini topamiz;
5) topilgan ma’lumotlarga ko‘ra funksiyaning grafigini yasaymiz.
Grafikni yasashda funksiya grafigini koordinata o‘qlari bilan kesisish va boshqa ayrim nuqtalarini topish maqsadga muvofiq.
6-misol. f(x)=x 3–3x funksiyani hosila yordamida tekshiring va uning grafigini yasang.
1. Funksiya (–∞; +∞) oraliqda aniqlangan.
2. Statsionar nuqtalarini topamiz:
f ′(x)=(x3–3x)′ = 3x2–3=0. x1=1 va x2= –1 statsionar nuqtalardir.
3. Funksiyaning o‘sish va kamayish oraliqlarini topamiz:
(–∞; –1) U (1; +∞) oraliqlarda f ′(x) > 0 bo‘lgani uchun f (x) funksiya shu oraliqlarda o‘sadi va (–1; 1) oraliqda f ′(x) < 0 bo‘lgani uchun f(x)=x 3–3x funksiya (–1; 1) oraliqda kamayadi.
4. x=–1 bo‘lganda funksiya lokal maksimum f (–1)=(–1)3–3∙(–1) = 2 ga va x=1 bo‘lganda funksiya lokal minimum f (1)=13–3∙1=–2 ga ega.
5. ![]()
![]() Funksiyaning
Ox o‘qi bilan kesisish
nuqtalarini topamiz: x 3–3x=x(x 2–3)=0. Bundan x=0 yoki x2–3=0 tenglamani hosil
qilamiz. Tenglamani yechib x1= 0, x2 = 3 , x3 = – 3 funksiya
grafigining Ox o‘qi bilan kesisish nuqtalarini topamiz. Natijada 24- rasmdagi
grafikni hosil qilamiz.
Funksiyaning
Ox o‘qi bilan kesisish
nuqtalarini topamiz: x 3–3x=x(x 2–3)=0. Bundan x=0 yoki x2–3=0 tenglamani hosil
qilamiz. Tenglamani yechib x1= 0, x2 = 3 , x3 = – 3 funksiya
grafigining Ox o‘qi bilan kesisish nuqtalarini topamiz. Natijada 24- rasmdagi
grafikni hosil qilamiz.
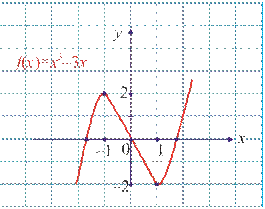
24-rasm.
1. Funksiyaning o‘sish va kamayish oraliqlari qanday topiladi?
2. Funksiyaning statsionar nuqtasiga ta‘rif bering.
3. Funksiyaning lokal maksimum va lokal minimumlari qandaytopiladi?
4. Funksiyaning eng katta va eng kichik qiymatlari qanday topiladi?
5. Hosila yordamida funksiyaning grafigini yasash bosqichlarini ayting va bitta misolda tushuntiring.
6. Funksiyaning statsionar nuqtalari uning ekstremum nuqtalari bo‘lishi shartmi? Misollar keltiring.
1 4 1 2
7.
![]() f
x(
) = x
− x funksiyani hosila yordamida tekshiring va grafigini
f
x(
) = x
− x funksiyani hosila yordamida tekshiring va grafigini
4 2
yasang.
69. Funksiyaning o‘sish va kamayish oraliqlarini toping:
1) f
(x)=
2
−
9x
; 2) f
(x)=
![]() x −8; 3) f
x(
)=
−x3
27x
;
x −8; 3) f
x(
)=
−x3
27x
;
![]() 4) f (x)=
4) f (x)=
![]() x −1
; 5) f (x)
=
x2 −2x+
4; 6) f (x)=
x(x2 −6); x
x −1
; 5) f (x)
=
x2 −2x+
4; 6) f (x)=
x(x2 −6); x
7) f
(x)=−x2 +
2x−3; 8) f (x)=
![]() 12
; 9) f (x)=
x4 −2x2 ; x
12
; 9) f (x)=
x4 −2x2 ; x
10) f x( )=
3x4−8x3+16; ![]() 11) f
(x)=
11) f
(x)= ![]() 1
2 ; 12)
f
(x)=
sin
x ;
1
2 ; 12)
f
(x)=
sin
x ;
1+ x
13) f (x) = cos x; 14) f(x)=tgx; 15*) f (x)= sin 2x + cos2x .
70. Funksiyaning statsionar nuqtalarini toping:
1 3
1) ![]() f (x)=
2x2 −3x+1;
f (x)=
2x2 −3x+1; ![]() 2) f
(x)=
9x −
2) f
(x)=
9x − ![]() 3
x ; 3*) f
(x)=
x
−1
;
3
x ; 3*) f
(x)=
x
−1
;
![]() 4) f
(x)=
x2; 5) f (x)=8x3 +5x
; 6) f (x)=
3x
−
4
; 7*) f (x)=
x
+1; 8) f (x)=
2x3 +3x2 −6; 9) f (x)=
3+8x2 −
x4 .
4) f
(x)=
x2; 5) f (x)=8x3 +5x
; 6) f (x)=
3x
−
4
; 7*) f (x)=
x
+1; 8) f (x)=
2x3 +3x2 −6; 9) f (x)=
3+8x2 −
x4 .
71. Funksiyaning lokal maksimum va lokal minimumlarini toping:
1) f (x)= x2 − x4; 2) f (x)=(x−4)8 ; 3) f (x)= 4−3x2 −2x3;
![]()
![]() 4) f
(x)=
5 + x
; 5) f
(x)=
x4 −2x3 +
x2 −3; 6) f(x)=3tgx; x
5
4) f
(x)=
5 + x
; 5) f
(x)=
x4 −2x3 +
x2 −3; 6) f(x)=3tgx; x
5
7) f (x) = 2sinx + 3; 8) f (x) = –5cosx–7; 9) f(x)=x 4–x 3+4.
72. Funksiyaning o‘sish va kamayish oraliqlarini toping:
1) f
x(
)=
−x3
27x
; 2*) f (x)= ![]() 23x
; 3*) f (x)=
x
+
23x
; 3*) f (x)=
x
+
![]() 42
;
42
;
x +1 x
4) f (x)=5sinx+13; 5) f (x)=15cosx–7; 6) f (x)= –3tgx.
73. Funksiyaning eng katta va eng kichik qiymatlarini toping:
1) f
(x)=
x4 −8x2 +3, x∈[−
4;
1]; ![]() 2) f
(x)=
3x5 −5x3 +1, x∈ [− 2;
2];
2) f
(x)=
3x5 −5x3 +1, x∈ [− 2;
2];
![]() 3) f (x)=
3) f (x)=
![]() x , x∈[1;
2]; 4) f (x)=
3x3 −6x2 −5x+8, x∈ [−1;
4].
x , x∈[1;
2]; 4) f (x)=
3x3 −6x2 −5x+8, x∈ [−1;
4].
x +1
74. Funksiyani tekshiring va grafigini yasang:
1) ![]() y =
x3 −
6x2 +
9x
−
2; 2) y =
y =
x3 −
6x2 +
9x
−
2; 2) y = ![]() x5
−
x5
−
![]() x3
+1;
x3
+1; ![]() 3) y
=
x4
−
4x3
+15
.
3) y
=
x4
−
4x3
+15
.
75*. Funksiya hosilasining grafigiga qarab (25, 26-rasmlar), quyidag ilarni toping:
|
1) statsionar nuqtalarni; |
2) o‘sish oraliqlarini; |
|
3) kamayish oraliqlarini; 5) lokal minimumlarni. |
4) lokal maksimumlarini; |
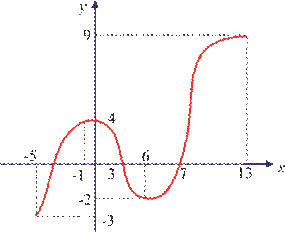
25-rasm.
26-rasm.
1. Hosilani toping: f (x) = 20x3 + 6x2 – 7x + 3.
![]() 2 – 5x + 4 va g
x(
)= x+1 bo‘lsa, f(g(3)) ni hisoblang.
2 – 5x + 4 va g
x(
)= x+1 bo‘lsa, f(g(3)) ni hisoblang.
2. f (x) = x
x−2
3. f (x)= −x3 5x2+ +7x 1 funksiya uchun quyidagilarni toping:
1) statsionar nuqtalarni;
2) o‘sish oraliqlarini;
3) kamayish oraliqlarini;
4) lokal maksimumlarini;5) lokal minimumlarini.
4. Hosilani toping: (3x + 5)3 + sin2x.
1
5. ![]() f x(
) = 1−3x bo‘lsa f '
f x(
) = 1−3x bo‘lsa f ' ![]() ni hisoblang.
ni hisoblang.
4
1. Hosilani toping: f (x) = 10x3+16x2+7x–3.
![]() 2+6x–3 va g
x(
) =
x
−1 bo‘lsa, f(g(3)) ni hisoblang.
2+6x–3 va g
x(
) =
x
−1 bo‘lsa, f(g(3)) ni hisoblang.
2. f (x) =x
x + 2
3. f (x) =x3+2x2–x+3 funksiya uchun quyidagilarni toping:
1) statsionar nuqtalarni;
2) o‘sish oraliqlarini;
3) kamayish oraliqlarini;
4) lokal maksimumlarini;5) lokal minimumlarini.
4. Hosilani toping: (2x – 6)3 + cos2x.
3
5.
![]() f
x(
) = 1−
2x bo‘lsa, f
'
f
x(
) = 1−
2x bo‘lsa, f
' ![]() ni hisoblang.
ni hisoblang.
8
![]() GEOMETRIK,
FIZIK, IQTISODIY MAZMUNLI 22–25 EKSTREMAL MASALALARNI YECHISHDA DIFFERENSIAL HISOB USULLARI
GEOMETRIK,
FIZIK, IQTISODIY MAZMUNLI 22–25 EKSTREMAL MASALALARNI YECHISHDA DIFFERENSIAL HISOB USULLARI
1-masala. To‘g‘ri to‘rtburchak shaklidagi yer maydoni atrofini 100 m panjara bilan o‘rashmoqchi. Bu panjara eng ko‘pi bilan necha kvadrat mert yer maydonini o‘rashga yetadi?
r Yer maydonining eni x m va bo‘yi y m bo‘lsin (27-rasm).
Masala shartiga ko‘ra yer maydoni-
![]() ning perimetri 2x +2y=100. Bundan
ning perimetri 2x +2y=100. Bundan
y = 50–x. Yer maydonining yuzi S(x) = xy =x(50–x)=50x–x 2. Ma- x m sala S(x) funksiyaning eng katta qiy- matini topishga keltirildi. Avval S(x)
funksiyaning statsionar nuqtasini to- y m pamiz: Sʹ(x)=50–2x=0, bundan x = 25. 27-rasm.
(–; 25) oraliqda Sʹ(x) > 0 va
(25; +) oraliqda Sʹ(x) < 0 bo‘lgani uchun S(x) funksiya x=25 da eng katta qiymatga ega bo‘ladi va S(25)=625. Demak, 100 m panjara yordamida eng ko‘pi bilan 625 m2 yer maydonini o‘rash mumkin. Javob: 625 m2. ▲
Umuman, perimetri berilgan barcha to‘g‘ri to‘rtburchaklar ichida yuzasi eng kattasi kvadratdir.
![]() 2-masala. Tomoni a cm
bo‘lgan kvadrat shaklidagi kartondan usti ochiq quti tayyorlashmoqchi. Bunda
kartonning uchlaridan bir xil kvadratchalar kesib olinadi. Qutining hajmi eng
katta bo‘lishi uchun uning asos tomoni uzunligi necha santimetr bo‘lishi kerak?
2-masala. Tomoni a cm
bo‘lgan kvadrat shaklidagi kartondan usti ochiq quti tayyorlashmoqchi. Bunda
kartonning uchlaridan bir xil kvadratchalar kesib olinadi. Qutining hajmi eng
katta bo‘lishi uchun uning asos tomoni uzunligi necha santimetr bo‘lishi kerak?
r Kartonning uchlaridan bir xil kvadr atchalar qirqib olinib, asosi x cm bo‘lgan ochiq quti yasal gan, desak (28-rasm), kesib olingan kvadrat-
a −
x
cha ning to moni ![]() cm bo‘ladi. Shuning
uchun
cm bo‘ladi. Shuning
uchun
2
a x−
ochiq qutining hajmi ![]() 28-rasm.
28-rasm.
![]() x3 ax2 x3 ax2
x3 ax2 x3 ax2
=
− + cm3. Demak, berilgan masala V x(
)=−
+ ![]() funk siyaning
funk siyaning
2 2 2 2
[0; a] kesmadagi
eng katta qiymatini topishga keldi. V(x) funksiyaning statsionar
nuqtalarini topamiz: V x′(
) =
− ![]() x2
+
ax
=
0.
x2
+
ax
=
0.
Bu yerdan x1 =
0
, x2 =
![]() a statsionar nuqtalar topiladi. Ravshanki,
a statsionar nuqtalar topiladi. Ravshanki,
![]()
![]()
2
2 3
2 (x) ning [0; a]
2
2 3
2 (x) ning [0; a]
V a= a va V a >V(0)=V(a)= 0 . Demak, V
3 27 3
kesmadagi eng katta
qiymati ![]() a3 bo‘ladi.
a3 bo‘ladi.
Javob: ochiq qutining asos tomoni uzunligi x
=
![]() a cm. ▲
a cm. ▲
4
t 3
3-masala. Moddiy nuqta s
t(
) =
− ![]() +t qonuniyat bilan harakatlanmoq-
+t qonuniyat bilan harakatlanmoq-
12
da (s(t) metrda, t vaqt esa sekundda o‘lchanadi). Quyidagilarni toping:
1) Eng katta tezlanishga erishiladigan vaqtni (t0);
2) t0 vaqtdagi oniy tezlikni;
3) t0 vaqt ichida bosib o‘tilgan yo‘lni toping. r Moddiy nuqtaning tezligini topamiz:
'
![]()
![]() v
t(
) =
s
t
v
t(
) =
s
t
′( ) = − 12t4 +t3 = − t33 +3t2 .
Fizikadan ma’lumki, tezlikdan olingan hosila tezlanishni beradi, ya’ni:
a(t) = vʹ (t) = – t2 + 6t.
1) Eng katta tezlanishga ega bo‘ladigan t0 vaqtni aniqlash uchun a(t)=vʹ (t)= –t2+6t funksiyani maksimumga tekshiramiz. Avval aʹ (t) = –2t + 6 = 0 tenglamani yechamiz, bundan t0 = 3. (0; 3) oraliqda aʹ (t) > 0 va (3;+∞) oraliqda aʹ(t) < 0 bo‘lgani uchun t=3 da a(t) eng katta qiymatga erishadi.
2)
t0
vaqtdagi oniy tezlikni hisoblaymiz: v![]() .
.
t4 3
3)
t0 vaqt ichida bosib o‘tilgan yo‘l s
t(
) =
− ![]() +t formulaga t0=3 ni
+t formulaga t0=3 ni
12
34 3 27 81
qo‘yib hisoblanadi: s(3)
=
− ![]() +3 =
−
+3 =
− ![]() + 27
=
+ 27
= ![]() = 20,25
m.
= 20,25
m.
12 4 4 m
Javob: 1) 3 s; 2) 18 ![]() ; 3) 20,25 m. ▲ s 3
; 3) 20,25 m. ▲ s 3
4-masala. Moddiy nuqta s
t(
) =
![]() t −t2
+
4t
+50 qonuniyat bilan harakat-
t −t2
+
4t
+50 qonuniyat bilan harakat-
3
lan moqda (s(t) masofa metrda, vaqt t sekundda o‘lchanadi). Quyidagilarni toping:
1) eng kichik tezlikka erishiladigan vaqtni (t0);
2) t0 vaqtdagi tezlanishni;
3) t0 vaqt ichida bosib o‘tilgan yo‘lni.
r Moddiy nuqtaning tezligi va tezlanishini topamiz:
![]()
t 2 v
t(
) =
s
t
t 2 v
t(
) =
s
t
′( ) = 33 −t + 4t +50' = t2 −2t + 4,
2 ' a t( ) = v t′( ) = (t −2t + 4) = 2t −2.
1) Eng kichik tezlikga erishiladigan t0 vaqtni aniqlaymiz: vʹ (t) = (t2–2t + 4)ʹ = 2t–2 = 0, bundan t0=1.
(0; 1) oraliqda v' (t) < 0 va (1; + ) oraliqda v' (t) > 0 bo‘lgani uchun t0=1 da v (t) eng kichik qiymatga erishadi.
2) t0 vaqtdagi tezlanishni hisoblaymiz: a(1) = 2∙1–2 = 0 m/s2.
t3 2
3) t0 vaqt ichida bosib o‘tilgan yo‘lni s
t(
) = ![]() −t + 4t
+50 formulaga 3
−t + 4t
+50 formulaga 3
t0=1 ni qo‘yib hisoblanadi,
ya‘ni s ![]() 1 1 4
1 50 53 m.
1 1 4
1 50 53 m.
Javob: 1) 1 s; 2) 0 m/s2; 3) 53![]() m. ▲
m. ▲
5-masala. Havo shariga t ∈ [0; 8] minut oralig‘ida V(t) = 2t3–3t2+10t+2 (m3) hajmda havo purkalmoqda. Quyidagilarni toping:
1) boshlang‘ich vaqtdagi havo hajmini;
2) t = 8 minutdagi havo hajmini;
3) t = 4 minutdagi havo purkash tezligini;
r 1) boshlang‘ich vaqtdagi havo hajmini topish uchun V(t)=2t3– –3t2+10t+2 m3 formulaga t = 0 qo‘yiladi, ya‘ni V(0) = 2 m3.
2) t = 8 minut vaqtdagi havo hajmini topish uchun V(t)=2t3–3t2+10t+2 m3 for mulaga t = 8 qo‘yiladi:
V(8) = 2 ∙ 83–3∙82+10 ∙ 8+2 = 1024–192+80+2 = 914 m3; 3) havo purkash tezligini topamiz:
![]() ′(
) =
(2t3
−3t2
+10t
+
2)'
=
6t2 −6t
+10
min.m3
. v v
t
′(
) =
(2t3
−3t2
+10t
+
2)'
=
6t2 −6t
+10
min.m3
. v v
t
Demak, v′(4)
=
6
4⋅
2
−6
4⋅ +10
=
96−24+10
=
82
![]() minm3
.
minm3
.
m3
Demak, a(3)=12
3⋅
−6
=
30
![]() min2
.
min2
.
m3
Javob: 1) 2 m3; 2) 914 m3; 3) 82 ![]() . ▲ min
. ▲ min
6-masala. Karima ko‘ylak tikish uchun buyurtma oldi. Bir oyda x ta ko‘ylak tiksa, p(x) = –x2 +100x ming so‘m daromad qiladi. Quyidagilarni toping:
1) eng katta daromad olish uchun qancha ko‘ylak tikish kerak?
2) eng katta daromad qancha bo‘ladi?
r 1) p(x)= – x2+100x funksiyani maksimumga tekshiramiz:
p'(x) = −( x2 +100 )x ' = −2x +100 = 0, bundan x0=50. (0; 50) kesmada pʹ(x)>0 va (50; +) oraliqda pʹ(x) < 0 bo‘lgani uchun x0=50 bo‘lganda funksiya eng katta qiymatga ega bo‘ladi. Demak, eng katta daromad olish uchun 50 ta ko‘ylak tikish kerak ekan.
2) Eng katta daromad qanchaligini topish uchun p(x) = – x2+100x ifodaga x0=50 ni qo‘yamiz:
p(50)=–502+100·50=–2500+5000=2500(ming so‘m)=2500000 so‘m.
Javob: 1) 50 ta ko‘ylak; 2) 2 500 000 so‘m. ▲
Hosilani tatbiq qilib yechiladigan:
1) geometrik; 2) fizik; 3) iqtisodiy mazmunli masalaga misol keltiring.
76.To‘g‘ri to‘rtburchak shaklidagi yer maydonining atrofini o‘rashmoqchi. 300 m panjara yordamida eng ko‘pi bilan necha kvadrat metr yer maydonini o‘rash mumkin?
77.To‘g‘ri to‘rtburchak shaklidagi yer maydonining atrofini o‘rashm oqchi. 480 m panjara yordamida eng ko‘pi bilan necha kvadrat metr yer maydonini o‘rash mumkin?
78*. Tomoni 120 cm bo‘lgan kvadrat shaklidagi kartondan usti ochiq quti tayyorlandi. Bunda kartonning uchlaridan bir xil kvadratchalar kesib olindi. Qutining hajmi eng katta bo‘lishi uchun kesib olingan kvadratchaning tomoni necha santimetr bo‘lishi kerak?
79*. Konserva banka silindr shaklida bo‘lib, uning to‘la sirti 216 π cm2 ga teng. Bankaga eng ko‘p suv sig‘ishi (ketishi) uchun banka asosining radiusi va balandligi qanday bo‘lishi kerak?
80. To‘g‘ri to‘rtburchak shaklidagi maydonning yuzi 6400 m2. Maydonning tomonlari qanday bo‘lganda uni o‘rash uchun eng kam panjara zarur bo‘ladi?
81*. Radiusi 5m bo‘lgan sharga eng kichik hajmli konus tashqi chizilgan. Konusning balandligini toping.
82*. Metalldan sig‘imi 13,5 l, asosi kvadratdan iborat bo‘lgan to‘g‘ri bur chakli parallelepiped yasalmoqda. Idishning o‘lchamlari qanday bo‘lganda uni yasash uchun eng kam metall ketadi?
4
t 3
83. Moddiy nuqta s t( ) =
− ![]() +5t qonuniyat bilan harakatlanmoqda (s(t)
+5t qonuniyat bilan harakatlanmoqda (s(t)
4
metrda, vaqt t sekundda o‘lchanadi). Quyidagilarni toping:
1) eng katta tezlanishga erishiladigan t0 vaqtni;
2) t0 vaqtdagi oniy tezlikni;
3) t0 vaqt ichida bosib o‘tilgan yo‘lni.
t4 3
84. Moddiy nuqtas t( ) =
− ![]() +12t qonuniyat bilan harakatlanmoqda (s(t) m 2
+12t qonuniyat bilan harakatlanmoqda (s(t) m 2
da,vaqt t sekundda o‘lchanadi).
1) eng katta tezlanishga erishiladigan t0 vaqtni;
2) t0 vaqtdagi oniy tezlikni;
3) t0 vaqt ichida bosib o‘tilgan yo‘lni toping.
t3 2
85. Moddiy nuqta s t( ) = ![]() −2t +
40t
+50 qonuniyat bilan harakatlan- 9
−2t +
40t
+50 qonuniyat bilan harakatlan- 9
moqda (s(t) metrda, vaqt t sekundda o‘lchanadi).
1) eng kichik tezlikka erishiladigan t0 vaqtni;
2) t0 vaqtdagi tezlanishni;
3) t0 vaqt ichida bosib o‘tilgan yo‘lni toping.
t3 2
86. Moddiy nuqta s t( )= − + +3t 8t 5 qonuniyat bilan harakatlanmoqda 2
(s(t) metrda, vaqt t sekundda o‘lchanadi). Quyidagilarni toping:
1) eng kichik tezlikka erishiladigan t0 vaqtni;
2) t0 vaqtdagi tezlanishni;
3) t0 vaqt ichida bosib o‘tilgan yo‘lni.
87. Havo shariga t ∈ [0; 10] minut oralig‘ida V(t)=5t3+3t2+2t+4 (m3) havo purkalmoqda.
1) boshlang‘ich vaqtdagi havo hajmini;
2) t =10 minutdagi havo hajmini;
3) t =5 minutdagi havo purkash tezligini toping;
88. Havo shariga t ∈ [0; 15] minut oralig‘da V(t)=t3+13t2+t+20 (m3) havo purkalmoqda.
1) boshlang‘ich vaqtdagi havo hajmini;
2) t=15 minutdagi havo hajmini;
3) t=10 minutdagi havo purkash tezligini toping;
89. Muslima shim tikish uchun buyurtma oldi. U bir oyda x ta shim tiksa, p(x)=–2x2+120x ming so‘m daromad qiladi. Quyidagilarni toping:
1) daromadni eng katta qilish uchun qancha shim tikishi kerak? 2) eng katta daromad qancha bo‘ladi?
90. Muxlisa yubka tikish uchun buyurtma oldi. Bir oyda x ta yubka tiksa, p(x)=–3x2+96x (ming so‘m) daromad qiladi. Quyidagilarni toping:
1) daromadni eng katta qilish uchun qancha yubka tikish kerak?
2) eng katta daromad qancha bo‘ladi?

y=f(x) funksiya x0 nuqtada chekli f ′(x0) hosilaga ega bo‘lsin.
x0 abssissali nuqtada y=f(x) funksiya grafigiga o‘tkazilgan urinma
tenglamasi y–f(x0)=f ′(x0)(x–x0) kabi yozilishini bilamiz.
x0 nuqta yaqinida y=f(x) funksiya grafigini urinmaning mos kes masi bilan almashtirsa bo‘ladi (29-rasmga qarang):
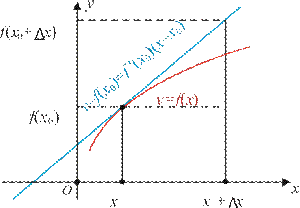
0 0
29-rasm.
x − x0 orttirmani ∆x deb belgilasak (ya’ni x = x0 + ∆x deb olsak) quyidagi taqribiy munosabatga ega bo‘lamiz:
f ( x) ≈ f ( x0 ) + f ′( x0 )(x − x0 ), yoki f (x0 + ∆x) ≈ f (x0 )+ f ′(x0 )⋅∆x (1)
(1) taqribiy formula kichik orttirmalar formulasi deb nomlanadi.
Izoh. x0 nuqta sifatida f x( 0 ), f ′(x0 ) qiymatlar oson hisoblanadigan nuqtani tanlab olish tavsiya etiladi. Shu bilan birga x nuqta x0 ga qancha yaqin bo‘lsa, bunday almashtirish aniqroq bo‘lishini qayd etamiz.
Endi biz kichik orttirmalar formulasiga tayangan holda taqribiy hisoblashlarni bajaramiz.
1-misol. f(x) = x7–2x6+3x2–x+3 funksiyaning x = 2,02 nuqtadagi qiymatini taqribiy hisoblang.
r x = 2,02 nuqtaga yaqin bo‘lgan x0 = 2 nuqtani olsak, bu nuqtada
f(x) funksiya qiymati osonlikcha topiladi: f ( x0 ) = f (2) =13.
Bu funksiyaning hosilasini topamiz: f '(x) = 7x6 −12x5 + −6x 1.
U holda f ′(x0) = f ′(2) = 75, Δx=x – x0=2,02 – 2=0,02 bo‘ladi.
Demak, (1) formulaga ko‘ra f (2,02)=f (2+0,02)≈13+75·0,02=14,5.
![]() Kalkulator yoki
boshqa hisoblash vositasi yordamida f (2,02)≈14,57995
qiymatni hosil qilishimiz mumkin. ▲ 2-misol. 1,02 ildizning
qiymatini taqribiy hisoblang.
Kalkulator yoki
boshqa hisoblash vositasi yordamida f (2,02)≈14,57995
qiymatni hosil qilishimiz mumkin. ▲ 2-misol. 1,02 ildizning
qiymatini taqribiy hisoblang.
r f
(
)x = x funksiyani qaraymiz. Uning hosilasini topamiz: f '(x) ![]() .
.
![]() x0 = 1 deb olsak, f
(
x0 )
=
f
(1)
=
=1 1,
x0 = 1 deb olsak, f
(
x0 )
=
f
(1)
=
=1 1,
f
'(
x0
) ![]() f
'(1) bo‘ladi.
f
'(1) bo‘ladi.
Demak, (1) formulaga ko‘ra
![]() .
.
Kalkulator yoki boshqa hisoblash vositasi yordamida
![]() 1,02 ≈1,0099504938... qiymatni hosil qilishimiz mumkin. ▲
1,02 ≈1,0099504938... qiymatni hosil qilishimiz mumkin. ▲
![]() 3-misol. 3
7.997 ning qiymatini taqribiy hisoblang.
3-misol. 3
7.997 ning qiymatini taqribiy hisoblang.
r f ( )x = 3 x funksiyani qaraymiz. Uning hosilasini topamiz:
![]() f
'(
)x =
f
'(
)x = ![]() x−
x−![]() . x0 = 8 deb olsak, f
(
x ) = f (8)
=
8
=
2,
. x0 = 8 deb olsak, f
(
x ) = f (8)
=
8
=
2,
f '(x0 ) = f '(8) =
∆ =x 7,997 − =−8 0,003 bo‘ladi.
Demak, (1) formulaga ko‘ra
![]() .
.
Kalkulator yoki boshqa hisoblash vositasi yordamida
![]() qiymatni hosil
qilishimiz mumkin. ▲
qiymatni hosil
qilishimiz mumkin. ▲
4-misol. sin 29° ning qiymatini taqribiy hisoblang.
r f ( )x =sinx funksiyani qaraymiz. Uning hosilasini topamiz:
f '( x ) = cos x.
π π π 1
![]()
![]()
![]()
![]() x0
=
x0
= ![]() deb olsak, f x(
=
sin = ,
deb olsak, f x(
=
sin = ,
6 6 2
0 π π ∆ =x − = − bo‘ladi. f '(x ) = f ' = cos =
6 6 2
Demak, (1) formulaga ko‘ra
![]()
Kalkulator yoki boshqa hisoblash vositasi yordamida sin29o ≈ 0,4848096202... qiymatni hosil qilishimiz mumkin. ▲
5-misol. Logarifmlarni hisoblash uchun kichik orttirmalar formulasini keltiramiz.
r f(x)=lnx; f ′(x)
= ![]() 1 . (1) ga ko‘ra, ln(x0
+
∆x) ≈ lnx0
+
1
⋅∆x – x x0
1 . (1) ga ko‘ra, ln(x0
+
∆x) ≈ lnx0
+
1
⋅∆x – x x0
kichik orttirmalar formulasini hosil qilamiz.
Agar x0 =1 va ∆x =t bo‘lsa, ln(1+t) ≈ t bo‘ladi.
Bundan, masalan, ln1,3907= ln(1+0,3907) ≈ 0,3907 qiymatni olamiz.
Agar x0 =0, ya’ni ∆ =x x − x0 = x bo‘lsa, (1) kichik orttirmalar formulasi f(x)≈f(0)+f ′(0)x (2)
ko‘rinishni oladi. ▲
Sinfda bajariladigan topshiriq. (2) formulaga asoslanib, x yetarlicha kichik bo‘lganda
sinx≈x, tgx≈x, ex≈1+x, (1+x)m≈1+mx, jumladan, ![]() x
,
x
,
![]() x taqribiy formulalarni hosil qiling.
x taqribiy formulalarni hosil qiling.
6-misol. ![]() ifodani taqribiy
hisoblang.
ifodani taqribiy
hisoblang.
r (1+x)m ≈ 1+mx formuladan foydalanamiz:
![]() = (1–0,003)–30 ≈
1+(–30)(–0,003)=1+0,09=1,09.
= (1–0,003)–30 ≈
1+(–30)(–0,003)=1+0,09=1,09.
Kalkulator yoki boshqa hisoblash vositasi yordamida
![]() qiymatni hosil
qilishimiz mumkin. ▲
qiymatni hosil
qilishimiz mumkin. ▲
(1+x)m ≈ 1+mx taqribiy formuladan foydalanib ildizlarni tezkor hisoblash usulini taklif qilish mumkin.
![]()
![]() Chindan
ham, n – natural son bo‘lib, B soni An ga nisbatan yetarlicha kichik bo‘lsin.
Chindan
ham, n – natural son bo‘lib, B soni An ga nisbatan yetarlicha kichik bo‘lsin.
U holda
1
![]()
![]()
![]() n n B
n B
yoki
n n B
n B
yoki
A + B = A1+ n ≈ A1+ n
A nA
![]() n B
n
A
+
B
≈
A+
n B
n
A
+
B
≈
A+
![]() n−1 .
n−1 .
nA
Masalan, ![]()
![]() Kalkulator
yoki boshqa hisoblash vositasi yordamida 3 125
=
5,0788... qiymatni hosil qilishimiz mumkin.
Kalkulator
yoki boshqa hisoblash vositasi yordamida 3 125
=
5,0788... qiymatni hosil qilishimiz mumkin.
(2) formulaga asoslanib, x yetarlicha kichik bo‘lganda cosx ning qiymatini taqribiy hisoblaylik. (cos x)ʹ = – sin x bo‘lgani uchun f(x) ≈ f(0)+f ʹ(0)x formula cosx≈cos0–(sin0)x=1, ya’ni cosx≈1 ko‘rinishni oladi. Ravshanki, bunday “taqribiy” formula bizni qanoatlantirmaydi. Shuning uchun, boshqacha yo‘l tutamiz. Asosiy trigo nometrik ayniyatdan cosx = ± 1−sin2 x tenglikni hosil qilamiz.
![]() Yuqorida
qayd etganimizdek, x yetarlicha kichik bo‘lganda sinx≈x bo‘ladi.
Demak, cosx=
−1
sin2
x≈ −1
x2 .
Yuqorida
qayd etganimizdek, x yetarlicha kichik bo‘lganda sinx≈x bo‘ladi.
Demak, cosx=
−1
sin2
x≈ −1
x2 .
Ravshanki, x yetarlicha kichik bo‘lganda x2 ham kichik bo‘ladi.
![]() 2
2
![]() Demak,
Demak, ![]() x formuladan 1− x2
≈
−1 x formula bevosita
x formuladan 1− x2
≈
−1 x formula bevosita
2 2 x kelib chiqadi, ya‘ni cosx≈ −1 formula o‘rinli bo‘ladi.
2
7-misol. cos44° ni taqribiy hisoblang.
r cos(x–y)=cosxcosy+sinxsiny bo‘lgani uchun
![]()
![]() ,
,
![]() .
.
Demak, cos44° ≈ 0,7193403....
Kalkulator yoki boshqa hisoblash vositasi yordamida cos44°≈0,7193339... qiymatni hosil qilamiz.
1. Kichik orttirmalar formulasini yozing.
2. Kichik orttirmalar formulasining tatbiqiga oid misollar keltiring.
91. f ( x) funksiyaning x1 va x2 nuqtalardagi qiymatini taqribiy
|
hisoblang: |
|
|
|
a) f(x)=x4+2x, |
x1=2,016, |
x2=0,97; |
|
b) f(x)=x5–x2, |
x1=1,995, |
x2=0,96; |
|
d) f(x)=x3–x, |
x1=3,02, |
x2=0,92; |
|
e) f(x)=x2+3x, |
x1=5,04, |
x2=1,98. |
(1+x)m≈1+mx taqribiy formuladan foydalanib, sonli ifoda qiymatini hisoblang (92–93):
92. a) 1,002100; b) 0,9956; d) 1,03200; e) 0,99820.
93.
![]()
![]()
![]() a) 1,004; b) 25,012; d) 0,997; e) 4,0016.
a) 1,004; b) 25,012; d) 0,997; e) 4,0016.
Taqribiy formulalardan foydalanib, hisoblang (94 – 97):
94. a) tg 44°; b) cos 61°; d) sin 31°; e) ctg 47°.
π π
95.
a) cos ![]() + 0,04
; b) sin
+ 0,04
; b) sin ![]() − 0,02
;
− 0,02
;
6 6
π π
c) sin ![]() + 0,03
; d) tg
+ 0,03
; d) tg ![]() − 0,05
.
− 0,05
.
6 6
96.
a)![]() ; b)
; b)![]() ; d)
; d)![]() ;; e)
;; e)![]() .
.
97.
а) ln0,9; b) e0,015
; d) ![]() .
.
y = f ( x) ning ko‘rsatilgan nuqtadagi taqribiy qiymatini hisoblang
(98 – 106):
98. ![]() y
= x =1,012.
y
= x =1,012.
99. y = x =1,97.
|
100. y x= 3, |
|
|
x=1,021. |
|
101. y x= 4, |
|
|
x= 0,998. |
|
|
|
|
x =1,03. |
|
103. y = x6, |
|
|
x = 2,01. |
104*. y= + +1 x sin ,x x = 0,01.
![]() 105*. y= 3
3x+
cos
,x x = 0,01.
105*. y= 3
3x+
cos
,x x = 0,01.
106*. y= 4 2x−sin(πx / 2), x=1,02.

10-sinfda (79 – 81 mavzu) bakteriyalar sonining ko‘payish jarayonini o‘rgandik. Endi bu hodisaga boshqacha yondashaylik.
1-masala. Har bir bakteriya ma’lum vaqtdan (bir necha soat yoki minutlardan) so‘ng ikkiga bo‘linadi va bakteriyalar soni ikki karra ortadi. Navbatdagi vaqtdan so‘ng mazkur ikkita bakteriya ham ikkiga bo‘linadi va populatsiya miqdori (bakteriyalar umumiy soni) yana ikki karra ortadi... Bu ko‘payish jarayoni qulay (populatsiya uchun zarur resurslar, joy, oziqa, suv, energiya va hokazolar yetarli bo‘lgan) sharoitlarda davom etaveradi, deylik.
Bakteriyalarning ko‘payish tezligi bakteriyalar umumiy soniga proporsional deb faraz qilaylik.
Bakteriyalar populatsiyasining soni ixtiyoriy t vaqtga nisbatan qanday o‘zgaradi?
r b(t) deb t vaqt oralig‘idagi bakteriyalar populatsiyasining umumiy sonini belgilaylik.
Hosilaning ma’nosiga ko‘ra, bakteriyalar ko‘payish tezligi b′(t) ga teng.
Farazimizga ko‘ra, ixtiyoriy t vaqtda b′(t) miqdor b(t) miqdorga proporsional, ya’ni
b′(t)=kb(t) (1)
munosabat o‘rinli. Bu yerda k – proporsionallik koeffitsiyenti.
b0 = b(0) – boshlang‘ich t = 0 vaqtdagi populatsiya soni bo‘lsin.
Ravshanki, b(t)=b0ekt funksiya (1) ni qanoatlantiradi.
Chindan ham, b′(t)=(b0ekt)′=kb0ekt=kb(t).
Dastlab 10 million bakteriya bo‘lsa (b0=10 mln), bunday bakteriyalar soni bir soatdan so‘ng b(1)=10e k=20 (mln) ga teng bo‘ladi, ya’ni ek=2. Bundan k=ln2 ga ega bo‘lamiz.
t vaqt oralig‘idagi bakteriyalar populatsiyasining sonini topaylik: b(t)=10e (ln2)t=10·2 t (mln).
Bu natija 10-sinfda olingan natija bilan ustma-ust tushmoqda. ▲
|
Tarixiy ma’lumot. 18-asrda ingliz olimi Tomas Maltus yuqoridagi fikrlarga o‘xshash fikr yuritib, yer yuzidagi aholi sonining o‘sishi uchun N ′(t)=kN(t) (2) munosabatni hosil qildi, bu yerda N(t) – vaqtning t momentidagi aholi soni. N0=N(t0) – boshlang‘ich t0 vaqtdagi aholi soni bo‘lsin. Bu holda N(t)=N 0e k(t–t0) funksiya (2) tenglamani qanoatlantiradi. Chindan ham, N ′(t)= N 0(e k(t–t0))′=kN 0e k(t–t0)=kN(t). N(t)=N 0e k(t–t0) qonuniyat aholining eksponensial o‘sishini, ya’ni shiddatli, to‘xtovsiz o‘sish jarayonini ifodalashini inobatga olib, Tomas Maltus vaqt o‘tishi bilan insoniyatga oziqa resurslari yetmasligini «bashorat” qilganligini qayd etamiz (30-rasmga qarang). |
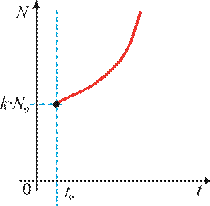
30-rasm.
2-masala. Ekologiya tirik organizmlarning tashqi muhit bilan o‘zaro munosabatini o‘rganadi. Ko‘payish yoki turli sabablarga ko‘ra nobud bo‘lish bilan bog‘liq bo‘lgan populatsiyalar sonining o‘zgarish tezligi vaqtga qanday bog‘lanishda ekanini o‘rganing.
r N(t) – vaqtning t momentidagi populatsiya soni bo‘lsin, u holda agar vaqtning bir birligida populatsiyada tug‘iladigan jonzotlar sonini A, nobud bo‘ladiganlari sonini B desak, yetarli asos bilan aytish mumkinki,
N ning vaqtga nisbatan o‘zgarish tezligi
N ′(t) =A–B (3)
munosabatni qanoatlantiradi.
Tadqiqotchilar A va B ning N ga bog‘liqligini quyidagicha tavsiflaydilar.
a) Eng sodda hol: A=aN(t), B=bN(t). Bu yerda a va b – vaqtning bir
birligida tug‘ilish va nobud bo‘lish koeffitsiyentlari.
Bu holda (3) munosabatni
N′(t) =(a–b)N(t) (4)
ko‘rinishda yozish mumkin.
N0=N(t0) – boshlang‘ich t0 vaqtdagi populatsiya soni bo‘lsin.
Bu holda N(t)=N0e(a–b)(t–t0) funksiya (4) ni qanoatlantiradi (tekshiring). b) A=aN(t), B=bN 2(t) hol ham uchraydi.
Bunda
N′(t)=aN(t) – bN 2(t) (5)
munosabat hosil bo‘ladi. N a b0 /
Tekshirish mumkinki, N t(
)= ![]() − −a
t t( 0 ) funksiya (5)
− −a
t t( 0 ) funksiya (5)
N0 +[a b/ − N0 ]e
tenglamani qanoatlantiradi. ▲
(4) munosabatni 1845-yilda belgiyalik demograf-olim Ferxyulst populatsiyadagi ichki kurashni hisobga olgan holda kashf qildi. Bu natija Maltusning (2) munosabatiga nisbatan populatsiyaning rivojlanishini aniqroq tavsiflaydi.
Populatsiyaning o‘sish-kamayishi a va b sonlarga qanday bog‘liq bo‘ladi, degan savol tug‘ilishi tabiiy.
a a
31-rasmda > N0 va < N0 hollar uchun b b
N a b0 /
N t( )= ![]() −
−a t t( 0 ) ko‘rinishdagi funksiya grafiklari N0 +[a
b/ −
N0
]e
tasvirlangan:
−
−a t t( 0 ) ko‘rinishdagi funksiya grafiklari N0 +[a
b/ −
N0
]e
tasvirlangan:
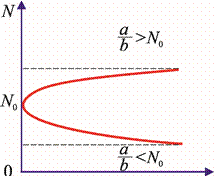
31-rasm.
a
Ko‘rinib turibdiki, vaqt kechishi bilan populatsiya soni soniga b
yaqinlashar ekan. Mazkur holat to‘yinish deb nomlangan hodisani bildiradi.
Chizmada tasvirlangan egri chiziq Maltus tomonidan logistik egri chiziq deb nomlanib, u inson turmushining turli sohalarida uchrab turadi.
Funksiyaning hosilasini shu funksiya bilan bog‘l ovchi y′(x)=F(x; y) ko‘rinishdagi munosabat differensial tenglama de yi ladi.
Yuqorida keltirilgan (1) – (5) munosabatlar differensial tenglamalarga misollardir.
Differensial tenglamani qanoatlantiradigan har qanday funksiya uning yechimi deyiladi. Oliy matematikada muayyan shartlarda y ′(x)=F(x, y) ko‘rinishdagi differensial tenglamaning y(x 0)=y 0 boshlang‘ich shartni qanoatlantiradigan yagona y(x) yechimi mavjudligi isbot qilingan.
3-masala. Vaqtning t momentida sotilayotgan mahsulot haqida xabardor bo‘lgan xaridorlar soni x(t) ning vaqtga bog‘liqligini o‘rganing. (Bu masala reklama samaradorligini aniqlashda muhim.)
r Barcha xaridorlar sonini N deb belgilasak, sotilayotgan mahsulotdan bexabarlar soni N–x(t) bo‘ladi.
Mahsulot haqida xabardor bo‘lgan xaridorlar sonining o‘sish tezligi x(t) ga va N–x(t) ga proporsional deb hisoblasak, quyidagi differensial tenglamaga ega bo‘lamiz:
x′(t)=kx(t)(N–x(t)), bu yerda k > 0 – proporsionallik koeffitsiyenti.
N
Bu tenglamaning yechimi x
t(
) = ![]() −Nkt dan iborat, bunda
−Nkt dan iborat, bunda
1+ Pe
1
P
= ![]() NC
, C – o‘zgarmas son.
NC
, C – o‘zgarmas son.
e
Ravshanki, har qanday holatda t vaqt kechishi bilan Pe–Nkt
had kichiklashib boraveradi va bundan x(t)x= ![]() N−Nkt ifodaning qiymati N ga
N−Nkt ifodaning qiymati N ga
1+Pe yaqinlashadi (32-rasmga qarang). ▲
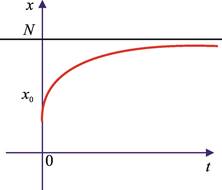
32-rasm.
4-masala. Massasi m, issiqlik sig‘imi c o‘zgarmas bo‘lgan jism boshlang‘ich momentda T0 temperaturaga ega bo‘lsin. Havo temperaturasi o‘zgarmas va τ (T > τ) ga teng. Jismning cheksiz kichik vaqt ichida bergan issiqligi jism va havo temperaturalari orasidagi farqqa, shuningdek, vaqtga proporsional ekanligini e’tiborga olgan holda, jismning sovish qonunini toping.
r Sovish davomida jism temperaturasi T0 dan τ gacha pasayadi. Vaqtning t momentida jism temperaturasi T(t) ga teng bo‘lsin. Cheksiz kichik vaqt oralig‘ida jism bergan issiqlik miqdori, yuqorida aytilganiga ko‘ra,
Q'(t)=–k(T–τ)
ga teng, bu yerda k – proporsionallik koeffitsiyenti.
Ikkinchi tomondan, fizikadan ma’lumki, jism T temperaturadan τ temperaturagacha soviganda beradigan issiqlik miqdori Q=mc(T(t)–τ) ga teng. Hosilani hisoblaymiz:
Q ′(t)=mcT ′ (t). (6)
Q′(t) uchun topilgan har ikkala ifodani taqqoslab, mcT ′(t)=–k(T–τ) differensial tenglamani hosil qilamiz.
k
− ![]() t
t
funksiya (6) differensial tenglamani qanoatlantiradi (o‘zingiz tekshiring!), bu yerda C – ixtiyoriy o‘zgarmas son.
Boshlang‘ich shart (t = 0 da T = T0) C ni topishga imkon beradi:
C=T0 – τ.
Shuning uchun jismning sovish qonuni quyidagi ko‘rinishda yoziladi:
k
− ![]() t
t
T(t)= τ+(T0 – τ) e mc.
k − ![]() t
t
Javob: T(t)= τ+(T 0 – τ) e mc ▲.
5-masala. Tandirdan olingan (uzilgan) nonning temperaturasi 20 minut ichida 100° dan 60° gacha pasayadi. Tashqi muhit temperaturasi 25°.
Nonning temperaturasi qancha vaqtda 30° gacha pasayadi?
r Yuqoridagi masalaning yechimidan foydalanib, nonning sovish qonunini quyidagi ko‘rinishda yoza olamiz:
k
− ![]() t
t
T(t)= τ+(T0 – τ) e mc = +25 100 25( − )eat = +25 75eat ,
bu yerda a – noma’lum koeffitsiyent. a ni topish uchun t = 20 da T(20) = 60 tenglikdan foydalanamiz: T (20) = 25 + 75e20a = 60,
![]()
75e20a = 35, (ea )20 = 3575 = 157 , ea = 157 .
t
![]()
7
20
7
20
Demak, nonning sovushi T = 25+ 75 qonuniyatga bo‘ysunar ekan.
15
Nonning temperaturasi 30° gacha pasayish vaqtini topamiz:
t t
![]() 30
25 75= +
7
20
, 7
20
=
5
=
1
,
30
25 75= +
7
20
, 7
20
=
5
=
1
,
15 15 75 15
t
![]() 7
20 t
7
20 t
ln = (ln(7)−ln 15 )( )
15 20
bo‘lgani uchun t![]() .
.
Javob: 1 soat-u 11 minutda nonning temperaturasi 30° gacha pasayadi. ▲
6-masala. Motorli qayiq turg‘un suvda 20 km/soat tezlik bilan harakatlanmoqda. Ma’lum vaqtdan keyin motor ishdan chiqdi. Motor to‘xtagandan 40 sekund vaqt o‘tgach qayiqning tezligi 8 km/soat bo‘ldi.
Suvning qarshiligi tezlikka proporsional bo‘lsa, motor to‘xtagandan 2 minut vaqt o‘tgach qayiq tezligini toping.

r Qayiqqa F = – kv kuch ta’sir qilmoqda. Nyuton qonuniga ko‘ra F=mv ′(t) Bundan mv ′ (t) = – kv.
k
− ![]() t
t
Bu tenglamani v t( ) = Ce m ko‘rinishdagi funksiya qanoatlantiradi.
t = 0 da v = 20 shartidan C = 20 kelib chiqadi.
r
− ![]() t
t
![]()
![]() Bundan v t( ) =
20e
m . t = 40 s = soat bo‘lganda qayiqning
Bundan v t( ) =
20e
m . t = 40 s = soat bo‘lganda qayiqning
r 90
![]() m
= 5
hamda tezligi 8 km/soatga
teng, bundan 8 = 20e yoki e
m
= 5
hamda tezligi 8 km/soatga
teng, bundan 8 = 20e yoki e
![]()
1 5 90 5 −3 32
![]() t
=
2min
=
t
=
2min
=![]() soat bo‘lganidan v =
20
soat bo‘lganidan v =
20 ![]()
= 20 = ≈1,28
= 20 = ≈1,28
30 2 2 25
(km/s) ekanini topamiz.
Javob: Motor to‘xtaganidan 2 minut vaqt o‘tgach, qayiqning tezligi taxminan 1,28 km/soat ga teng bo‘ladi. ▲
7-masala. Radioaktiv yemirilish natijasida radioaktiv modda massasi m(t) ning vaqtga nisbatan o‘zgarish qonuniyatini toping. Bu yerda m(t) gramm, t – yillarda o‘lchanadi.
r Yemirilish tezligi massaga proporsional deb faraz qilsak,
m′(t) = – α m(t) (7)
differensial tenglamaga ega bo‘lamiz. m(t)=Ce–αt funksiya bu tenglamaning yechimi ekanligini tekshirish mumkin.
m(t0) = m0 boshlang‘ich shartdan m t( ) = m e0 −α (t t− 0 ) qonuniyatga ega
bo‘lamiz. Javob: m t( ) = m e0 −α (t t− 0 ) . ▲
Iqtisodiy modellar. Talab va taklif iqtisodiyotning fundamental (asosiy) tushunchalaridir.
Talab (tovarlar va xizmatlarga talab) – xaridor, iste’molchining bozordagi muayyan tovarlarni, ne’matlarni sotib olish istagi; bozorga chiqqan va pul imkoniyatlari bilan ta’minlangan ehtiyojlari.
Talab miqdorining o‘zgarishiga bir qancha omillar ta’sir qiladi. Ularning orasida eng muhimi narx omilidir. Tovar narxining pasayishi sotib olinadigan tovar miqdorining o‘sishi va aksincha, narxning o‘sishi xarid miqdorining kamayishiga olib keladi.
Taklif — muayyan vaqtda va muayyan narxlar bilan bozorga chiqarilgan va chiqarilishi mumkin bo‘lgan tovarlar va xizmatlar miqdori bilan ifoda etiladi; taklif – ishlab chiqaruvchi (sotuvchi)larning o‘z tovarlarini bozorda sotishga bo‘lgan istagi. Bozorda tovar narxi bilan uning taklif miqdori o‘rtasida bevosita bog‘liqlik mavjud: narx qanchalik yuqori bo‘lsa, boshqa sharoitlar o‘zgarmagan hollarda, sotish uchun shuncha ko‘proq tovar taklif etiladi, yoki aksincha, narx pasayishi bilan taklif hajmi qisqaradi.
Talab va taklifninng tub mazmuni ularning narx orqali o‘zaro aloqadorlikda mavjud bo‘lishidir. Bu aloqadorlik — talab va taklif qonuni bozor iqtisodiyotining obyektiv qonuni hisoblanadi. Talab va taklif qonuniga ko‘ra, bozordagi taklif va talab faqat miqdoran emas, balki o‘zining tarkibi jihatidan ham bir-biriga mos kelishi kerak, shundagina bozor muvozanatiga erishiladi. Bu qonun ayirboshlash qonuni bo‘lib, bozorni boshqaruvchi va tartiblovchi kuch darajasiga ko‘tariladi. Unga ko‘ra bozordagi talab o‘zgarishlari darhol ishlab chiqarishga yetkazilishi kerak. Bozordagi talab va taklif nisbatiga qarab ishlab chiqarish sur’atlari va tuzilmasi tashkil topadi.
Quyidagi masalani qaraylik.
Fermer uzoq muddat davomida mevalarni bozorda sotishga chiqarib keladi. Har hafta yakunida u narxning o‘zgarish tezligini kuzatib, kelgusi haftaga chiqariladigan mevalarning yangi narxini chamalaydi.
Xuddi shunday iste’molchilar ham narxning o‘zgarish tezligini kuzatib, kelgusi haftaga sotib olinadigan mevalarning miqdorini belgilaydilar.
Kelgusi haftadagi mevalarning narxini p orqali, narxning o‘zgarish tezligini esa p′ orqali belgilaylik.
Taklif ham, talab ham tovar narxi bilan uning o‘zgarish tezligiga bog‘liq ekanligini ishonch bilan aytishimiz mumkin. Bu bog‘lanish qanday bo‘ladi?
r Bunday bog‘lanishlarning eng sodda ko‘rinishi quyidagicha bo‘lar ekan: y=ap′+bp+c, bu yerda a, b, c – haqiqiy sonlar.
Masalan, q orqali talabni, s orqali esa taklifni belgilasak, ular uchun yuqoridagi bog‘lanishlar q=4p′–2p+39, s=44p'+2p–1 tenglamalar yordamida ifodalanishi mumkin.
Bu holda talab va taklifning o‘zaro tengligi 4p′–2p+39 = 44p′+2p–1 munosabat yordamida ifodalanadi. p −10
Bu tenglikdan p'
=
− ![]() ko‘rinishdagi differensial tenglamani
ko‘rinishdagi differensial tenglamani
hosil qilamiz. 10
Agar boshlang‘ich narxni p(0)=p0 deb belgilasak, narx
t
− ![]() p=
(
p0 −10)e
10 +10 qonuniyat bilan o‘zgarishini hosil qilamiz. ▲
p=
(
p0 −10)e
10 +10 qonuniyat bilan o‘zgarishini hosil qilamiz. ▲
Investitsiya. Faraz qilaylik, qandaydir mahsulot p narx bilan sotiladi, Q(t) funksiya t vaqt mobaynida ishlab chiqarilgan mahsulot miqdori o‘zgarishini bildiradi desak, u holda t vaqt davomida pQ(t) ga teng daromad olinadi. Aytaylik, olingan daromadning bir qismi mahsulot ishlab chiqarish investitsiyasiga sarf bo‘lsin, ya’ni
I t( ) = mpQ t( ) , (8)
m – investitsiya normasi, o‘zgarmas son va 0<m<1.
Agar bozor yetarlicha ta’minlangan va ishlab chiqarilgan mahsulot to‘la sotilgan degan tasavvurdan kelib chiqilsa, bu holat ishlab chiqarish tezligining yana oshishiga olib keladi.
Ishlab chiqarish tezligi esa investitsiyaning o‘sishiga proporsional, ya’ni
Q′ = l · I(t), (9)
bu yerda l – proporsionallik koeffitsiyenti.
(8) formulani (9) ga qo‘yib
Q kQ' = , k = lmp (10)
differensial tenglamani hosil qilamiz.
C – ixtiyoriy o‘zgarmas son bo‘lganda Q Ce= kt ko‘rinishdagi funksiya
(10) differensial tenglamani qanoatlantiradi.
Faraz qilaylik, boshlang‘ich moment t = t0 da mahsulot ishlab chiqarish hajmi Q0 berilgan. U holda bu shartdan o‘zgarmas C ni topish mumkin:
Q0 = Cekt0 , bundan C = Q e0 −kt0 .
Natijada ishlab chiqarish hajmi Q Qe= 0 k t t( − 0 ) qonuniyat bilan o‘zgarishini bilib olamiz.
1. Bakteriyalarning ma’lum vaqtdan so‘ng ikkiga bo‘lina borishi jarayonini hosila yordamida modellashtiring.
2. Tomas Maltusning yer yuzidagi aholi soni o‘sishiga oid masalasini tushuntiring.
3. Tomas Maltusning logistik egri chizig‘ini tushuntiring.
4. Reklama samaradorligiga oid masalani hosila yordamida modellashtiring.
Matndagi 4-masala yechimidan foydalanib, mashqlarni bajaring (107–108):
107. Temperaturasi 25°C bo‘lgan metall parchasi pechga qo‘yildi.
Pechning temperaturasi 25°C dan boshlab minutiga 20°C tezlik bilan tekis
ravishda ko‘tarila boshladi. Pech va metall temperaturasining farqi T°C
bo‘lganda, metall minutiga 10![]() T°C tezlik bilan isitila boshlaydi.
T°C tezlik bilan isitila boshlaydi.
Metall parchasini 30 minutdan keyingi temperaturasini toping.
108. Jismning boshlang‘ich temperaturasi 5°C. Jism N minut davomida 10°C gacha isidi. Atrof-muhit temperaturasi 25°C bo‘lib turibdi. Jism qachon 20°C gacha isiydi?
Matndagi 7-masala yechimidan foydalanib, mashqlarni bajaring:
109. Tajribalarga ko‘ra 1 yil davomida radiyning har bir grammidan
0,44 mg modda yemiriladi
a) necha yildan so‘ng mavjud radiyning 20 foizi yemiriladi?
b) mavjud radiyning 400 yildan so‘ng necha foizi qoladi?
Matndagi 6-masalani yechishdagi mulohazalardan foydalanib, mashqlarni bajaring (110 – 111):
110. Qayiq suvning qarshiligi ta’siri ostida o‘z harakatini sekinlashtiradi. Suv ning qarshiligi qayiq tezligiga proporsional. Qayiqning boshlang‘ich tezligi 1,5 m/s. 4 sekunddan so‘ng uning tezligi 1 m/s ni tashkil qildi.Necha sekunddan so‘ng qayiqning tezligi 2 marta kamayadi?
111. 10 l hajmdagi idish havo bilan to‘ldirilgan (80% azot, 20% kislorod). Shu idishga 1 sekundda 1 litr tezlikda azot purkalmoqda. U uzluksiz ravishda aralashib, shu tezlikda idishdan chiqmoqda. Qancha vaqtdan so‘ng idishda 95% azotli aralashma hosil bo‘ladi?
Ko‘rsatma: y(t) bilan t vaqtdagi azot ulushini belgilasak, y(t) funksiya y ′ ·V=a(1–y) munosabatni qanoatlantiradi deylik. Bu yerda V – isitish hajmi, a – purkash tezligi.
1. Asosi kvadrat bo‘lgan to‘g‘ri burchakli parallelepiped shaklidagiusti ochiq metall idish yasashmoqchi. Idish hajmi 270 l bo‘lishi kerak. Idishning o‘lchamlari qanday bo‘lganda uni yasashda eng kam metall ketadi?
t4 3
2. Moddiy nuqta s t( ) =
− ![]() +72t qonuniyat bilan harakatlanmoqda 4
+72t qonuniyat bilan harakatlanmoqda 4
(s(t) metrda, t vaqt sekundda o‘lchanadi).
1) eng katta tezlanishga erishadigan vaqtni (t0);
2) t0 vaqtdagi oniy tezlikni;
3) t0 vaqt mobaynida bosib o‘tilgan yo‘lni toping.
3. Taqribiy hisoblash formulasidan foydalanib ln 0,92 ni toping.
4. Taqribiy hisoblash formulasidan foydalanib sin(–1; 2)ni toping.
5. Mahsulot ishlab chiqaruvchi tadbirkorning kunlik daromadi quyidagi formula bilan hisoblanadi:
P(x)= –3x2 + 42x – 6 (ming so‘m), bu yerda x – mahsulotlar soni.
Quyidagilarni aniqlang:
1) eng katta daromad olish uchun tadbirkor nechta mahsulot ishlab chiqa rishi kerak?
2) tadbirkorning eng katta daromadi necha so‘mni tashkil qiladi?

112. Moddiy nuqta harakatining qonuni s=s(t) ga ko‘ra uning eng katta yoki eng kichik tezligini toping:
![]()
![]() 1) s=13t;
1) s=13t; ![]() 2) s=17t
– 5; 3) s=t2+5t+18; 4) s=t3+2t2+5t+8; 5) s=2t3+5t2+6t+3; 6) s=13t3+2t2; 7) s=t3+t2+3.
2) s=17t
– 5; 3) s=t2+5t+18; 4) s=t3+2t2+5t+8; 5) s=2t3+5t2+6t+3; 6) s=13t3+2t2; 7) s=t3+t2+3.
113. Berilgan funksiya grafigiga: 1) x0=–1; 2) x0=2,2; 3) x0=0 abssissali nuqtada o‘tkazilgan urinmani toping:
1) f(x)=12x2+5x+1; ![]() 2) f(x)=13x+4;
2) f(x)=13x+4;
![]() 3) f(x)=60;
3) f(x)=60;
![]() 4) f(x)=x3+4x.
4) f(x)=x3+4x.
114. Berilgan funksiya uchun y=–7x+2 to‘g‘ri chiziqqa parallel bo‘lgan urinma tenglamasini yozing:
1) f(x)=5x3–2x2+16; ![]() 2) f(x)=–4x2+5x+3;
2) f(x)=–4x2+5x+3; ![]() 3) f(x)=–8x+5.
3) f(x)=–8x+5.
115. Berilgan f(x) va g(x) funksiyalar grafiklarining urinmalari parallel bo‘ladigan nuqtalarini toping:
1) f (x) = 2x2–3x+4, g(x)=12x–8;
2) f (x) = 18x+19, g(x)=–15x+18;
3) f (x) = 2x+13, g(x)=4x–19;
4) f (x) = 2x3, g(x)=4x2;
5) f (x) = 2x3+3x2, g(x)=15x–17; 6) f (x) = 2x4, g(x)=4x3.
1 1
116. 1) y = ![]() funksiya grafigining x =
−
funksiya grafigining x =
− ![]() nuqtadan o‘tuvchi
urinmasi x 2
nuqtadan o‘tuvchi
urinmasi x 2
tenglamasini tuzing.
2) y = x2 parabolaning x =1 va x = 3 abssissalarga mos nuqtalari tutash tirilgan. Parabolaning ushbu 2 nuqtani tutashtiruvchi kesmaga parallel bo‘lgan urinmasi qaysi nuqtadan o‘tadi?
3) Moddiy nuqta ![]() qonuniyat bilan
harakatlanmoqda
qonuniyat bilan
harakatlanmoqda
(s – santimetrda, t – sekundda). Moddiy nuqtaning 1-sekunddagi tezlanishini toping.
117. Funksiyaning ko‘rsatilgan nuqtadagi hosilasini hisobl ang:
1) f (x)=x2–15, x0
=
− ![]() ; 2)
f
(x)
=
3cos
x , x0
=
−π ;
; 2)
f
(x)
=
3cos
x , x0
=
−π ;
![]() 3
3
3) f (x) = ![]() , x0 = −2; 4) f (x)
=
−sin
x, x0 =
− .
, x0 = −2; 4) f (x)
=
−sin
x, x0 =
− .
x
5) f (x) =
x3 −
4
, x0 = 5; 6) f (x)
=
sin
x, x0 =
![]() ;
;
![]() 1
1
7) f
(x)
= ![]() 3 , x0 = −2; 8) f (x)
=
cos5x
, x0 = ; x
3 , x0 = −2; 8) f (x)
=
cos5x
, x0 = ; x
9) f
(x)
=
−cos
2x, x0
=
−![]() .
.
118. Ko‘rsatilgan vaqtdagi tezlik va tezlanishni toping:
1) x ts( ) = 5t2 − +t 50 t0 = 2; 2) s( )t = t3 +12t2 +1, t0 =1;
![]() 3) s(t)
=
2t
+
t
3 , t0 = 5; 4) s(t)
=
8sin
t , t0
=.
3) s(t)
=
2t
+
t
3 , t0 = 5; 4) s(t)
=
8sin
t , t0
=.
119. Funksiyaning abssissasi ko‘rsatilgan nuqtadagi hosilasini hisobl ang:
1) f x( ) =
x2
−15, x0 =
![]() ; 2)
f
(x)
=
3cos
x , x0 =π;
; 2)
f
(x)
=
3cos
x , x0 =π;
|
3 3) f (x) = |
|
π 4) f (x) =
−sin x, x
= |
![]() 0 x
0 x
5) f (x) = x3 − 4 , x0 = −5 ; 6) f (x) = sin x, x0 =−;
![]() 1
1
7) f
(x)
= ![]() 3
, x0
=
2; 8) f (x)
=
cos5x
, x0 =− ; x
3
, x0
=
2; 8) f (x)
=
cos5x
, x0 =− ; x
![]()
![]() 9) f (x) =
−cos
2x, x0 =; 10) f(x)=sin2x, x0 =.
9) f (x) =
−cos
2x, x0 =; 10) f(x)=sin2x, x0 =.
120. Ko‘rsatilgan vaqtdagi tezlik va tezlanishni toping:
1) s(t)=3t2–2t+10, t0=2; 2) s(t)=t3–6t2+1, t0=1;
3) s(t)=5t+2t3, t0=5; 4)
s(t)=8cost, t0
=
![]() .
.
Berilgan funksiyaning hosilasini toping (121–122):
121. ![]()
![]() 1) f
x(
) =
−x2 +
x
+30; 2) f (x) =
sin
x − cos x;
1) f
x(
) =
−x2 +
x
+30; 2) f (x) =
sin
x − cos x; ![]() 3) f
(x)
=
x
− 1 ;
3) f
(x)
=
x
− 1 ;
x
4) f (x) =
4x −sin
x ; 5) f (x)
=
8cos
x; ![]() 6) f
x(
) =
ln
x −10x2
+
x
−1.
6) f
x(
) =
ln
x −10x2
+
x
−1.
![]() 420 2
420 2
122. 1) y = x ; 2) y = ; 3) y x= − ; 4) y = x ln x ;
x
![]()
![]() 3xsinx; 7) y =
x
+21
; 8) y = 2(10x−1)sin
x. 5) y = x
sin
x ; 6) y=e
3xsinx; 7) y =
x
+21
; 8) y = 2(10x−1)sin
x. 5) y = x
sin
x ; 6) y=e
4x π π
123. Berilgan funksiyalar uchun f '(− ), 'f ( ) sonlarni hisoblang:
2 4
1) f (x) = ex cosx; 2) f (x) = 3x +1; 3) f (x) = 2x2 + x +3;
4) f (x) = sin x + x2 ; 5) f (x) = sin x + cos x ; 6) f (x) = sin x ; 7) f x( ) = cos x + x4 ; 8) f (x) = sin 3x + cos3x.
t3 2
124. Moddiy nuqta x t( ) =
− ![]() +6t +15 qonuniyat bilan harakatlanmoqda. 6
+6t +15 qonuniyat bilan harakatlanmoqda. 6
1) tezlanish nol bo‘lgan t0 vaqtni; 2) shu t0 vaqtdagi tezlikni toping.
125*. f x( ) = x2 −13x + 2 funksiya Ox o‘qi bilan qanday burchak ostida kesishadi?
126. ![]() f ′(0) sonni toping: 1) f (x)=
x6 −4x3 +
4; 2) f x( ) =
(x
+10)6.
f ′(0) sonni toping: 1) f (x)=
x6 −4x3 +
4; 2) f x( ) =
(x
+10)6.
127. y′(x) ni toping:
1) y(x)
=
sin
2 x
; ![]() 2) y(x)
=
cos2
x;
2) y(x)
=
cos2
x; ![]() 3) y x( ) =tg2x.
3) y x( ) =tg2x.
128. Funksiyaning o‘sish va kamayish oraliqlarini toping:
1) f (x)
=
3
+
7x; 2) f (x)
=
x3
+17x
; 3) f
x(
) =
![]() x +18;
x +18;
![]() x
+
21 2 (x)
=
x(x2 +8);
x
+
21 2 (x)
=
x(x2 +8);
4) f x( ) = ; 5) f x( ) = x +5x −14 ; 6) f
x
7) f
(x)
=
−x2
−
4x
+
6; 8) f (x)
=
−
![]() 12
; x
12
; x
9) f (x) = x3 −12x2 −17x −23; 10) f (x) = 3x4 +18x3 −6;
11) f x( ) = x3 −5x2 +19x + 22 ; 12) f (x) = x4 + 7x2 .
|
129. Funksiyaning statsionar nuqtalarini toping: |
|
|
|
1) f (x)
=
3x2 −
7x
+
9
; 4) f (x) = 8x2 ; 5) f x( ) = 7 14x− ; 7) f (x) =12x3 +13x2 −16 ; |
|
3) f (x) = 5x3;
6) f (x) =27–x3; 8) f (x)=x3–6x2+9. |
130. Funksiyaning lokal maksimum va lokal mimimumlarini toping:1) f
(x)
=
x2
−
![]() x4; 2) f (x)
=14+13x2
−12x3
;
x4; 2) f (x)
=14+13x2
−12x3
;
3) f (x) = x4 −3x3 + x2 + 9 ; 4) f (x) = 2x4 − x3 + 7.
131. Funksiyaning o‘sish, kamayish oraliqlari hamda lokal maksimumva minimumlarini toping:
1) f (x)=x3– 64x; 2) f (x)=2x3–24; 3) f (x)=4x3–108x.
132. Funksiyaning eng katta va eng kichik qiymatlarini toping:
![]() 1) f (x)
=
x4 −3x2 +
2, x∈[–4; 1]; 2) f (x)
=
x5 +
6x3 +1, x∈[–1; 2];
1) f (x)
=
x4 −3x2 +
2, x∈[–4; 1]; 2) f (x)
=
x5 +
6x3 +1, x∈[–1; 2];
3)
f (x)
= ![]() x , x∈[1; 5]; 4) f (x)
=
x3 +
6x2 +
5x
+8, x∈[–3; 4].
x , x∈[1; 5]; 4) f (x)
=
x3 +
6x2 +
5x
+8, x∈[–3; 4].
x + 4
133. Funksiyaning grafigini yasang:
1) y =
x3 −
2x2 +
3x
−
2; ![]() 2) y
=
2) y
=
![]() x5
+
x5
+
![]() x3
;
x3
; ![]() 3) y
=
x4 +
4x3 .
3) y
=
x4 +
4x3 .
134. To‘g‘ri to‘rtburchak shaklidagi ekin maydonining atrofini o‘rash uchun 1000 metr panjara sotib olindi. Bu panjara yordamida eng ko‘pi bilan necha kvadrat metr maydonni o‘rab olish mumkin?
135. Tomoni 16 dm bo‘lgan kvadrat shaklidagi kartondan usti ochiqquti tayyorlandi. Bunda kartonning uchlaridan bir xil kvadratchalar kesib olindi. Qutining hajmi eng katta bo‘lishi uchun uning asosi necha santimetr bo‘lishi kerak?
136*. Konserva banka silindr shaklida bo‘lib, uning to‘la sirti 512π cm2 ga teng. Bankaga eng ko‘p suv sig‘ishi uchun banka asosining radiusi va balandligi qanday bo‘lishi kerak?
137. To‘g‘ri to‘rtburchak shaklidagi maydoning yuzi 3600 m2. Maydonning tomonlari qanday bo‘lganda uni o‘rash uchun eng kam panjara zarur bo‘ladi?
138*. Radiusi 8 dm bo‘lgan sharga eng kichik hajmli konus tashqi chizilgan.
Shu konus balandligini toping.
139*. Asosi kvadrat bo‘lgan to‘g‘ri burchakli parallelepiped shaklidagi ochiq metall idishga 32 l suyuqlik ketadi. Idishning o‘lchamlari qanday bo‘lganda uni yasashga eng kam metall sarflanadi?
t4 3
140.
Moddiy nuqta s
t(
) =
− ![]() +10t qonuniyat bilan
harakatlanmoqda
+10t qonuniyat bilan
harakatlanmoqda
4
(s(t) metrda, t sekundda o‘lchanadi).
1) eng katta tezlanishga erishadigan (t0) vaqtni;
2) t0 vaqtdagi oniy tezlikni;
3) t0 vaqtda bosib o‘tilgan yo‘lni toping.
141. Havo shariga t∈[0;10] minut oralig‘da V(t) = t 3+3t 2+2t+4 m3 havo purkalmoqda.
1) boshlang‘ich vaqtdagi havo hajmini;
2) t = 10 minutdagi havo hajmini;
3) t = 5 minutdagi havo purkash tezligini toping.
142. Akrom shim tikish uchun buyurtma oldi. Bir oyda x ta shim tiksa, p(x) = – 2x2+240x (ming so‘m) daromad qiladi.
1) daromadni eng katta qilish uchun qancha shim tikish kerak?
2) eng katta daromad necha so‘m bo‘ladi?
143. Funksiyaning hosilasini toping:
1) ![]()
![]()
![]() y=e3x
; 2) y=esin
x ; 3) y
=
sin
(3x
+
2); 4) y = (2x
+1)4
;
y=e3x
; 2) y=esin
x ; 3) y
=
sin
(3x
+
2); 4) y = (2x
+1)4
;
x − 2 ln x2
5) y
= 2 ; 6) y= ![]() ; 7) y = arctg2x; 8) y
=
x ⋅cos
x. x +1 x
; 7) y = arctg2x; 8) y
=
x ⋅cos
x. x +1 x
144. f (x) = e2x va g(x) = 4x + 2 funksiyalar uchun F(x) murakkab
|
funksiyani tuzing: |
|
|
|
1) F(x)= f (g(x)); |
|
2) F(x)= f (x)g(x) ; |
|
3) F(x)= g(f (x)); |
|
|
145. Murakkab funksiyaning hosilasini toping:
1) y = (x2 +1)5 ; 2) y=lncosx;
![]()
![]() 3) y
= 5x
−
7
; 4) y
=
tg
2(
x
−3)
;
3) y
= 5x
−
7
; 4) y
=
tg
2(
x
−3)
;
5) y=arctg(3x–4); 6*) y=sin(arctg2x);
7) y =sin3 x + cos 3x; 8*) y = esin (cos x).
146. Funksiyaning o‘sish va kamayish oraliqlarini toping:
1) y = 2+
x
−
x2 ; 2) y
=
![]() (x
≥
0);
(x
≥
0);
x +100
3) y = 3x − x3 ; 4) y = 2x − sin x;
2x x2
5) y = ![]() 2
; 6) y
=
2
; 6) y
= ![]() x ;
x ;
1+ x 2
7) y = (x −1)3; 8) y = (x −1)4.
147. Funksiyaning statsionar nuqtalari, lokal maksimum va lokal mini-mumlarini toping:
3 2 2x
1) y = x −6x +9x −4; 2) y = 2 ;
1+ x
![]() 1 2
1 2
3) y
=
x
+ ![]() ; 4)
y
= 2x
−
x
. x
; 4)
y
= 2x
−
x
. x
148. Funksiyaning ko‘rsatilgan oraliqdagi eng katta va eng kichik qiy-matlarini toping:
1) f (x)= 2x , [−1; 5]; 2) f (x)= x2 −4x +6 , [–3; 10];
![]() 3) f
(x)=
x
+
3) f
(x)=
x
+ ![]() 1
, [0,01; 100]; 4) f (x)= 5
−
4x
, [−1;
1]; x
1
, [0,01; 100]; 4) f (x)= 5
−
4x
, [−1;
1]; x
![]() 5) f (x)
=
cos
x, −
5) f (x)
=
cos
x, −
![]() π2;
π; 6) f (x)=
x
−3x
+
2
, [–10; 10]; 7) f (x)
=
sinx,
π2;
π; 6) f (x)=
x
−3x
+
2
, [–10; 10]; 7) f (x)
=
sinx, ![]() π2;
π
; 8) f (x)=
π2;
π
; 8) f (x)=
![]() x2
+3x + 2
, [–15; 10].
x2
+3x + 2
, [–15; 10].
149. Funksiyani tekshiring va grafigini yasang:
3 2 x4 2
|
x |
|
|
|
1 1
|
1) ![]() y
=
3x
−
x
; 2) y =1+
x
− ; 3) y =
(x
+1)(x
−
2)
;
y
=
3x
−
x
; 2) y =1+
x
− ; 3) y =
(x
+1)(x
−
2)
;
12
![]() 4) y = x
+
4) y = x
+ ![]() ; 5) y = 6) y = x
−9
;
; 5) y = 6) y = x
−9
;
4 2

Agar nuqta harakat boshlanganidan boshlab t vaqt mobaynida s(t) masofani o‘tgan bo‘lsa, uning oniy tezligi s(t) funksiyaning hosilasiga teng ekanini bilasiz: v(t)=s'(t). Amaliyotda teskari masala: nuqtaning berilgan harakat tezligi v(t) bo‘yicha uning bosib o‘tgan yo‘li s(t) ni topish masalasi ham uchraydi. Shunday s(t) funksiyani topish kerakki, uning hosilasi v(t) bo‘lsin. Agar s'(t)=v(t) bo‘lsa, s(t) funksiya v(t) funksiyaning boshlang‘ich funksiyasi deyiladi. Umuman, shunday ta’rif kiritish mumkin:
Agar (a; b) ga tegishli ixtiyoriy x uchun F′(x)=f (x) bo‘lsa, F(x) funksiya (a; b) oraliqda f (x) ning boshlang‘ich funksiyasi deyiladi.
1-misol. a – berilgan biror son va v(t)=at bo‘lsa,
s
t(
) =
![]() at2 funksiya
at2 funksiya
at2
v(t) funksiyaning boshlang‘ichidir, chunki ss
t′(
) =
( ![]() )′
= at
=
v
t(
). 2
)′
= at
=
v
t(
). 2
2-misol. f![]() funksiya f(x)
ning
funksiya f(x)
ning
(– ∞; ∞) dagi boshlang‘ich funksiyasi bo‘ladi, chunki
F ′![]()
1 π
3-misol. f
x( )
= ![]() 2 ,
bunda x ≠
2 ,
bunda x ≠ ![]() + πk , k∈Z, funksiya uchun F(x)=tgx cos
x 2
+ πk , k∈Z, funksiya uchun F(x)=tgx cos
x 2
1 boshlang‘ich funksiya bo‘ladi, chunki (tgx)'= ![]() 2 .
2 .
cos x
1 1
4-misol. f
x( )
= ![]() , x>0, bo‘lsa, F(x)=lnx
funksiya
, x>0, bo‘lsa, F(x)=lnx
funksiya ![]() ning boshlang‘ich x x
ning boshlang‘ich x x
funksiyasi bo‘ladi,
chunki F ′(x)=(lnx)′ = ![]() 1
.
1
.
x
1 x4 x4 x4
1-masala. F1(x)
= ![]() , F 2(x) =
, F 2(x) = ![]() +17,
F 3(x) =
+17,
F 3(x) = ![]() − 25
funksiyalar ayni
− 25
funksiyalar ayni
4 4 4
bir f(x)=x3 funksiyaning boshlang‘ich funksiyalari ekanini isbotlang.
r Hosilalar jadvaliga muvofiq yoza olamiz:
1)
![]() F1′(x)
=
(
x4
)1ʹ= 4⋅
x3
=
x3
=
f
x( ).;
F1′(x)
=
(
x4
)1ʹ= 4⋅
x3
=
x3
=
f
x( ).;
4 4
2) ![]() );
);
3) F3′(x)
=
(
![]() x4
−
25)1ʹ= (
x4
−
25)1ʹ= ( ![]() x4
)′−
(25)′
= 4⋅
x4
)′−
(25)′
= 4⋅
![]() x3
– 0 = x3 = f(x).
x3
– 0 = x3 = f(x).
4 4 4 x4
Bu masaladan shunday xulosaga kelish mumkin: ixtiyoriy F(x)
= ![]() +C
+C
4
funksiya (C – biror o‘zgarmas son) ham f(x)= x3 uchun boshlang‘ich funksiya
x4 x4 x3 bo‘la oladi. Chindan ham,![]() .▲
.▲
Bu masaladan yana shunday xulosaga kelish mumkin: berilgan f(x) funksiya uchun uning boshlang‘ich funksiyasi bir qiymatli aniqlanmaydi.
Agar F(x) funksiya f(x) ning biror oraliqlari boshlang‘ich funksiyasi bo‘lsa, f(x) funksiyaning barcha boshlang‘ichlari F(x)+C (C – ixtiyoriy o‘zgarmas son) ko‘rinishida yoziladi.
F(x)+C ko‘rinishidagi barcha funksiyalar to‘plami f(x) ning aniqmas integrali deyiladi va∫ f x dx( ) kabi belgilanadi.
Demak, ∫ f x dx( ) = F x( )+C.
∫ – integral belgisi, f(x) – integral ostidagi funksiya, f (x)dx esa integral ostidagi ifoda deyiladi.
x ax
5-misol. ∫a
dx =
![]() ln a +C
, chunki hosilalar jadvaliga ko‘ra,
ln a +C
, chunki hosilalar jadvaliga ko‘ra,
ax x 1 x 1 x
( ![]() +C)′
= (a
)′⋅
+C)′
= (a
)′⋅
![]() +C′′
= a
⋅ln
a⋅
+C′′
= a
⋅ln
a⋅
![]() + 0
=
a
.
ln a ln a ln
a
+ 0
=
a
.
ln a ln a ln
a
k xk+1 xk+1 1 k+1
6-misol.
∫
x
dx =
![]() k +1
+C,
k ≠ −1, chunki (
k +1
+C,
k ≠ −1, chunki (![]() k
+1
+C)′
=
k
+1
+C)′
= ![]() k +1⋅(x )′+Cʹ=
k +1⋅(x )′+Cʹ=
k +1 k k dx
= ![]() ⋅ x
+
0
=
x
.
k = –1 bo‘lsa, x>0
da 4-misolga ko‘ra, ∫
⋅ x
+
0
=
x
.
k = –1 bo‘lsa, x>0
da 4-misolga ko‘ra, ∫ ![]() x
= ln x C+
.
k
+1
x
= ln x C+
.
k
+1
y=F(x)+C funksiyaning grafigi y=F(x) funksiya grafigini Oy o‘q bo‘ylab siljitishdan hosil qilinadi (1-rasm). O‘zgarmas son C ni tanlash hisobiga boshlang‘ich funksiya grafigining berilgan nuqta orqali o‘tishiga erishish mumkin.
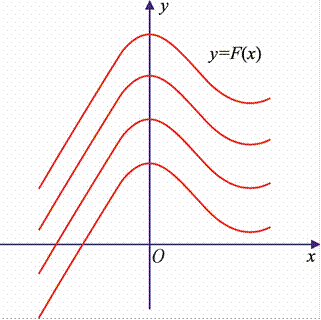
1-rasm.
2-masala. f(x)=x2 funksiyaning grafigi A(3; 10) nuqtadan o‘tadigan bosh lang‘ich funksiyasini toping.
x3
r f(x)=x2 funksiyaning barcha
boshlang‘ich funksiyalari F x( ) = ![]() +C
3
+C
3
![]() ko‘rinishda bo‘ladi, chunkiF x′ C
′ x C′ x 0 x
.
ko‘rinishda bo‘ladi, chunkiF x′ C
′ x C′ x 0 x
.
x3
O‘zgarmas
son C ni F x( ) = ![]() +C
funksiyaning grafigi (3; 10) nuq-
+C
funksiyaning grafigi (3; 10) nuq-
3
tadan o‘tadigan qilib tanlaymiz: x=3 da F(3)=10 bo‘lishi kerak. Bundan
33 x3
10
= ![]() +C
, C =1.Demak, izlanayotgan boshlang‘ich funksiya F
x( )
=
+C
, C =1.Demak, izlanayotgan boshlang‘ich funksiya F
x( )
= ![]() +1
+1
3 3
x3
bo‘ladi. Javob: +1.▲
3
![]() 3-masala.
f
x(
) =
3
x funksiyaning grafigi A(8;15)
nuqtadan o‘tadigan boshlang‘ich funksiyasini toping.
3-masala.
f
x(
) =
3
x funksiyaning grafigi A(8;15)
nuqtadan o‘tadigan boshlang‘ich funksiyasini toping.
r
![]()
![]() f
x(
) =
3
x ning barcha
boshlang‘ich funksiyalari + C ko‘ri nishida bo‘ladi, chunki
f
x(
) =
3
x ning barcha
boshlang‘ich funksiyalari + C ko‘ri nishida bo‘ladi, chunki
![]()
![]()
![]()
3 34 ′ 3 34 3
4 13
3 34 ′ 3 34 3
4 13 ![]() 13 3
13 3
![]() F
x′(
) =
⋅x +C
= (x
)′+C′
= ⋅ ⋅x +C′
= x
+0
= x.
F
x′(
) =
⋅x +C
= (x
)′+C′
= ⋅ ⋅x +C′
= x
+0
= x.
4 4 4 3
![]() 3 43
3 43
O‘zgarmas son C ni shunday tanlaymizki, F x( ) = x +C funksiyaning 4
![]() grafigi A(8,
15) nuqtadan o‘tsin, ya’ni F(8)=15 tenglik bajarilsin. x
grafigi A(8,
15) nuqtadan o‘tsin, ya’ni F(8)=15 tenglik bajarilsin. x![]() = x
x3 ekanidan15
= x
x3 ekanidan15![]() 8 8 C, bundan C=3. Demak, izlanayotgan
boshlang‘ich
8 8 C, bundan C=3. Demak, izlanayotgan
boshlang‘ich
![]()
![]()
![]()
![]() funksiya F x x x bo‘ladi. Javob: x x3+
3. ▲
funksiya F x x x bo‘ladi. Javob: x x3+
3. ▲
dx
![]() 4*-masala. ∫ x
= ln x +C ekanini ko‘rsating.
4*-masala. ∫ x
= ln x +C ekanini ko‘rsating.
r
x >
0 da ∫dxx
= lnx+C, chunki (lnx+C)′= ![]() 1x
+0=
1x
+0= ![]() 1x
;
1x
;
dx (−1) 1
![]() x < 0 da ∫
x < 0 da ∫ ![]() x
= − +ln( x) C, chunki (ln(–x)+C)′=
(−x)
+0= x . ▲
x
= − +ln( x) C, chunki (ln(–x)+C)′=
(−x)
+0= x . ▲
1. Boshlang‘ich funksiya nima? Misollar keltiring.
2. Berilgan f (x) funksiya uchun boshlang‘ich funksiya bir qiymatli topiladimi? Nima uchun?
3. Boshlang‘ich funksiya F(x) ning grafigini berilgan nuqtadan o‘tishiga qanday qilib erishish mumkin? Misolda tushuntiring.
1. Haqiqiy sonlar to‘plami R=(–∞; ∞) da f(x) funksiya uchun F(x) funksiyaning boshlang‘ich funksiya ekanini isbotlang:
|
1) F(x)=x2–sin2x+2018, |
f (x)=2x–2cos2x; |
|
x 2) F x( ) =
−cos 2 |
1 x
2 2 |
|
3) F(x)=2x4+cos2x+3x, |
f (x)=8x3–sin2x+3; |
|
4) F(x)=3x5+sin2x–7x, |
f (x)=15x4+sin2x–7. |
Quyidagi funksiyalarning barcha boshlang‘ich funksiyalarini, hosilalar jadvalidan foydalanib toping (2 – 6):
2. ![]() 1) f
x(
)=x2 ⋅ x; 2) f (x)=6x5; 3) f (x)=x10; 4) f
x(
)=
1) f
x(
)=x2 ⋅ x; 2) f (x)=6x5; 3) f (x)=x10; 4) f
x(
)= ![]()
5) f (x)=sinx; 6)
f(x)=cosx; ![]() 7) f (x)=sin2x;
7) f (x)=sin2x;
![]() 8) f (x)=cos2x;
8) f (x)=cos2x;
3. 1) f (x)=4x; 2) f(x)= πx; 3) f (x)=ex; 4) f (x)=ax;
5) f (x)=a2x; 6) f (x)=eπx; 7) f (x)=103x; 8) f (x)=e2x+3.
4. 1) f x( ) =
![]() ; 2)
f
x(
) =
; 2)
f
x(
) =
![]() ; 3)
f
x( )
=
; 3)
f
x( )
=
![]() ;
;
1 1 a
4) f
x( )
= ![]() ; 5) f
x(
) =
; 5) f
x(
) = ![]() ; 6) f x(
) =
; 6) f x(
) = ![]() .
ax ax+b ax−b
.
ax ax+b ax−b
5. 1) f (x)=sin3x; 2) f (x)=sin(2x+5); 3) f (x)=sin(4x+π);
4) f (x)=cos5x; 5) f (x)=cos(3x–2);
6) f
x( )
=
cos(2x
+
![]() ).
).
1 1 23
6. ![]()
![]() 1) f
x( )
=
x2
; 2) f x( )
=
x5
; 3) f x( )
=
(3x
+
2)
;
1) f
x( )
=
x2
; 2) f x( )
=
x5
; 3) f x( )
=
(3x
+
2)
; ![]() 4) f
x( )
=
(2x
−1)
.
4) f
x( )
=
(2x
−1)
.
7. Berilgan f (x) funksiya uchun uning ko‘rsatilgan A nuqtadan o‘tuvchi boshlang‘ich funksiyasini toping:
1) f (x)=2x+3, A(1; 5); 2) f (x)=–x2+2x+5, A(0; 2);
3) f (x)=sinx, A(0;
3); 4) f(x)=cosx, A(![]() ;
5).
;
5).
Berilgan f(x) funksiya uchun uning shunday boshlang‘ich funk- siyasini topingki, bu boshlang‘ich funksiyaning grafigi y to‘g‘ri chiziq
|
8. 1) f (x) = 4x+8, y=3; |
2) f (x)=3–x, y = 7, |
|
3) f (x)=4,5x+9, y=6,8; 9*. f (x)=ax+b, y=k. 2 |
4) f (x)=2x–6, y = 1. |
|
ax |
|
bilan faqat bitta umumiy nuqtaga ega bo‘lsin (8 – 9):
![]() Ko‘rsatma: F
x( )
= +bx
+C,
masala shartidan va
Ko‘rsatma: F
x( )
= +bx
+C,
masala shartidan va
2
2ak +b2 b2
ax2
![]() +bx
+C
=
k
+bx
+C
=
k
2
![]() kvadrat tenglamadan C ni toping. C
= =
k
+ bo‘ladi.
kvadrat tenglamadan C ni toping. C
= =
k
+ bo‘ladi.
2a 2a
10*. f(x) uchun uning shunday boshlang‘ich funksiyasini topingki, bu boshlang‘ich funksiyaning grafigi ko‘rsatilgan nuqtalardan o‘tsin:
16
1) ![]() f
x′( )
=
3
, A (1; 10) va B (4;
–2); x
f
x′( )
=
3
, A (1; 10) va B (4;
–2); x
54
2) ![]() f
x′( )
= 4
, A(–1; 4) va B (3;
4); x
f
x′( )
= 4
, A(–1; 4) va B (3;
4); x
3) f ′(x)=6x, A(1;6) va B(3;30); 4) f ′(x) = 20x3; A(1;9) va B(–1;7).
Ko‘rsatma: Berilgan f ′(x) bo‘yicha f(x)+C[1] topiladi. So‘ngra f(x)+C1 uchun boshlang‘ich funksiyasi F x( ) = ∫ f x dx( ) +C x1 +C2 topiladi. Berilgan nuqtalar koordinatalarini oxirgi tenglikka qo‘yib, C1 va C2 sonlarni topish uchun chiziqli tenglamalar sistemasiga kelinadi.
![]()
![]() 11*. Berilgan f (x)
funksiya uchun uning shunday boshlang‘ich funks iyasini topingki, bu
boshlang‘ich funksiyaning grafigi bilan f (x) hosila sining
grafigi abssissasi ko‘rsatilgan nuqtada kesishsin:
11*. Berilgan f (x)
funksiya uchun uning shunday boshlang‘ich funks iyasini topingki, bu
boshlang‘ich funksiyaning grafigi bilan f (x) hosila sining
grafigi abssissasi ko‘rsatilgan nuqtada kesishsin:
1) f x( ) = (3x− 2), x0 =1; 2) f x( ) = (4x+5), x0 = −1;
12.Berilgan f(x) funksiya uchun ko‘rsatilgan nuqtadan o‘tuvchi boshlang‘ich funksiyani toping:
5 3
1)
f x( ) =
![]() , A(3; 7); 2) f x(
) =
, A(3; 7); 2) f x(
) =
![]() , A(0;
1); x
−
2 x +[2]
, A(0;
1); x
−
2 x +[2]
![]() 3) f x( ) =
cos
x, A(;
8); 4) f x(
) =
sin
x, A(π;
1 0).
3) f x( ) =
cos
x, A(;
8); 4) f x(
) =
sin
x, A(π;
1 0).
13.F(x) funksiya son o‘qida f (x) funksiyaning boshlang‘ich funksiyasi ekanini ko‘rsating:
x x
![]()
1) F x( ) = k e⋅ k , f x( ) = ek , k ≠ 0;
2) F(x)=C+sinkx, f(x)=k∙coskx, C – o‘zgarmas son;
3) F(x)=C+coskx, f(x)=–k∙sinkx, C – o‘zgarmas son;
4)
![]() ( ) sin(5 12), f
x( )
=
cos(5x
+12).
( ) sin(5 12), f
x( )
=
cos(5x
+12).
14.f (x) funksiyaning ko‘rsatilgan nuqtadan o‘tuvchi boshlang‘ich funksiyasini toping:
|
1) f (x) = 3x2; |
|
2 2 ; 4log2 x − log2 y = 2 |
|
2) f (x)=4x[3][4]; |
|
5x + 5y = 30, x y 3 5⋅ − 2 5⋅ =[5]; |
|
3) f (x)=cosx; |
|
3π x
+
y
= 2 4x −3y = −π; |
|
1 |
|
2x + 3y = 4, x y 3 2⋅ − 3 = 0. |
|
4) f x( ) = 5x + e; |
||

Integrallar jadvalini hosilalar jadvali yordamida tuzish mumkin.
|
№ |
Funksiya f(x) |
Boshlang‘ich funksiya F(x)+C |
|
1 |
xp, p ≠–1 |
x p+1
|
|
2 |
1/x |
nl׀x׀+C |
|
3 |
ex |
ex+C |
|
4 |
sin x |
–cos x+C |
|
5 |
cos x |
sin x+C |
|
6 |
(kx b+ )p, p ≠ −1, k ≠ 0
|
(kx +b)p+1
|
|
7 |
1
kx b+ |
1
|
|
8 |
ekx+b, k ≠ 0 |
1 kx b+ k |
|
9 |
sin(kx +b), k ≠ 0 |
1 − |
|
10 |
cos(kx +b), k ≠ 0 |
1
|
|
11 |
1/cos2x |
tgx + C |
|
12 |
1/sin2x |
– ctgx+C |
|
13 |
ax |
ax
ln a |
|
14 |
|
arctgx + C |
|
15 |
f(kx+b) |
1
|
|
16 |
f(g(x))g |
F(g(x))+C |
Biror X oraliqda aniqlangan F(x) funksiya f(x) funksiyaning boshlang‘ich funksiyasi bo‘lishi uchun ikkala F(x) va f (x) funksiya ham ayni shu X oraliqda aniqlangan bo‘lishi kerak.
Masalan, ![]() funksiyaning 5x–8>0, ya’ni x >1,6
oraliqdagi integrali, jadvalga muvofiq,
funksiyaning 5x–8>0, ya’ni x >1,6
oraliqdagi integrali, jadvalga muvofiq, ![]() ln(5
–8)x +С ga teng.
ln(5
–8)x +С ga teng.
Differensiyalash qoidalaridan foydalanib, integrallash qoidalarini bayon qilish mumkin.
F(x) va G(x) funksiyalar biror oraliqda, mos ravishda, f(x) va g(x) funksiyalarning boshlang‘ich funksiyalari bo‘lsin. Ushbu qoidalar o‘rinlidir:
1-qoida: a∙F(x) funksiya a∙f (x) funksiyaning boshlang‘ich funksiyasi bo‘ladi, ya’ni
∫a f x dx⋅ ( ) = a F x⋅ ( )+C.
2-qoida: F(x)±G(x) funksiya f(x)±g(x) funksiyaning boshlang‘ich funksiyasi bo‘ladi, ya’ni:
∫(f(x) ± g(x))dx=∫ f (x)dx ± ∫g(x)dx =F(x) ± G(x)+C.
1-misol. f (x)=5sin(3x+2) funksiyaning integralini toping.
r Bu funksiyaning integralini 1-qoida va integrallar jadvalining9-bandiga muvofiq topamiz:
∫ f x dx( ) = ∫ 5sin(3x + 2)dx = 5∫ sin(3x + 2)dx =
![]() 5
( cos(3x 2)) C cos(3x 2) C,
5
( cos(3x 2)) C cos(3x 2) C,
chunki integrallar jadvaliga ko‘ra
![]() sin(3 2) cos(3 2) .
sin(3 2) cos(3 2) .
Javob: −![]() cos(3x + 2) +C.▲
cos(3x + 2) +C.▲
2-misol. f (x)=8x7+2cos2x funksiyaning integralini toping.
r Bu funksiyaning integralini 1- va 2-qoidalar hamda integrallar jadvalining 1- va 10-bandiga muvofiq topamiz:
∫ f x dx( ) = ∫ (8x7 + 2cos2x)dx== 8∫ x dx7 + 2∫cos2xdx
![]() .
.
Javob: x8 + sin 2x +C. ▲
xdx
3-misol. ∫ ![]() x2 +
8 integralni
hisoblang.
x2 +
8 integralni
hisoblang.
r Bu kabi misollarni yechishda o‘zgaruvchini almashtirish qulay.
![]() Agar x2+8=u deyilsa, du = 2xdx, xdx
=4du bo‘ladi. U holda
Agar x2+8=u deyilsa, du = 2xdx, xdx
=4du bo‘ladi. U holda
![]() ׀u׀ + C =
׀u׀ + C = ![]() ln(x2
+
8)
+C.
ln(x2
+
8)
+C.
Tekshirish: Topilgan boshlang‘ich funksiyadan hosila olinsa, integral
x ostidagi funksiya ![]() 2 hosil bo‘lishi kerak. Chindan ham,
2 hosil bo‘lishi kerak. Chindan ham,
x + 8
![]()
![]()
![]()
1
ln(x2 +8)+C′
= 1
(ln(x2 +8))′+C′
= 1
1
ln(x2 +8)+C′
= 1
(ln(x2 +8))′+C′
= 1·
21 ·(x2+8)ʹ= 1· 22x
=
2x
.
2 2 2 x +8 2 x +8 x +8
![]() Javob: ln( 8) .
▲
Javob: ln( 8) .
▲
4-misol. ∫esinx cos xdx integralni hisoblang.
r sinx=t almashtirish bajaramiz. U holda dt = cosxdx va berilgan integ ral ∫e dtt ko‘rinishni oladi. Integrallar jadvallarining 3-bandiga ko‘ra
∫e dtt = et +C bo‘ladi. Demak, ∫esinx cos xdx = essinx+C.
Tekshirish. (esinx+C)′ = (esinx)′+C′=esinx(sinx)'+0=esinx cosx – berilgan in teg ral ostidagi funksiyani hosil qildik.
Javob: esinx + C. ▲
5-misol. ∫sin5x⋅cos3xdx integralni hisoblang.
r Bunda 2sin5x · cos3x = sin8x+sin2x ayniyat yordam beradi. U holda
![]()
![]() .
.
cos8x cos 2x
![]() Javob: − − +C. ▲
Javob: − − +C. ▲
16 4
6*-misol. ∫cosmx cosnxdx integralni hisoblang.
r
![]() +cos(m–n)x)
ayniyatga va integrallash
+cos(m–n)x)
ayniyatga va integrallash
jadvalining 10-bandiga muvofiq:
![]()
1 sin(m+ n x) 1 sin(m−n x)
![]() = ⋅ + ⋅ +C.
= ⋅ + ⋅ +C.
2 m+ n 2 m−n
2
1 sin(m+ n x) 1 sin(m−n x)
![]() Javob: ⋅
+ ⋅ +C. ▲ 2 m+ n
2
m−n
Javob: ⋅
+ ⋅ +C. ▲ 2 m+ n
2
m−n
dx
7-misol. ∫![]() x2 −
5x + 6 integralni hisoblang.
x2 −
5x + 6 integralni hisoblang.
r Integral ostidagi funksiya uchun quyidagi tengliklar o‘rinlidir:
1 1 ( 2) ( 3)x − − x − 1 1
2
![]() = = = − . x −5
6 ( 2)( 3)x + x
− x
− (
2)( 3)x − x
− x
−3
x −2
= = = − . x −5
6 ( 2)( 3)x + x
− x
− (
2)( 3)x − x
− x
−3
x −2
Bundan
dx 1 1 dx dx
![]() ∫
x2 −
5x
+
6
=
∫
(
x − 3 −
x
−
2)dx
=
∫
x
−
3
−
∫
x
−
2
=
∫
x2 −
5x
+
6
=
∫
(
x − 3 −
x
−
2)dx
=
∫
x
−
3
−
∫
x
−
2
=
![]() x −
3
nl=׀x–3׀–ln׀x–2׀+C = ln +C,
x − 2
x −
3
nl=׀x–3׀–ln׀x–2׀+C = ln +C,
x − 2
Javob:ln│ ![]() x
− 3│+C. ▲ x
−
2
x
− 3│+C. ▲ x
−
2
dx
8-misol. ∫
1![]() + cos
x integralni hisoblang.
+ cos
x integralni hisoblang.
r Bu integralni hisoblash uchun 1+cosx=2cos
2
![]() ekanidan foydalanamiz. U holda 2 x va ∫
cosdx2 x
= tgx+C
ekanidan foydalanamiz. U holda 2 x va ∫
cosdx2 x
= tgx+C
dx dx 1 x x
![]() ∫1+cos
x =∫ 2 x
=
2·2·tg
∫1+cos
x =∫ 2 x
=
2·2·tg
![]() 2 +C =tg
2 +C =tg ![]() 2
+C.
2
+C.
2cos
2
x x 1 x 1 1 1
Tekshirish:
![]() 2 2 2 2 2 2 1+
cos
2 2 2 2 2 2 1+
cos
cos cos
integral ostidagi funksiya hosil bo‘ldi.
x
Javob: tg![]() . ▲
. ▲
9-misol. ∫sin 22 xdxintegralni hisoblang.
r Integralni hisoblash uchun 2sin 22x=1– cos4x ayniyatdan foyda- lanamiz.
![]() sin4 .
sin4 .
x 1
![]() Javob: 2 − 8
sin 4x C+ . ▲
Javob: 2 − 8
sin 4x C+ . ▲
1. Integrallar jadvalidagi o‘zingiz xohlagan 4 ta misolni tanlang va uni isbotlang.
2. Integrallashning sodda qoidalarini bayon qiling. Misollarda tushuntiring.
3. O‘zgaruvchi almashtirish usuli nima? ∫ecos2x sin2xdx integralni hisoblashda shu usulni qo‘llang va misolni yechish jarayonini tushuntiring.
Berilgan funksiyaning boshlang‘ich funksiyalaridan birini toping (16 – 18):
![]() 5 3 7 4 4 4 5 3
5 3 7 4 4 4 5 3
![]()
![]() 16. 1) 3x
−
4x
; 2) 8x −
5x
; ; 4)
4
+
5
;
x x 5) 3 x +
33 x; 7) 5x4 +
4x3 −
2x2.
16. 1) 3x
−
4x
; 2) 8x −
5x
; ; 4)
4
+
5
;
x x 5) 3 x +
33 x; 7) 5x4 +
4x3 −
2x2.
|
17. 1) 5cos x − 3sin x; |
|
2) 7sin x + 4cos ;x |
|
3) 2cos x a− x; |
|
4) 5ex+2cosx+1 |
|
5) 4+2·e–x–7sinx; |
|
6 4 6) −x |
![]() ; 3 x
+
x
−e
.
; 3 x
+
x
−e
.
1 6
![]() 18. 1) (x
−
2)3; 2) (x +
5)4; 3) x −
5 4)
3 ;
18. 1) (x
−
2)3; 2) (x +
5)4; 3) x −
5 4)
3 ;
![]() 84 4
84 4
![]() 5) 4cos(x+
+5)
5) 4cos(x+
+5) ![]() ; 6) 2sin(x−
−3) ; 7) (3x + 7)
+
5
.
x−7x−2 x
; 6) 2sin(x−
−3) ; 7) (3x + 7)
+
5
.
x−7x−2 x
Berilgan funksiyaning barcha boshlang‘ich funksiyalarini toping (19 – 20):
2x
|
19. 1) cos(5x + 3); |
2) sin(7x −
6); 3) cos( |
|
5x 4) sin( 7 |
5) e
|
|
4 7) |
3 5 8) cos 4x sin 5x |
4 3 4 1 2
20. ![]() 1)
1) ![]() 5 −
(1−
2
)x ; 2) (3x
+
2)
−
5 −
(1−
2
)x ; 2) (3x
+
2)
−
![]() 6 ; 3) x + −1;
x x
6 ; 3) x + −1;
x x
3 1
4)
2x
−
![]() sin2
x + 6; 5) (1+
3
)(x x −1); 6)
sin2
x + 6; 5) (1+
3
)(x x −1); 6)
21. Berilgan f (x) funksiya uchun grafigi A(x; y) nuqtadan o‘tadigan boshlang‘ich funksiyani toping:
![]()
![]() 1) f x( ) =
sin
4 ,x A(; 7); 2) f (x)=cos5x, A(;
4);
1) f x( ) =
sin
4 ,x A(; 7); 2) f (x)=cos5x, A(;
4);
2 2 3 1
![]()
![]() 3) f
x(
) =
3x
+,
A(−1;0); 4) f x( )=4x
−
2
x−1 A(2;0) ; x + 2
3) f
x(
) =
3x
+,
A(−1;0); 4) f x( )=4x
−
2
x−1 A(2;0) ; x + 2
5)
![]()
![]() f x( ) =
cos2
3x
+
sin2
3x
+sin
4 ,x A( ; );
f x( ) =
cos2
3x
+
sin2
3x
+sin
4 ,x A( ; );
x
6)
![]() f (x) = tgx·ctgxx
−
2cos ,
A(2π; 2 );π
f (x) = tgx·ctgxx
−
2cos ,
A(2π; 2 );π
![]() f
x( ) = 2 +
4x, A2(2;6); 8) f x( ) =
6x2 − 1 ., A(–2; 4).
f
x( ) = 2 +
4x, A2(2;6); 8) f x( ) =
6x2 − 1 ., A(–2; 4).
7)
|
Integrallarni toping (22 – 28): |
|
|
|
22. 1) ∫(x3 −sin2x −3)dx; |
|
2) ∫(x4 +cos3x + 4)dx; |
|
x x
|
|
x x
|
|
|
|
2) |
![]() 5
−
2x 2 2
−
x
5
−
2x 2 2
−
x
sin x cos x
3)∫sin2 cos2x xdx; 4)∫(sin3 cosx x +cos3 sin )x x dx;
5)∫(sin2x⋅sin4x +cos2 cos )x x dx; 6) ∫cos 52 xdx.
24*. 1)∫sin5 cos3x xdx; 2) ∫cos2 cos3x xdx; 3) ∫sin7 sin3x xdx.
![]()
![]()
![]() xdx
xdx
![]()
![]() 25*. 1)∫
25*. 1)∫
![]() x +1
dx; 2)
∫
x2 −
7x +12
; 3) .
x +1
dx; 2)
∫
x2 −
7x +12
; 3) .
x5 + x3 − 2 x2 −1
|
dx 4) 1− cos 2x |
5) ∫ 4(x2 −4) ; |
6) ∫(1−2sin2 5 )x dx.
|
|
27. 1)∫(x3 −1)4 x dx2 ; |
xdx 2) ∫ (1+ x2 3) ; |
tgx
3) ∫ cos3 x dx; |
|
ctgx 4)∫ |
5) ∫sin3 xdx;
|
∫cos3 xdx. 6) |
26. 1)∫ x2 +1 dx; 2) x2 +1 dx; 3) ∫ 1+ cos 2x ; dx
xdx(x −1)dx
|
|
|
|
4) ∫(tg2x+tg4x)dx;
|
5) ∫(ctg2x+ctg4x dx) . |
![]() 28*. 1) ∫ ; 2) ∫ x⋅ x
−4ddx; 3) ∫ ;
28*. 1) ∫ ; 2) ∫ x⋅ x
−4ddx; 3) ∫ ;
Berilgan f (x) funksiya uchun grafigi A(x; y) nuqtadan o‘tadigan boshlang‘ich funksiyani toping (29 – 30):
3 x
29. ![]()
![]() 1) f x( ) = ⋅cos , A(π; 4);
1) f x( ) = ⋅cos , A(π; 4);
![]() 2 3
2 3
2) f x x, A(; 3);
x π
3)
![]()
![]() f x( ) =
2sin
5x + 2cos , A( ; 0);
f x( ) =
2sin
5x + 2cos , A( ; 0);
2 3
30. 1) f(x)=3x2–2x+8, A(1; 9); 2) f x( ) = 4x3 − 3x2 + 2x +1, A(–1; 4);
3) f x( ) = 5x4 + 3x2 + 2 , A(–2; 1).
31. Integralni toping:
![]() 1) ∫(x2 −1)(x
+
2)dx; 2) ∫(x
+
2)(x2 −9)dx; 3)∫(x2 +1)(x3 −1)dx;
1) ∫(x2 −1)(x
+
2)dx; 2) ∫(x
+
2)(x2 −9)dx; 3)∫(x2 +1)(x3 −1)dx;
![]() 1−4x2
+ 1−2x 9x2
−4− 3x
+2
1−4x2
+ 1−2x 9x2
−4− 3x
+2
4) ∫ 1−2x dx; 5) ∫ 3x + 2 d dx;
6) ∫(e5 2− x − 2 )x dx; 7) ∫(e3x+2 +10 )x dx.
32. Integralni hisoblang:
1) ∫ x2 + 66xx +10 ; 2) ∫ x2 − 4x + 5 ; 3) ∫ x2 +10x + 26 .
dx
![]()
![]() N a m u n a : I
=
∫
x2 +
4x + 5 integralni hisoblang.
N a m u n a : I
=
∫
x2 +
4x + 5 integralni hisoblang.
![]() r I ∫ ∫ ;
x+2 = u deyilsa, 1+(x+2)2=1+u2
r I ∫ ∫ ;
x+2 = u deyilsa, 1+(x+2)2=1+u2
x′=u′ va integrallar jadvalining 14–15 bandlariga ko‘ra du
![]()
![]() I
=
∫ 2 =
arctgu
+C
=
arctg(x
+
2)+C.
I
=
∫ 2 =
arctgu
+C
=
arctg(x
+
2)+C.
1+u
Tekshirish:
(arctg(x+2)+C)′=(arctg(x+2))′ +C ′ =+ 0 =
1 1
![]() = 2 = 2 .
= 2 = 2 .
1+ (x + 2) x + 4x + 5
Javob: arctg(x+2)+C.▲
Integrallash qoidalaridan yana biri bo‘laklab integrallashdir.
3-qoida*. Agar biror X oraliqda
f (x) va g(x) funksiyalar uzluksiz f (x)
va g'(x) hosilaga ega bo‘lsa, u holda
∫ f x g x dx( ) '( ) = f x g x( ) ( ) − ∫ g x f( ) '( )x dx (1)
formula o‘rinlidir. Bu formula bo‘laklab integrallash formulasi deyiladi.
Bu formulaning isboti f (x) va g(x) funksiyalar ko‘paytmasini differen-
siallash qoidasi (f(x)g(x))=f (x)g(x)+f(x)g(x) va ∫ f (x)dx=f(x)+C ekani dan kelib chiqadi.
Formuladan foydalanish
yo‘rig‘i: 1) integral ostidagi ifoda f(x) va g![]() (x) lar ko‘paytmasi ko‘rinishida yozib olinadi; 2) g (x)
va g(x)f (x) ifodalarning integrallarini oson
(qulay) hisoblanadigan qilib olish nazarda tutiladi.
(x) lar ko‘paytmasi ko‘rinishida yozib olinadi; 2) g (x)
va g(x)f (x) ifodalarning integrallarini oson
(qulay) hisoblanadigan qilib olish nazarda tutiladi.
1-misol. ∫ x e dx⋅ x integralni hisoblang.
r Bu yerda f(x)=x, g (x)=ex deb olish qulay, chunki g x(
) =
∫ g x dx'( ) =
∫e dxx =
ex
, f ![]() (x)=1. U holda (1) ga
asosan,
(x)=1. U holda (1) ga
asosan,
∫ xe dxx = x e⋅ x − ∫e dxx = x e⋅ x −ex +C.
Demak, ∫ xe dxx = ex ⋅(x −1)+C.
Javob: ex(x–1)+C. ▲
2-misol. ∫ln xdx integralni hisoblang.
∆ Integral ostidagi lnx funksiyani f(x)=lnx
va g![]() (x)=1 larning
ko‘paytmasi deb hisoblaymiz: lnx=f (x) · g
(x)=1 larning
ko‘paytmasi deb hisoblaymiz: lnx=f (x) · g![]() (x).
(x).
1
![]() U holda f
(x)
= ,
g x( ) = ∫1⋅dx
=
x
+
C.
x
U holda f
(x)
= ,
g x( ) = ∫1⋅dx
=
x
+
C.
x
(1) formulaga ko‘ra,
1
∫ln
xdx = xln
x − ∫ x⋅
![]() x dx =
xln
x − ∫dx
=
xln
x − x +C
=
x dx =
xln
x − ∫dx
=
xln
x − x +C
=
x
=
x(ln
x −1)+C
=
x⋅(ln
x −ln )e +C
=
x⋅ln ![]() +C.
+C.
e
x Demak,∫ ln
xdx x= ⋅ln ![]() e
+C.
e
+C.
Tekshirish:
x x x x
(xln ![]() +C)′
= (xln
+C)′
= (xln
![]() )′+C′
= x′⋅ln
)′+C′
= x′⋅ln
![]() + x(ln
+ x(ln
![]() )′+ 0
=
e
e e e xe1
)′+ 0
=
e
e e e xe1
=
ln ![]() + x·
+ x·![]() ·
·
·
·![]() ·=lnx–lne+1=lnx–1+1=lnx.
exe
x
·=lnx–lne+1=lnx–1+1=lnx.
exe
x
Javob: x⋅ln ![]() +C.
▲ e
+C.
▲ e
3-misol. ∫ xcos xdxintegralni hisoblang.
r Integralni hisoblash uchun f (x)=x, g ′ (x)=cosx deyish qulay. U holda f ′ (x) =1, g x( ) = ∫cos xdx = sin x (bu yerda boshlang‘ich funksiya- lardan bittasini old ik, shuning uchun o‘zgarmas son C ni yozmad ik). Bo‘laklab integrallash formulasiga muvofiq,
∫ xcos xdx = x⋅sin x − ∫sin xdx = xsin x +cos x +C.
Javob: x sinx+cosx+C. ▲
Integrallarni hisoblang (33 – 35):
![]() 33*. 1)∫ xsin
xdx; 2) ∫x2cosxdx; 3) ∫ xln
xdx; 4) ∫ 2xln
xdx.
33*. 1)∫ xsin
xdx; 2) ∫x2cosxdx; 3) ∫ xln
xdx; 4) ∫ 2xln
xdx.
xx
![]()
![]() 34*. 1)∫ xcos2xdx; 2) ∫ xsin3xdx; 3) ∫xsin
34*. 1)∫ xcos2xdx; 2) ∫ xsin3xdx; 3) ∫xsin
![]() 3 dx; 4) ∫x
cos
3 dx; 4) ∫x
cos
![]() 4 dx.
4 dx.
35*. 1) ∫a2x∙xdx; 2) ∫ 3x∙xdx; 3) ∫ 5x∙xdx; 4) ∫tg2nxdx;
2x+1 −5x−1 e3x +1 x x 2
|
5) ∫ 10x ; |
6) ∫ ex +1 dx; |
7) ∫ ; |
|
8) ∫(e–x + e–2x )dx ; |
e4x −1 9) ∫
|
e dxx 10) ∫ |
|
11) ∫ x e⋅ −x2dx ; |
dx 12) ∫
|
ln2 x
|
dx(3 + 4 ) dx
2-rasmda tasvirlangan shakl egri chiziqli trapetsiya deyiladi. Bu shakl yuqoridan y = f (x) funksiyaning grafigi bilan, quyidan [a, b] kesma bilan, yon tomonlardan esa x=a, x=b to‘g‘ri chiziqlarning kesmalari bilan chegaralangan. [a; b] kesma egri chiziqli trepetsiyaning asosi deyiladi.
Egri chiziqli trapetsiyaning yuzini qaysi formulaga ko‘ra hisoblaymiz, degan savol tug‘iladi.
Bu yuzni S deb belgilaylik. S yuzni f (x) funksiyaning boshlang‘ich funksiyasi yordamida hisoblash mumkin ekan. Shunga oid mulohazalarni keltiramiz.
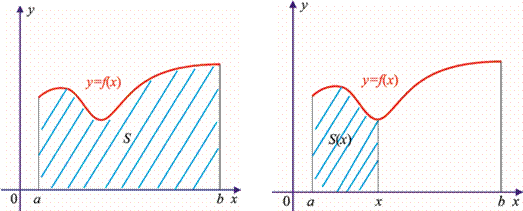
2-rasm. 3-rasm.
[a; x] asosli egri chiziqli trapetsiyaning yuzini S(x) deb belgilay- miz (3-rasm), bunda x shu [a; b] kesmadagi istalgan nuqta: x=a bo‘l- ganda [a; x] kesma nuqtaga aylanadi, shuning uchun S(a)=0; x=b da S(b) = S.
S (x) ni f (x) funksiyaning boshlang‘ich funksiyasi bo‘lishini, ya’ni S ′(x) = f (x) ekanini ko‘rsatamiz.
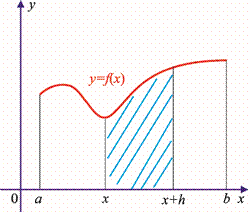
4-rasm.
r S(x+h) – S(x) ayirmani ko‘raylik, bunda h>0 (h<0 hol ham xud di shunday ko‘riladi). Bu ayirma asosi [x; x+h] bo‘lgan egri chiziqli trapetsiyan ing yuziga teng (4-rasm). Agar h son kichik bo‘lsa, u holda bu yuz taqriban f (x) ·h ga teng, ya’ni S(x+h) – S(x) ≈ f (x) ·h. Demak,
S x h S x( + ) − ( )
![]() ≈ f
x( ).
≈ f
x( ).
h
Bu taqribiy tenglikning chap qismi h→0 da hosilaning ta‘rifiga ko‘ra S′(x) ga intiladi. Shuning uchun h→0 da S ′(x)=f(x) tenglik hosil bo‘ladi. Demak, S(x) yuz f (x) funksiya uchun boshlang‘ich funksiyasi ekan.▲
Boshlang‘ich funksiya S(x) dan ixtiyoriy boshqa boshlang‘ich F(x) funksiya o‘zgar mas songa farq qiladi, ya’ni
F(x)=S(x)+C.
Bu tenglikdan x=a da F(a) = S(a)+C va S(a) = 0 bo‘lgani uchun C=F(a). U holda (1) tenglikni quyidagicha yozish mumkin:
S(x)=F(x)–F(a). Bundan x=b da S(b)=F(b)–F(a) ekanini topamiz.
|
Demak, egri chiziqli trapetsiyaning yuzini (2-rasm) quyidagi formula yordamida hisoblash mumkin: S=F(b)–F(a), (2) bunda F(x) – berilgan f (x) funksiyaning istalgan boshlang‘ich funk- |
siyasi.
Shunday qilib, egri chiziqli trapetsiyaning yuzini hisoblash f(x) funksiyaning F(x) boshlang‘ich funksiyasini topishga, ya’ni f(x) funksiyani integrallashga keltiriladi.
|
F(b) – F(a) ayirma f (x) funksiyaning [a; b] kesmadagi aniq integrali b deyiladi va bunday belgilanadi: ∫ f x dx( ) a (o‘qilishi: “a dan b gacha integral ef iks de iks“), ya’ni b ∫ f x dx( ) = F b( )− F a( ). (3) a (3) formula Nyuton–Leybnis formulasi deb ataladi. (2) va (3) formulaga muvofiq: b S = ∫ f x dx( ) . (4) a Integralni hisoblashda, odatda, quyidagicha belgilash kiritiladi:
F(b)–F(a)=F(x). U holda (3) formulani shunday yozish mumkin: a
S = ∫a f x dx( ) = F(x)a. (5) |
Shu o‘rinda qisqacha tarixiy ma’lumotni aytish joiz.
Egri chiziqlar bilan chegaralangan shakl yuzini hisoblash masalasi aniq integral tushunchasiga olib kelgan. Uzluksiz f (x) funksiya
aniqlangan [a; b] kesma a=x0, x1.., xn–1, ... xn= b nuqtalar yordamida o‘zaro teng [xk; xk+1] (k=0, 1, ... n–1) kesmalarga bo‘lingan va har bir [xk; xk+1] kesmadan ixtiyoriy ξk nuqta olingan. [xk; xk+1] kesma uzunligi Δxk=xk+1–xk ni berilgan f (x) funksiyaning ξk nuqtadagi qiymati f (ξk) ga ko‘paytirilgan va ushbu
S n=f (ξ 0)Δx 0+f (ξ 1)Δx 1+...+f (ξ k–1)Δ n–1 (6)
yig‘indisi tuzilgan, bunda har bir qo‘shiluvchi asosi Δxk va balandligi f (ξk) bo‘lgan to‘g‘ri to‘rtburchakning yuzidir. Sn yig‘indi egri chiziqli trapetsiyaning yuzi S ga taqriban teng: Sn≈S (5-rasm).
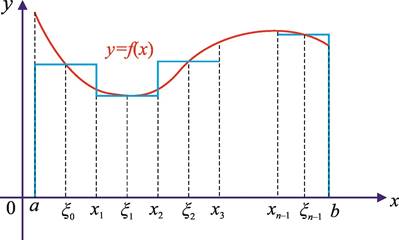
5-rasm.
(6) yig‘indi f (x) funksiyaning [a; b] kesmadagi integral yig‘indisi deyiladi. Agar n cheksizlikka intilganda (n→∞), Δxk nolga intilsa (Δxk→0), u holda Sn integral yig‘indi biror songa intiladi. Ayni shu son f (x) funksiyaning [a; b] kesmadagi integrali deb ataladi.
1-misol. 6-rasmda tasvirlangan egri chiziqli trapetsiyaning yuzini toping.
4
r (4) formulaga muvofiq S = ∫x dx2 . Bu integralni Nyuton–Leybnis
1
formulasi (3) yordamida hisoblaymiz. f (x)=x2 funksiyaning bosh- 3 x
lan g‘ich funksiyalaridan biri F x(
) = ![]() ekani ravshan. Demak,
ekani ravshan. Demak,
3
4 2 x3 4 1 3 3 1
![]() S
=
∫1 x
dx =
3
1 =
3(4
−1
) =
S
=
∫1 x
dx =
3
1 =
3(4
−1
) =
![]() 3⋅63
21= (kv. birlik).
3⋅63
21= (kv. birlik).
Javob: S = 21 kv. birlik. ▲
2-misol. 7-rasmdagi shtrixlangan soha yuzini toping.
r Shtrixlangan soha egri chiziqli trapetsiya bo‘lib, u yuqoridan y=cosx
π π
![]() funksiyaning
grafigi, pastdan esa −
2
2;
kesma bilan chegaralangan. y=cosx – juft funksiya, soha Oy o‘qqa nisbatan simmetrik. Shu ma'lumotlarga
funksiyaning
grafigi, pastdan esa −
2
2;
kesma bilan chegaralangan. y=cosx – juft funksiya, soha Oy o‘qqa nisbatan simmetrik. Shu ma'lumotlarga
π
![]() ko‘ra, soha yuzi
ko‘ra, soha yuzi ![]() xdx yuzining ikki barobariga teng deyish mumkin.
xdx yuzining ikki barobariga teng deyish mumkin.
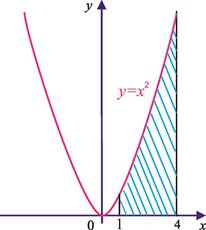
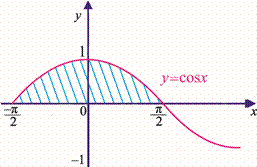
6-rasm. 7-rasm.
Nyuton–Leybnis formulasi va (5) formulaga ko‘ra:
![]() πp2 =
sinπp −sin(−πp) = − −1 (
1) =
+ =1
1 2 (kv. birlik).
πp2 =
sinπp −sin(−πp) = − −1 (
1) =
+ =1
1 2 (kv. birlik).
![]()
![]() ∆S
= cos
xdx = sinx–πp
∆S
= cos
xdx = sinx–πp
2 2 2
Javob. 2 kv.birlik. ▲
3-misol. ![]() xdx aniq integralni hisoblang.
xdx aniq integralni hisoblang.
r Nyuton–Leybnis formulasi va (5) formulasiga ko‘ra:
πp
π
∆∫cos
xdx = sin x ![]() π0 = sinπp −sin0 =
0.
π0 = sinπp −sin0 =
0.
0
Javob: 0. ▲
4-misol. ![]() x x dx
aniq integralni hisoblang.
x x dx
aniq integralni hisoblang.
r Nyuton–Leybnis formulasi va (5) formulaga ko‘ra:
2
2 2 3 3 2 2 22 37 81
![]()
![]() −∫1(2x
−3x
+
4)dx
=
(3
x − 2 x +
4
)x −1
=
3
−
−( 6
) =
6
=13,5.(kv. birlik).
−∫1(2x
−3x
+
4)dx
=
(3
x − 2 x +
4
)x −1
=
3
−
−( 6
) =
6
=13,5.(kv. birlik).
Javob: 13,5 kv. birlik. ▲
5-misol. S 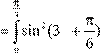 x dx aniq integralni hisoblang.
x dx aniq integralni hisoblang.
r Avval aniqmas integralni topamiz:
![]()
![]()
![]()
![]() U holda S
=
1
(x − 1 sin(6x +πp )) πp3 = 1·(πp −
U holda S
=
1
(x − 1 sin(6x +πp )) πp3 = 1·(πp − ![]() 1sin(2πp+πp))−
1
(0−
1sinπp) =
1sin(2πp+πp))−
1
(0−
1sinπp) =
2 6 3 0 2 3 6 3 2 6 3
![]() sin sin .
sin sin .
Javob: S ![]() . ▲
. ▲
6-misol. ![]() dx aniq
integralni hisoblang.
dx aniq
integralni hisoblang.
r Avval aniqmas integralni topamiz:
![]() Integrallar
jadvaliga ko‘ra ∫ 2x
−
3dx
=
3
⋅(2x
−
3)
+C. U holda
Integrallar
jadvaliga ko‘ra ∫ 2x
−
3dx
=
3
⋅(2x
−
3)
+C. U holda
![]()
1 2 = ⋅(2 6⋅ − 3)
![]()
![]()
![]()
![]() ∫62 2x
−
3dx
=
3
⋅(2x
−
3)3
16 13
23
−
(2
2⋅ −
3)23
= 13
⋅(27
−1)
=
263
=
8
32
.
∫62 2x
−
3dx
=
3
⋅(2x
−
3)3
16 13
23
−
(2
2⋅ −
3)23
= 13
⋅(27
−1)
=
263
=
8
32
.
Javob: 8 ![]() .
▲
.
▲
Aniq integral quyidagi xossalarga ega:
a a
1. ∫ f x dx( ) = 0. Chindan ham, ∫ f x dx( ) = F a( )− F a( ) = 0.
a a
b a
2∆. ∫ f x dx( ) = −∫ f x dx( ) .
a b
b a
Δ∆∫ f x dx( ) = F b( )− F a( ); ∫ f x dx( ) = F a( )− F b( ) = −(F b( )− F a( ) .)
a b
a b
Demak, −∫ f x dx( ) = F b( )− F a( ) = ∫ f x dx( ) .▲
b a
a c b
3. a, b, c – haqiqiy sonlar bo‘lsa, ∫ f x dx( ) = ∫ f x dx( ) + ∫ f x dx( ) . (aniq
integralning additivlik xossasi). b a c
a a
4. f x( ), x∈R, juft funksiya bo‘lsa, u holda ∫ f x dx( ) = 2⋅∫ f x dx( ) .
−a 0 b
5. Agar f x( ) ≥ 0, x∈[a b, ] bo‘lsa, ∫ f x dx( ) ≥ 0 bo‘ladi.
a b b
6. x∈[a b, ] da f x( ) < g x( ) bo‘lsa, u holda ∫ f x dx( ) ≤ ∫ g x dx( ) bo‘ladi.
a a
1. Aniq integral nima?
2. Egri chiziqli trapetsiya yuzini hisoblash masalasini ayting. Misollarda tushuntiring.
3. Nyuton–Leybnis formulasi nima? Uning mazmun-mohiyatini ayting.
4. Aniq integralning xossalarini ayting. Misollarda tushuntiring.
Aniq integrallarni hisoblang (36 – 41):
|
2 36. 1) ∫3x dx2 ; |
2 2) ∫2xdx; |
|
4 3) ∫ 5xdx; |
|
2 4) ∫8⋅x dx3 ; |
![]()
![]() 0 0 1
0 0 1
e 41
1
![]() 5) ∫1
5) ∫1 ![]() x
dx; 6)
3
x
dx; 6)
3
![]() x dx; 7) 1 x
dx; 8)
∫0 2xdx;
x dx; 7) 1 x
dx; 8)
∫0 2xdx;
![]()
![]() 4 27 3 dx 3
4 27 3 dx 3
2
9) ∫![]() dx; ; ;
12) ∫x x dx+1 .
dx; ; ;
12) ∫x x dx+1 .
![]()
![]()
![]()
![]() 10 πp
10 πp
cos(2x )dx; 2) ∫ sin 22 xdx;
−πp
3) sin3 cos3x xdx; 4) ∫(cos2 2x −sin 2 )2 x dx.
0
38. 1) ![]() e
dx2x ; 2)
e
dx2x ; 2) ![]() e dx4x ; 3)
e dx4x ; 3) ![]() ( ) .
( ) .
![]() (x 3
))(x x 1)dx; 2)
(x 3
))(x x 1)dx; 2) ![]() x x dx;
x x dx;
−1
3 −1
1 2 1 1
![]()
![]() 3) ∫1
(x
+
x)
dx; 4) −∫2 x2 (1−
x)dx.
3) ∫1
(x
+
x)
dx; 4) −∫2 x2 (1−
x)dx.
6 3 ![]()
dx dx 4 4
![]() 40*. 1)
40*. 1) ![]() ; 2)
∫0 x
+1; 3) ∫0 (sin
2x +cos 2 )x dx.
; 2)
∫0 x
+1; 3) ∫0 (sin
2x +cos 2 )x dx.
![]()
![]()
![]()
![]() x 1dx; 2) dx;3) .
x 1dx; 2) dx;3) .
42*. 1) Shunday a va b sonlarni topingki, f (x)=a·2x+b funksiya f ′(1) = 2,
3
∫ f x dx( ) = 7 shartlarni qanoatlantirsin.
0
b
![]() 2) b x dx b tengsizlik bajariladigan barcha b>1 sonlarni
2) b x dx b tengsizlik bajariladigan barcha b>1 sonlarni
toping.
43*. 1) ![]() tengsizlik
bajariladigan barcha b
tengsizlik
bajariladigan barcha b
sonlarni toping.
a
2) Qanday a>0 sonlar uchun ∫
e
dxx ![]() tengsizlik bajariladi?
tengsizlik bajariladi?
−a
44. f (x) funksiyani a ning ixtiyoriy qiymatida tengliklar bajariladigan qilib tanlang:
a a
1) ∫ f x dx( ) = 2a2 −3a; 2) ∫ f x dx( ) = 4a −a2;
0 0
a a
3)
![]() f x dx a3
f x dx a3 ![]() a2; 4)
a2; 4) ![]() .
.
0
Integrallarni hisoblang (45 – 46):
![]() (e 1)
dx; 2)
(e 1)
dx; 2) ![]() 10x
2 x dx; 3)
10x
2 x dx; 3) ![]() (e 1) dx;
(e 1) dx;
−2 0
ln3 ln5
4)
![]()
![]() 3 6x x dx; 5) ∫ e
dx−3x ; 6) ∫ e
dx2x .
ln2 ln3
3 6x x dx; 5) ∫ e
dx−3x ; 6) ∫ e
dx2x .
ln2 ln3
1 x x 1 x−1 x−1 e−1
2
![]() +3 2 +5 2xdx
+3 2 +5 2xdx
46*. 1)∫ x+1 dx; 2) ∫ ![]() x dx; 3) ∫ 2 ;
x dx; 3) ∫ 2 ;
![]() 0 6 0 10 0 x
+1
0 6 0 10 0 x
+1
e+2
2xdx
4)
![]() ∫
2
.; x − 2
∫
2
.; x − 2
![]() 1 x x
1 x x
3 4+
5)
![]() x dx
; 6) .
x dx
; 6) .
3
|
1) a=1, b=2, f (x)=x3; |
|
2) a=2, b=4, f (x)=x2; |
|
3) a=–2, b=1, f (x)=x2+2; |
|
4) a=1, b=2, f (x)=x3+2; |
47.![]()
![]() x=a, x=b to‘g‘ri chiziqlar, Ox
o‘qi va y=f (x) funksiya grafigi bilan chegaralangan egri
chiziqli trapetsiyaning yuzini toping. Mos rasm chizing:
x=a, x=b to‘g‘ri chiziqlar, Ox
o‘qi va y=f (x) funksiya grafigi bilan chegaralangan egri
chiziqli trapetsiyaning yuzini toping. Mos rasm chizing:
![]() 2π
2π
5) ![]() a
=,
b = , f
x( )
=
sin
x; 6) a =,
b =, f x( )
=
cos
x.
a
=,
b = , f
x( )
=
sin
x; 6) a =,
b =, f x( )
=
cos
x.
3
48.Ox o‘qi va berilgan parabola bilan chegaralangan shaklning yuzini toping:
1) y = 9 − x2; 2) y =16 − x2; 3) y = −x2 + 5x − 6;
4) y = −x2 + 7x −10; 5) y = −x2 + 4x; 6) y = −x2 − 3 .x
|
49. 1) y = −x2 + 2x, y = 0; |
|
2) y = −x2 + 3x +18, y = 0; |
|
3) y = 2x2 +1, y = 0, x = −1, x =1; |
|
4) y = −x2 + 2x, y x= . |
|
50. 1) y = −2x2 + 7x, y = 3,5 − x; |
|
2) y x= 2, y = 0, x = 3; |
|
3) y x= 2, y = 0, y = − +x 2; |
|
|
Quyidagi chiziqlar bilan chegaralangan shaklning yuzini toping. Mos rasm chizing (49 – 50):
1 2x
5) ![]() y = ⋅
x
,
y = a⋅ x
; 6) y =
2
, y = 2,x =
0
;
y = ⋅
x
,
y = a⋅ x
; 6) y =
2
, y = 2,x =
0
;
a
![]() 7) y = lg
x y, = 0, y =
2,x
=
0.
7) y = lg
x y, = 0, y =
2,x
=
0.
x3
1.
f x( ) = ![]() − cos3x funksiyaning barcha boshlang‘ich funksiyalarini
− cos3x funksiyaning barcha boshlang‘ich funksiyalarini
2
toping.
2.
![]()
![]() Agar F()
=1,
bo‘lsa, f x( ) = funksiyaning boshlang‘ich funk-
Agar F()
=1,
bo‘lsa, f x( ) = funksiyaning boshlang‘ich funk-
siyasi F(x) ni toping.
3.
Hisoblang: ![]() ( 6 9) .
( 6 9) .
π x
4.
Hisoblang: ![]() sin .
sin .
5. Ox o‘qi, x=–1 va x=2 to‘g‘ri chiziqlar va y=9–x2 parabola bilan chega ralangan egri chiziqli trapetsiyaning yuzini hisoblang.
x4
1.
f x( ) = ![]() + sin
4x funksiyaning barcha boshlang‘ich
funksiyalarini
+ sin
4x funksiyaning barcha boshlang‘ich
funksiyalarini
3
toping.
1 3
2.
Agar F ![]()
=
2
bo‘lsa, f x( ) =
=
2
bo‘lsa, f x( ) = ![]() 3 funksiyaning boshlang‘ich funk-
3 funksiyaning boshlang‘ich funk-
2 (2 − 5 )x siyasi F(x) ni toping.
3.
Hisoblang: ![]() .
.
–3
4.
Hisoblang: π∫
cos
![]() x dx
x dx
–π 2
5. Ox o‘qi, x=–2 va x=3 to‘g‘ri chiziqlar va y=x 2–1 parabola bilan chega ralangan egri chiziqli trapetsiyaning yuzini hisoblang.
JAVOBLAR
1. a) Puls chastotasi – bu yurakning bir minutda qancha urishini ko‘rsatuvchi belgi. Demak, bir minutda Madinaning yuragi 67 marta uradi. xato
b) ![]() 4020. 2. a) ≈ 0,001500 . Sifat ortdi; b) ≈ 0,15. 3. Ma’ruf unumliroq so‘z
4020. 2. a) ≈ 0,001500 . Sifat ortdi; b) ≈ 0,15. 3. Ma’ruf unumliroq so‘z
ishlagan. 4. a) ≈0,000177 mm . 5. 89 km yoki 89m . 6. a) 0,1 m ; b) 0,9 m ; km soat s s s
c) 0,5 m . 7. 1) a) 3,1 dona ; 4,22 dona ; b) doza 2 grammdan 8 grammgacha
s g g oshirilganda hasharotlar soni tez kamayadi, keyin esa kamayishi sust bo‘ladi. 8. a) 7; b) 7; c) 11; d) 16; e) 0; f) 5. 9. a) 5; b) 7; c) c. 10. a) –2; b) 7;
c) –1; d) 1. 11. a) –3; b) –5; c) –1 d) 6; e) –4; f) –8; g) 1; h) 2; i) 5.
1 1
![]()
![]() 13. a) 3x2; b) −x2
; c) 2 x ; d) 0. 15. a) 2; b) 6x + 5; c) 6x2+8x +6.
13. a) 3x2; b) −x2
; c) 2 x ; d) 0. 15. a) 2; b) 6x + 5; c) 6x2+8x +6.
16*. a) f ' (x)=a; b) f '(x)=2ax + b; c) f '(x)=3ax2 + 2bx + c. 20. 1) 4x3; 2) –2x–3;
–4. 21. 2) –x–2+1; 4) 4x3+3x2+2x–1+x–2+2x–3. 22. 2) 1; 4)− 1 . 3) –3x
![]() (2
x( x −1) )2
(2
x( x −1) )2
![]()
![]() 23. 2) 53,25. 24. 2) –3; 4) 2. 25. 2) −
4 + 1
; 4) 2x − 2
. 26. 2) 3(x+2)2; 4) 2x .
23. 2) 53,25. 24. 2) –3; 4) 2. 25. 2) −
4 + 1
; 4) 2x − 2
. 26. 2) 3(x+2)2; 4) 2x .
x2 4 x3
2x9 + 4x3
27. 3) − ![]() 6 2
; 4) (x −1)
6 2
; 4) (x −1)
![]() 1 3 – 4; 8) 7x6 +3x2–3x–4–7x–8. 28. 2) 0;
1 3 – 4; 8) 7x6 +3x2–3x–4–7x–8. 28. 2) 0;
− 2 ; 6) 4x
(x −1)
![]()
![]()
![]() 4) cos2 x
; 6) xln2 ; 8) 1+lnx; 10) 2ex
− x −
x2 . 29. 2) 2excosx; 4) x2 ;
4) cos2 x
; 6) xln2 ; 8) 1+lnx; 10) 2ex
− x −
x2 . 29. 2) 2excosx; 4) x2 ;
![]() 6) 5+ 1 + 1 ; 8) 3(2+x)2. 30. 2) 11. 31. 2) 0 . 32. 2) − 12 ; 4) − 2
1 2 ;
6) 5+ 1 + 1 ; 8) 3(2+x)2. 30. 2) 11. 31. 2) 0 . 32. 2) − 12 ; 4) − 2
1 2 ;
![]() 2
x 33 x2 cos
x sin xcos x
2
x 33 x2 cos
x sin xcos x
![]() 2 cosx ; 8) xcosx. 33. 2) 1. 34. 2) nπ, n∈z; 4) 1. 35. 1) 12 −1;
2 cosx ; 8) xcosx. 33. 2) 1. 34. 2) nπ, n∈z; 4) 1. 35. 1) 12 −1;
6) 2xsinx+x ∙
![]()
![]() 2) 4x2–1. 36. 2) ; 4) . 37. 2) x4 ; 4) x2–1. 38. 2) x3+3x2+3x+1; 4) x6 + 1. 2
2) 4x2–1. 36. 2) ; 4) . 37. 2) x4 ; 4) x2–1. 38. 2) x3+3x2+3x+1; 4) x6 + 1. 2
1− x x
39. x2–2x. 43. 2) esinxcosx; 4) sin2x; 6) ; 8) 20(2x–1)9. 44. 3) –tgx;
![]()
![]()
![]() 8) –30x2cos29x∙sinx+2xcos30x; 9) 5ctgx −
5ln2x
.
45. 2) y=3x–4; y=3x–4;
y=3x–4. x s ni x
8) –30x2cos29x∙sinx+2xcos30x; 9) 5ctgx −
5ln2x
.
45. 2) y=3x–4; y=3x–4;
y=3x–4. x s ni x
4) y=–x–2; y=8x+16; y=–4x. 46. 2) y=7x–6. 47. 4) 0 va ; 6) 0 va . 48. 1) y=x–2;
y=–17x–11; y=–5x+1. 49. 2) 0,1 ; 0,331 . 50. 2) a) 0,2718; b) 9,06; 4) a) 0,938127;
1 1 1 1 1−ln x
b) 31,2709. 51. 2) a) 0; b) 0; 4) a) 0,119401; b) 11,9401 . 52. 1) 4; 2) –7; 3) 6; 4) 19/28; 5) 0. 53. 2) 29; 4) 32x–3; 6)18–2x; 8) 48x2+10x–2. 54. 1) a) 15; b) 15; c)
15; d) 15; 4) a) –29; b) 12; c) 5; d) –1. 55. 2) 3(x+2)2 ; 4) 1–x–2. 56. 1) 12; 2) 3.
![]() 1 x 1
1 x 1
![]()
![]() 57. 15 m/s. 58. 3) 5 4 +
tgx+ cos2 x
− xln3
; 10) 7xx7ln7+7x·7x6 ; 12) 2 – cosx;
57. 15 m/s. 58. 3) 5 4 +
tgx+ cos2 x
− xln3
; 10) 7xx7ln7+7x·7x6 ; 12) 2 – cosx;
5 x
14) 8–2x. 59. 2) 4; 4) 2. 60. 2) Ø. 61. 1 va 2 . 62. 2) –2x–3–1 . 63. 2) 2,75.
64. 2) ![]() x2 +16x
−24
; 4) 6x2+8x+5 ; 6) 14x+12. 65. 2)
x2 +16x
−24
; 4) 6x2+8x+5 ; 6) 14x+12. 65. 2) ![]() −2x7 −4x5 −5x4 +
21x2 +7
. 2 5 2
−2x7 −4x5 −5x4 +
21x2 +7
. 2 5 2
(x +8) (x +7)
![]()
![]() 5x(4cosx–6sinx);
4) 1−2ln
x .
67. 2) –4; 4) − 12 −
1
.
5x(4cosx–6sinx);
4) 1−2ln
x .
67. 2) –4; 4) − 12 −
1
.
66. 2) e 3
x sin 1 20
34
![]()
![]() 2cosx; 2) – tgx
; 4) 35tg2 x
; 8) (2x–10)lncosx–(x2–10x+7)tgx. 68. 1) 2xsinx+x
2cosx; 2) – tgx
; 4) 35tg2 x
; 8) (2x–10)lncosx–(x2–10x+7)tgx. 68. 1) 2xsinx+x
14) o‘sish: ![]() ; kamayish: Ø.
; kamayish: Ø.
70. 2) –3; 3 . 4) 0. 6) Ø. 8) 0; –1.
71. 2) lokal minimum x=4; lokal maksimum mavjud emas. 4) lokal minimum x=5; lokal maksimum x=–5.
6) lokal minimum x=0,75; lokal maksimum mavjud emas.
8) lokal minimum x= 2nπ, n∈ℤ; lokal maksimum x= π+2nπ, n∈ℤ.
72. 2) o‘sadi (–1; 1); kamayadi: (–∞;
–1) U (1; +∞).![]()
4) o‘sadi: ![]() ; kamayadi:
; kamayadi: ![]() ;
;
6) o‘sadi: Ø ;
kamayadi: ![]() .
.
73. 2) eng katta qiymat: 57; eng kichik qiymat: –55.
4) eng katta qiymat:
84; eng kichik qiymat: −![]()
76. 5625m2. 80. 80 m. 83. 1) 5 s; 2) 250 m/s; 3) ![]() m.
m.
m3
87. 1) 4m3; 2)
5324 m3; 3)
407 ![]() ; min
; min
89. 1) 30 ta; 2) 1800000 so‘m .
91. d) 24,52, –0,1; e) 40,52, 9,86. 93. g) 2,0004. 94. e) 0,9302.
95. d) 0,526. 96. d) 0,1247. 112. 1) eng katta 13; eng kichik 13; 3) eng
katta mavjud emas; eng kichik 5; 5) eng katta mavjud emas; eng kichik ![]() .
.
113. 2) y=13x+4;y=13x+4; y=13x+4. 114. 1) mavjud emas. 115. 3) mavjud emas.
![]() 5
2
5
2
117.
![]()
![]()
![]()
![]()
![]() 1) –1; 2) 0; 3) –; 4) –; 5) 75; 6) ; 7) –; 8) ; 9) – 2
.
1) –1; 2) 0; 3) –; 4) –; 5) 75; 6) ; 7) –; 8) ; 9) – 2
.
2
118. 1) 19; 10; 2) 27;30; 3) 77; 30; 4) 0; –8.
3
![]() 13 5
2
13 5
2
119.
![]() 1) 1; 2) 0; 3) –
1) 1; 2) 0; 3) – ![]() ;
4) –
;
4) – ![]() ; 5) 75; 6) ; 7) – ;
8) ; 9) 2 ; 10) 0.
; 5) 75; 6) ; 7) – ;
8) ; 9) 2 ; 10) 0.
4 2 2 16 2
120. 1) 10; 6. 2) 15; 18. 3) 225; 80.
x 1 3 20
121.
![]()
![]() 1) –2x+1; 2) cosx+sinx; 4) 4 ln4–cosx;
6)
1) –2x+1; 2) cosx+sinx; 4) 4 ln4–cosx;
6) ![]() – 20x+1. 122. 1) 4x ; 3) 1+ ;
x
6) ex(sinx+cosx);8) 20sinx+2(10x–1)cosx.
– 20x+1. 122. 1) 4x ; 3) 1+ ;
x
6) ex(sinx+cosx);8) 20sinx+2(10x–1)cosx.
![]() π 2
π 2
123. 1) ; 0; 2) 3; 3; 3) –2π +1; π+1. 4) – π; + ; 5) 1; 0; 6) 0; ;
2 2
![]() 7) 1– ; – . 8) 3; –3 2
.
7) 1– ; – . 8) 3; –3 2
.
124. 1) 12; 2)72. 126. 1) 0; 2) 600 000. 127. 2) –sin2x.
|
128. 2) o‘sish: (–∞; +∞); |
kamayish: Ø. |
|
4) o‘sish: Ø; |
kamayish: (–∞; 0) U (0; +∞). |
|
6) o‘sish: (–∞; +∞); |
kamayish: Ø. |
|
8) o‘sish: (0; +∞); |
kamayish: (–∞; 0). |
129. 2) ![]() . 4) 0; 6)
3; –3; 8) 0; −
. 4) 0; 6)
3; –3; 8) 0; −![]() .
.
130. 2) lokal minimum: x=9. lokal maxsimum: mavjud emas.
131. 2) eng katta: 81; eng kichik: –6. 134. 62 500 m2.
![]() 143.
1) 3e3x; 2) esinxcosx; 3) 3cos(3x+2); 4) 8(2x+1)3; 144. 1) e8x+4; 2) e8x2+4x; 3) 4e2x+2; 4) 16x
+10
.
143.
1) 3e3x; 2) esinxcosx; 3) 3cos(3x+2); 4) 8(2x+1)3; 144. 1) e8x+4; 2) e8x2+4x; 3) 4e2x+2; 4) 16x
+10
.
145. 1) 10x(x2+1)4; 3) ; 8) –esin(cosx)·cos(cosx)·sinx.
|
146. 1) o‘sadi: (–∞; 0,5); |
|
kamayadi: (0,5; –∞); |
|
3) o‘sadi: (–1; 1); |
|
kamayadi: (– ∞; –1)U(1;+ ∞). |
|
4) o‘sadi: (–∞; +∞); |
|
kamayadi: Ø. |
|
7) o‘sadi: (–∞; +∞); |
|
kamayadi: Ø. |
|
8) o‘sadi: (1; +∞); |
|
kamayadi: (– ∞; 1). |
147. 1) statsionar nuqtalari: 1 va 3; lokal maksimum: 0; lokal minimum: –4.
![]() 2. 2) x6 + C; 4) x
2. 2) x6 + C; 4) x![]() +C
; 6) sinx + C; 8) sin2xx+ C. 3. 2)
+C
; 6) sinx + C; 8) sin2xx+ C. 3. 2) ![]() πpx +C
;
πpx +C
;
lnπp
![]()
![]()
![]()
![]()
![]() 4) ax +C
; 6) eπx +C . 4. 4) 1 ln x C+sin5x
C+
; 6)= cos2x+C.
4) ax +C
; 6) eπx +C . 4. 4) 1 ln x C+sin5x
C+
; 6)= cos2x+C.
. 5. 4)
ln a π a
6. 4) ![]() x–1)4+C. 7. 2) –
x–1)4+C. 7. 2) –
![]() xx3+x2+5x+2; 4) sinx+4. 8. 1) 2x2 + 8x + 11;
xx3+x2+5x+2; 4) sinx+4. 8. 1) 2x2 + 8x + 11;
2) − + +x2 3x 2,5; 3) 9 2 9x 15 8, ; 4) x2 − 6x + 10. 10. 1) 8 − 2x + 4; x + +
2 4 x
2) ![]() ; 3) x 3 − x + 6; 4) x 5 + 7x + 1. 11. 1)
; 3) x 3 − x + 6; 4) x 5 + 7x + 1. 11. 1) ![]() 4 ( ) 4; x
4 ( ) 4; x
1 k+1
![]()
![]() 2) ⋅( x )
2) ⋅( x ) ![]() ;
3)
;
3) ![]() ⋅(kx +b) k + k .
⋅(kx +b) k + k .
5 5 8 8 k +1 k +1
![]() 12. 1) 5 lnǀx
−2ǀ + 7; 2) 3 lnǀx +1ǀ +1; 3) sin x + 7;
4) −cos x + 9. 14. 2) 15⋅sin5x + 53; 4) −3cos
12. 1) 5 lnǀx
−2ǀ + 7; 2) 3 lnǀx +1ǀ +1; 3) sin x + 7;
4) −cos x + 9. 14. 2) 15⋅sin5x + 53; 4) −3cos ![]() 3x +6. 15. 1) x 3 − 4; 2) x 4 − 15. 16. 2) x 8 + x 5; 4) − 53⋅ x13 − 43 ⋅ x14 .
3x +6. 15. 1) x 3 − 4; 2) x 4 − 15. 16. 2) x 8 + x 5; 4) − 53⋅ x13 − 43 ⋅ x14 .
![]() 17. 2) −7 cos x + 4 sin x; 4)
5 e x +2 sin x. ;
17. 2) −7 cos x + 4 sin x; 4)
5 e x +2 sin x. ;
![]()
![]()
![]()
![]() 6) −2cos (x − 3) − 4 ln ǀx −
2ǀ. x ) C; 4) )
C; 6)
6) −2cos (x − 3) − 4 ln ǀx −
2ǀ. x ) C; 4) )
C; 6)
(3x 2) x C; 4) x n ;
![]() 4)
4) ![]() 22. 2) 1 x5 + 1sin3x+4x C+ ; 4 −
3·cos
22. 2) 1 x5 + 1sin3x+4x C+ ; 4 −
3·cos
![]() x +C
.
x +C
.
5 33
23. 2) −1cos4x C+ . 24. 1) −1cos8x− 1 cos4x;. 25. 2) ln +C; 4) ln ǀx − 4ǀ + C.
4 16 4
26. 2) x − arctg x + C; 4) ![]() x+C. 27. 2) − 4 1( +x2 2) +C; 4) –
x+C. 27. 2) − 4 1( +x2 2) +C; 4) – ![]() ctg2x+C.
ctg2x+C.
![]()
![]()
![]()
![]() 28. 2) .; 4) xx+C. 29. 2) – cos5 +3 4)
28. 2) .; 4) xx+C. 29. 2) – cos5 +3 4)
x x+ − − +2 1 2x C. 33. 1) sin x x− cosx C+ ; 2) x2 ⋅sin x −2sin x + 2xcos x C+ ;
3) 1 ⋅x2 ln x − 1 x C2 + ; 4) x⋅arctgx − 1 ln(1+ x2)+C.
2 4 2
34. 1) 1 ⋅(xsin2x + 1 cos2x C)+ ; 3) 9sin x −3x⋅cos x +C.
2 2 3 3
![]() = ,
= ,
7(ln2 2–1)
b= ![]() 2 ; 2) b = 2. 43. 1) b = 3; 2) a > ln 2. 44. 1) f(x) = 4x
− 3; 2) f(x) = 4 − 2x; 3)
2 ; 2) b = 2. 43. 1) b = 3; 2) a > ln 2. 44. 1) f(x) = 4x
− 3; 2) f(x) = 4 − 2x; 3)
3ln 2
f(x) = x2 − 3x; 4) f(x) = 1 + 2x + cos x. 45. 2) ![]() ; 6) 8. 46. 2)
; 6) 8. 46. 2) ![]() ; 4) 1. 47. 2)
; 4) 1. 47. 2)
![]()
![]()
![]()
![]() 1 4
1 4
; 4) 1−. 48. 2) 85
![]() . 49. 1)
. 49. 1) ![]() ; 2) 121,5; 3) ; 4) .
; 2) 121,5; 3) ; 4) .
2 3 3
50. 1) 9; 2) 9; 3) 4,5;
Foydalanilgan va tavsiya etiladigan adabiyotlar
1. Ш.A. Алимов и др. Алгебра и начала математического анализа, учебник для 10–11 класса. Учебник для базового и профильного образования, Москва, “Просвещение”, 2016.
2. Mal Coad and others. Mathematics for the international students. Mathematical Studies SL 2nd edition. Haese and Harris publications. 2010.
3. А.Н. Колмогоров и др. Алгебра и начала анализа. Учебное пособие для 10–11 классов. Москва, “Просвещение”, 2018.
4. Э. Сайдаматов и др. Алгебра и основы математического анализа. часть 2 учебное пособие, Ташкент, “Ilm ziyo”, 2016.
5. A.U. Abduhamidov va boshqalar. Algebra va matematik analiz asoslari, 1- qism, Toshkent, “O‘qituvchi”, 2012.
6. Н.П. Филичева. Уравнения и системы уравнений: Учебнометодическое пособие. “Рязань”. 2009.
7. М.И. Исроилов. Ҳисоблаш методлари. Тошкент, “Ўқитувчи”, 1988.
8. Г.К. Муравин и др. Алгебра и начала анализа. Учебник для 10 класса. Москва, “Дрофа”, 2006.
9. Алгебра. Учебное пособие для 9–10 классов. Под ред. Н.Я. Виленкина. Москва, “Просвещение”, 2004.
10. Г.П. Бевз и др., Алгебра и начала анализа. Учебник для 11 класса. Киев, 2011.
11. http://www.ams.org/mathweb/ – Internetda matematika (ingliz tilida).
12. “Математика в школе” jurnali.
13. Fizika, matematika va informatika. Ilmiy-uslubiy jurnal (2001- yildan boshlab chiqa boshlagan).
14. M.A. Mirzaahmedov, Sh.N. Ismailov. Matematikadan qiziqarli va olimpiada masalalari. I qism, Toshkent, “Turon-Iqbol”, 2016.
15. Matematikadan qo‘llanma, I va II qismlar. O‘qituvchilar uchun qo‘llanma.Prof. T.A. Azlarov tahriri ostida. Toshkent, “O‘qituvchi”, 1979.
16. M.A. Mirzaahmedov, D.A. Sotiboldiyev. O‘quvchilarni matematik olimpia dalarga tayyorlash. Toshkent, “O‘qituvchi”, 1993.
17. M.A. Mirzaahmedov, Sh.N. Ismoilov. 10-sinf uchun “Algebra va analiz asosolari”dan testlar, G‘.G‘ulom NMIU, Toshkent, 2005.
18. В.М. Говоров и др., Сборник конкурсных задач по математике, Наука, М., 1984.
19. T.A. Azlarov, X. Mansurov. Matematik analiz asoslari. 3-nashr, “Universitet”, Toshkent, 2005.
20. Б.П. Демидович. Сборник задач и упражнений по математическому анализу, Наука, М., 1990.
21. Силм А.Ш., Математикадан тест саволлари, Тошкент, 1996.
22. Материалы ЕГЭ по математике, М., 2016.
23. Е.П. Кузнецова, Г.А. Муравьева, Сборник задач по алгебре, 11-класс, “Мнемозика”, 2016.
24. А.Г. Мордкович, Сборник задач по алгебре, 10-11 классы, “Мнемозика”, 2016.
25. М.И. Шкиль, З.И. Слепкаль, Алгебра, учебник для 11 класса, Киев, 2016.
26. Е.П. Нелина, О.Е. Долгова, Алгебра, учебник для 11 класса, Киев, 2015.
27. http://www.uzedu.uz – Xalq ta’limi vazirligining axborot ta’lim portali.
28. http://www.eduportal.uz – Multimedia markazi axborot ta’lim portali.
29. http://www.problems.ru – Matematikadan masalalar izlash tizimi (rus tilida).
30. http://matholymp.zn.uz – O‘zbekistonda va dunyoda matematik olimpiadalar.
MUNDARIJA
I bob. HOSILA VA UNING TATBIQLARI .......................................3
1–2. O‘zgaruvchi miqdorlar orttirmalarining nisbati va uning ma’nosi.
Urinma ta’rifi. Funksiya orttirmasi ................................................3
3–4. Limit haqida tushuncha ................................................................12
5–6. Hosila, uning geometrik va fizik ma’nosi .....................................16
7–9. Hosilani hisoblash qoidalari ......................................................... 24
10–12. Murakkab funksiyaning hosilasi .................................................. 30
13–14. Funksiya grafigiga o‘tkazilgan urinma va
normal tenglamalari ...................................................................... 34
15–17. Masalalar yechish ..........................................................................39
18–21. Hosila yordamida funksiyani tekshirish
va grafiklarni yasash ................................................................... 42
22–25. Geometrik, fizik, iqtisodiy mazmunli ekstremal masalalarni
yechishda differensial hisob usullari ............................................. 50 26–28. Taqribiy hisoblashlar ..................................................................... 56
29–32. Hosila yordamida modellashtirish .................................................62
33–36. Masalalar yechish ..........................................................................73
II bob. INTEGRAL VA UNING TATBIQLARI ............................. 79
37–39. Boshlang‘ich funksiya va aniqmas
integral tushunchalari ....................................................................79
40–43. Integrallar jadvali. Integrallashning eng sodda qoidalari ............ 86
44–46. Aniq integral. Nyuton–Leybnis formulasi .................................... 96
Javoblar .......................................................................................106
GEOMETRIYA
![]() I BOB. FAZODA KOORDINATALAR SISTEMASI VA VEKTORLAR
I BOB. FAZODA KOORDINATALAR SISTEMASI VA VEKTORLAR
1. FAZODA KOORDINATALAR SISTEMASI
Tekislikda dekart koordinatalari sistemasi bilan quyi sinflarda ta nishgansiz. Fazoda koordinatalar sistemasi ham tekislikdagiga o‘xshash kiritiladi. O nuqtada kesishuvchi va koordinata boshi shu nuqtada bo‘lgan o‘zaro perpendikular uchta Ox, Oy va Oz koordinata o‘qlarini qaraymiz.
Bu to‘g‘ri chiziqlarning har bir jufti orqali Oxy, Oxz va Oyz tekisliklar o‘tkazamiz (1- rasm). Fazoda to‘g‘ri burchakli dekart koordinatalari sistemasi shu tariqa kiritiladi va unda
O nuqta – koordinatalar boshi,
Ox, Oy va Oz to‘g‘ri chiziqlar – koordinata o‘qlari,
Ox – abssissalar, Oy – ordinatalar va Oz o‘qi – applikatalar o‘qi, Oxy, Oyz va Oxz tekisliklar – koordinatalar tekisliklari deb ataladi.
Koordinatalar tekisliklari fazoni 8 ta oktantaga (nimchorakka) bo‘ladi (1- rasm).
Fazoda ixtiyoriy A nuqta berilgan bo‘lsin. Bu nuqtadan Oxy, Oyz va Oxz koordinata tekisliklariga perpendikular tekisliklar o‘tkazamiz (2- rasm). Bu tekisliklardan biri Ox o‘qini Ax nuqtada kesib o‘tadi.
Ax nuqtaning x o‘qidagi koordinatasi A nuqtaning x – koordinatasi yoki abssissasi deb ataladi.
A nuqtaning y – koordinatasi (ordinatasi) hamda z – koordinatasi (applikatasi) ham shu tariqa aniqlanadi.
A nuqtaning koordinatalari A(x; y; z) yoki qisqaroq (x; y; z) tarzda belgilanadi. 3- rasmda tasvirlangan nuqtalar quyidagi koordinatalarga ega: A(0; 5; 0), B(4; 0; 0), M (0; 5; 4), K (2; 3; 4), P (–2; 3; –4).
1- masala. Fazoda dekart koordinatalari sistemasi kiritilgan. Undagi A(2; 3; 4) nuqtaning o‘rnini aniqlang.
Yechish. Koordinata boshidan Ox va Oy o‘qlarining musbat yo‘nalishida, mos ravishda, OAx = 2 va OAy = 3 kesmalarni qo‘yamiz (4- rasm).
Ax nuqtadan Oxy
tekislikda yotgan va Oy o‘qiga parallel to‘g‘ri chiziq o‘tkazamiz. Ay nuqtadan Oxy
tekislikda yotgan va Ox o‘qiga parallel to‘g‘ri chiziq o‘tkazamiz. Bu
to‘g‘ri chiziqlar kesishish nuqtasini A1 bilan belgilaymiz. A1 nuqtadan Oxy
tekislikka perpendikular o‘tkazamiz va unda Oz o‘qining musbat
yo‘nalishida AA1 = 4 kesma qo‘yamiz. Hosil bo‘lgan A(2; 3; 4) nuqta
izlanayotgan nuqta bo‘ladi. ![]()
Zamonaviy raqamli-dasturli boshqariladigan stanoklar va avtomatlashtirilgan robotlar uchun koordinatalar sistemasidan foydalanib dasturlar tuzi ladi va ular asosida metallarga ishlov beriladi (5- rasm).
Ikkita A(x1; y1; z1) va B(x2; y2; z2) nuqtalar berilgan bo‘lsin.
1. Avval AB to‘g‘ri chiziq Oz o‘qiga parallel bo‘lmagan holni qaraymiz (6- rasm). A va B nuqtalar orqali Oz o‘qiga parallel chiziqlar o‘tkazamiz. Ular Oxy tekislikni Az va Bz nuqtalarda kesib o‘tsin.
Bu nuqtalarning z koordinatasi 0 ga teng bo‘lib, x va y koordinatalari esa mos ravishda A, B nuqtalarning x va y koordinatalariga teng.
Endi B nuqta orqali Oxy tekislikka parallel a tekislik o‘tkazamiz. U AAz to‘g‘ri chiziqni biror C nuqtada kesib o‘tadi.
Pifagor teoremasiga ko‘ra: AB 2 = AC2 + CB2.
![]() Lekin CB
= AzBz, AzBz2 = (x2 – x1)2 + (y2 – y1)2 va AC = |z2 – z1|. Shuning uchun AB (x2 x1)2 (y2 y1)2 (z2 z21) .2.
Lekin CB
= AzBz, AzBz2 = (x2 – x1)2 + (y2 – y1)2 va AC = |z2 – z1|. Shuning uchun AB (x2 x1)2 (y2 y1)2 (z2 z21) .2.
2. AB kesma Oz o‘qiga parallel, ya’ni AB= |z2 – z1| bo‘lganda ham yuqoridagi formula o‘rinli bo‘ladi, chunki bu holda x1= x2, y1 = y2.
|
Demak, A va B nuqtalar orasidagi masofa:
|
|
|
|
(1) |
![]()
![]()
![]() Izoh.
(1) formula to‘g‘ri burchakli parallelepipedning o‘lchamlari a x2 x1
Izoh.
(1) formula to‘g‘ri burchakli parallelepipedning o‘lchamlari a x2 x1![]() , b y2 y1
, b y2 y1![]() , c z2 z1
, c z2 z1![]() bo‘l ganda, uning diagonali uzunligini ifodalaydi.
bo‘l ganda, uning diagonali uzunligini ifodalaydi.
Sfera va shar tenglamasi. Ma’lumki, A(a; b; c) nuqtadan R masofada yotgan barcha M(x; y; z) nuqtalar sferani tashkil qiladi (7- rasm). Unda (1) formulaga ko‘ra, markazi A(a; b; c) nuqtada radiusi R ga teng bo‘lgan sferada yotgan barcha nuqtalar koordinatalari (x – a)2 + (y – b)2 + (z – c)2 = R2 tenglikni qanoatlantiradi.
Unda, ravshanki, markazi A(a; b; c) nuqtada, radiusi R ga teng bo‘lgan shar tenglamasi (x – a)2 + (y – b)2 + (z – c)2 ≤ R2 tarzda ifodalanadi.
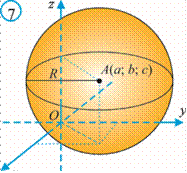
2- masala. Uchlari A(9; 3; –5), B(2; 10; –5), C(2; 3; 2) nuqtalarda bo‘lgan ABC uchburchakning perimetrini toping.
![]() Yechish:
ABC uchburchakning perimetri P
=AB+AC+BC. Ikki nuqta orasidagi masofa formulasi d
=
(x2
−x1)2
+
(y2
−y1)2
+
(z2
−z1)2 dan foydalanib uchburchak tomonlarini topamiz:
Yechish:
ABC uchburchakning perimetri P
=AB+AC+BC. Ikki nuqta orasidagi masofa formulasi d
=
(x2
−x1)2
+
(y2
−y1)2
+
(z2
−z1)2 dan foydalanib uchburchak tomonlarini topamiz:
AB (29)2 (10 3)2 ( 5 5)2 49 49 7 2,
AC (29)2 (3 3)2 (2 5)2 49 49 7 2,
BC (22)2 (3 10)2 (2 5)2 49 49 7 2.
Demak, ABC uchburchak teng tomonli va uning perimetri:
P 3 7 221 2 . Javob: 21 2 .
A(x1; y1; z1) va B(x2; y2; z2;) – ixtiyoriy nuqtalar bo‘lib, AB kesmaning o‘rtasi C(x; y; z) bo‘lsin (8- rasm).
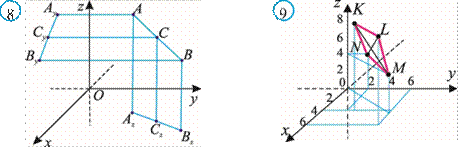
A, B va C nuqtalar orqali Oz o‘qiga parallel to‘g‘ri chiziqlar o‘tkazamiz. Ular Oxy tekislikni Az(x1; y1; 0), Bz(x2; y2; 0) va Cz(x; y; 0) nuqtalarda kesib o‘tsin.
Fales teoremasiga ko‘ra Cz nuqta Az Bz kesmaning o‘rtasi bo‘ladi. Unda tekislikda kesma o‘rtasining koordinatalarini topish formulasiga ko‘ra
x1x2 y1 y2 x , y .
2 2
z ni topish uchun Oxy tekislik o‘rniga Oxz yoki Oyz tekislikni olish kifoya. Bunda z uchun ham yuqoridagilarga o‘xshash formula hosil qilinadi.
|
x 1x2 , y y1 y2 x 2 2 |
z z 1z2 . 2 |
Shunga o‘xshash, berilgan AB kesmani λ nisbatda (AP : PB = λ) bo‘luvchi
P(x1; y1; z1) nuqtaning koordinatalari A va B nuqtalarning koordinatalari orqali
|
x +λx y +λy z +λz x =
1 2
, y = 1+λ 1+λ 1+λ |
formulalar yordamida topiladi. Ularning to‘g‘riligini mustaqil ko‘rsating.
3-masala. Uchlari M(3; 6; 4), N(0; 2; 4), K(3; 2; 8), L(6; 6; 8) nuqtalarda bo‘lgan MNKL to‘rtburchakning parallelogramm ekanligini isbotlang (9- rasm).
Isbot: Masalani yechishda diagonallari kesishish nuqtasida teng ikkiga bo‘linadigan to‘rtburchakning parallelogramm ekanligidan foydalanamiz. MK kesma o‘rtasining koordinatalari:
![]()
![]()
![]() x3; y4; z 6.
x3; y4; z 6.
NL kesma o‘rtasining koordinatalari:
![]()
![]()
![]() x3; y4; z x6.
x3; y4; z x6.
MKva NL kesmalar o‘rtalarining koordinatalari bir xil ekanini ko‘ramiz. Bu mazkur kesmalar kesishishini va kesishish nuqtasida ular teng ikkiga bo‘linishini bildiradi.
Demak, MNLK
to‘rtburchak – parallelogramm. ![]()
1. 10- rasmda tasvirlangan nuqtalarning koordinatalarini aniqlang.
2. Fazoda dekart koordinatalari sistemasi kiritilgan bo‘lib, undaA(0; 3; 1), B(–2; 0; 0), C(0; 0; 8), D(0; –9; 0), E(5; –1; 2), F(–6; 2; 1) nuqtalar berilgan. Bu nuqtalar qaysi a) koordinatalar o‘qda; b) koordinatalar tekisligida; c) oktantda yotadi?
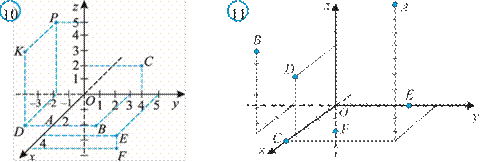
3. 11- rasmdagi nuqtalar koordinatalarini toping.
4. 12- rasmda belgilangan nuqtalarning koordinatalarini toping.
5.
![]() 13- rasmda diagonali 2 ga teng bo‘lgan kvadrat
tasvirlangan. Uning uchlari koordinatalarini toping.
13- rasmda diagonali 2 ga teng bo‘lgan kvadrat
tasvirlangan. Uning uchlari koordinatalarini toping.
6. A (3; 2; 4) nuqtaning koordinata tekisliklaridagi proyeksiyasi koordinatalarini toping.
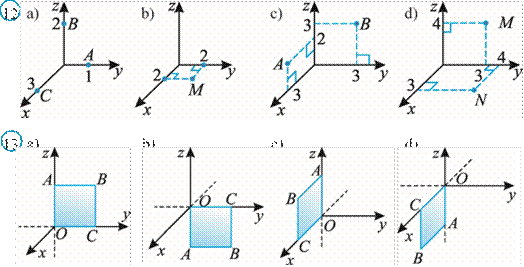
7. Fazoda dekart koordinatalari sistemasi kiritilgan bo‘lib, unda A (–1; 2; –3), B(0; 1; 2), C(0; 0; 5), D(–2; 2; 0), E(5; –1; 0), F(0; 2; 0), G(9; 0; 0), H(9; 0; 2), I(6; 3; 1), J(–6; 3; 5), K(–6; –2; 3), L(6; –2; 4), M(6; 3; –9), N(–6; 3; –8), O(–6; –3; –6), P(6; –3; –2) nuqtalar berilgan bo‘lsin. Bu nuqtalar qaysi koordinatalar o‘qida, kordinatalar tekisligida va oktantda yotadi? Quyida berilgan jadvalni berilgan namunalarga ko‘ra to‘ldiring.
|
Nuqta o‘rni |
Nuqta koordinatalari xususiyati |
Nuqta |
|
Ox o‘qi |
y=0, z=0 faqat x koordinata noldan farqli |
G(9; 0; 0) |
|
Oy o‘qi |
|
|
|
Oz o‘qi |
|
|
|
Oxz tekislik |
z=0, x va y koordinatalar noldan farqli |
D(–2; 2; 0) |
|
Oyz tekislik |
|
|
|
Oxz tekislik |
|
|
|
1- oktant |
x>0, y>0, z>0 |
I(6; 3; 1) |
|
2- oktant |
|
|
|
3- oktant |
|
|
|
4- oktant |
|
|
|
5- oktant |
|
|
|
6- oktant |
|
|
|
7- oktant |
|
|
|
8- oktant |
|
|
8. A(2; 0; –3) va B(3; 4; 0) nuqtalar orasidagi masofani toping.
9. A(3; 3; 3) nuqtadan a) koordinata tekisliklarigacha; b) koordinata o‘qlarigacha; c) koordinata boshigacha bo‘lgan masofalarni toping.
10. M (2; –3; 1) nuqtadan koordinata tekisliklarigacha bo‘lgan masofalarni toping.
11. Koordinata tekisliklarining har biridan 3 birlik masofada uzoqlashgan nuqtaning o‘rnini aniqlang.
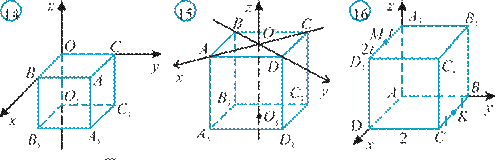
12. Agar OA=2√2 bo‘lsa, 14- rasmda tasvirlangan kubning uchlari koordinatalarini toping.
13. C(2; 5; –1) va D(2; 1; –6) nuqtalarning qaysi biri koordinata boshiga yaqin joylashgan?
14. Uchlari A(1; 2; 3), B(2; 3; 1), C(3; 1; 2) nuqtalarda bo‘lgan uchburchakning perimetrini toping.
15. Uchlari A(1; 2; 3), B(2; 3; 4), C(3; 4; 5) nuqtalarda bo‘lgan uchburchak mavjudmi?
16. A(–2; 0; 5), B(–1; 2; 3), C(1; 1; –3), D(0; –1; –1) nuqtalar parallelogramm uchlari ekanligini isbotlang.
17. ABC uchburchak turini aniqlang, uning perimetri va yuzini toping:
a) A (3; 0; 0), B (0; 3; 0), C (0; 0; 3); b) A (2; 0; 5), B (3; 4; 0), C (2; 4; 0); c) A (2; 4; –1), B (–1; 1; 2), C (5; 1; 2).
18. Oxy tekisligida yotuvchi va A(0; 1; –1), B(–1; 0; –1), C(0; –1; 0) nuqtalardan baravar uzoqlikda yotuvchi nuqtaning koordinatalarini toping.
19. A (1; 1;1),B (–1; 1; 1),C (–1; –1; 1),C1 (–1; –1; –1)nuqtalarABCDA1B1C1D1 kubning uchlari bo‘lsa, uning qolgan uchlari koordinatalarini toping.
20. Uchlari S (0; 0; 0), A (2; 0; 0), B (0; 2; 0), C (0; 0; 2) nuqtalarda bo‘lgan SABC piramidaning muntazam ekanligini isbotlang.
21. Markazi koordinatalar boshida, radiusi 5 ga teng bo‘lgan sfera va shar tenglamalarini yozing.
22. Markazi A (1; 2; 4) nuqtada, radiusi 3 ga teng bo‘lgan shar tenglamasini yozing.
23. Diametri uchlari A (–2; 1; 3), B (0; 2; 1) nuqtalarda yotgan sfera tenglamasini yozing.
24. Qalin qog‘ozdan kub modelini yasang. Uning bitta uchini koordinata boshi, undan chiquvchi qirralarni birlik ortlar sifatida olib, uning boshqa uchlari koordinatalarini toping.
25. AB kesma o‘rtasining koordinatalarini toping:
1) A(–1; 0; 0), B(1; 2; 0); 2) A(0; 0; 0), B(2; 2; 2); 3) A(–2; 4; 2), B(2; –4; 2),
![]()
![]()
![]()
![]() 4) A(1,2; –3; 6,3), B(–2,6; 3,2; –5,1); 5) A( 3; 2; 1– 2
), B(3 3; 1;1+ 2
).
4) A(1,2; –3; 6,3), B(–2,6; 3,2; –5,1); 5) A( 3; 2; 1– 2
), B(3 3; 1;1+ 2
).
26. 15- rasmda tasvirlangan kub qirralari o‘rtalarining va yoqlari mar-kaz larining koordinatalarini toping.
27. A(3;–1;4), B(–1;1;–8), C(2;1;–6), D(0;1;2) nuqtalar berilgan. a) AB va CD; b) AC va BD kesmalar o‘rtasining koordinatalarini toping.
28. M(1;–1;2) va N(–3;2;4) nuqtalar AB kesmani uchta teng bo‘lak larga ajratadi. AB kesma uchlarining koordinatalarini toping.
29. ABCD to‘rtburchakning tomonlari va A1B1C1D1 to‘g‘ri to‘rtburc hakning tomonlariga mos ravishda parallel. ABCD – to‘g‘ri to‘rtburchak ekanini isbotlang?
30. ABCD to‘g‘ri to‘rtburchakning A uchidan uning tekisligiga perpendikular AK to‘g‘ri chiziq o‘tkazilgan. K nuqtadan to‘g‘ri to‘rtburchakning boshqa uchlarigacha bo‘lgan masofalar 6 cm, 7 cm va 9 cm. AK kesmaning uzunligini toping.
31*.Fazoda A(3; 0; –1), B(–4; 1; 0), C(5; –2; –1) nuqtalar berilgan. Oyz tekislikda A, B, C nuqtalardan baravar uzoqlikda joylashgan nuqtani toping.
32. ABCD parallelogrammning uchlari: a) A(–2; –4; 3), B(3; 1; 7), C(4;2;– 5); b) A(4; 2; –1), B(1; –3; –2), C(–6; 2; 1); c) A(– 1; 7; 4), B(1; 5; 2), C(9; –3; – 8) bo‘lsa, D uchining koordinatalarini toping.
33. CK kesmani CK:KM =
λ nisbatda bo‘luvchi M(x; y; z) nuqtaning
koordinatalarini toping. a) C(–5; 4; 2), K(1; 1;–1) va λ=2;
b) C(1; –1; 2), K (2; –4; 1) va λ=0,5; c) C (1; 0;
–2), K (9; –3; 6) va ![]() .
.
34. Uchlari A(3; 2; 4), B(1; 3; 2), C(–3; 4; 3) nuqtalarda bo‘lgan uchburchak medianalari kesishish nuqtasi M ning koordinatalarini toping.
35. Uchlari A(5; 6; 3), B(3; 5; 1), C(0; 1; 1) nuqtalarda bo‘lgan uchburchakning BL bissektrisasining L uchi koordinatalarini toping.
36*.Uchlari A(4; 0; 1), B(5; –2; 1), C(4; 8; 5) nuqtalarda bo‘lgan uchburchakning AL bissektrisasi uzunligini toping.
37*.Uchlari A(1; 3; –1), B(3; –1; 1), C(3; 1; –1) nuqtalar bo‘lgan uchburchak berilgan. Uning: a) katta tomoniga tushirilgan balandligini; b) burchaklarini; c) yuzini toping.
38*.16- rasmda tasvirlangan kub haqidagi ma’lumotlardan foydalanib MK kesma uzunligini toping.
Abu Rayhon Beruniy mashhur tabib va matematik Abu Ali ibn Sino bilan yozishmalarida unga quyidagi savolni beradi: ,,Nima uchun Aristotel va boshqa (faylasuf)lar tomonlarni oltita deb atashadi?”
Beruniy olti yoqli kubni olib, ,,boshqacha sondagi tomonlarga ega bo‘lgan” jismlar haqida gapiradi va ,,sharsimon jismning tomonlari yo‘qligi”ni qo‘shib qo‘yadi.
Ibn Sino esa ,,hamma hollarda ham tomonlar oltita deb hisoblamoq zarur, chunki har bir jismda, uning shaklidan qat’iy nazar uch o‘lchov — uzunlik, chuqurlik va kenglik mavjud” deb javob beradi.
Bu yerda Ibn Sino ,,olti tomon” deb ishoralari bilan olingan uchta koordinatani nazarda tutadi.
Beruniy ,,Qonuniy Mas’udiy” asarida olti tomonning aniq matematik ma’nosini keltiradi: ,,Tomonlar oltita, chunki ular jismlarning o‘lchovlari bo‘yicha harakatlari chegarasidir. O‘lchovlar uchta, bu uzunlik, kenglik va chuqurlik, ularning uchlari esa o‘lchovlardan ikki marta ko‘p”.
Asarning oldingi kitoblarida muallif yoritgichlarning osmondagi holatini osmon sferasiga nisbatan ikki koordinata – ekliptik kenglama va uzoqlama orqali yoki xuddi shunday koordinatalar orqali, ammo osmon ekvatori yoki gorizontga nisbatan aniqlaydi. Ammo yulduzlar va yoritgichlarning o‘zaro joylashuvini aniqlash masalasida ularning bir-birlarini to‘sib qolish hollarini ham e’tiborga olishga to‘g‘ri keladi. Mana shunday holda uchinchi sferik koordinataga ehtiyoj tug‘iladi.Ana shu ehtiyoj Abu Rayhon Beruniyni fazoviy koordinatalar g‘oyasini ilgari surishga olib kelgan.
2. FAZODA VEKTORLAR VA ULAR USTIDA AMALLAR
Fazoda vektor tushunchasi tekislikdagi singari kiritiladi.
Fazoda vektor deb yo‘naltirilgan kesmaga aytiladi.
Fazoda vektorlarga oid asosiy tushunchalar: vektorning uzunligi (moduli), vektorning yo‘nalishi, vektorlarning tengligi tekislikdagi singari ta’riflanadi.
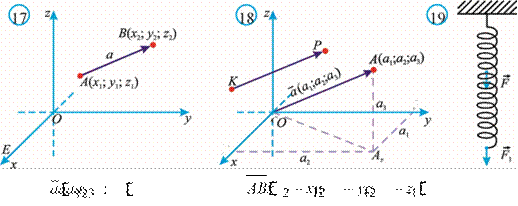
Boshi A (x1; y1; z1) nuqtada va oxiri B (x2; y2; z2) nuqtada bo‘lgan vektorning koordinatalari deb a1 = x2 – x1, a2 = y2 – y1, a3 = z2 – z1 sonlarga aytiladi (17- rasm).
Vektorlarning tekislikdagiga o‘xshash qator xossalari ham borki, ularni isbotsiz keltiramiz.
Xuddi tekislikdagi singari teng vektorlarning mos koordinatalari teng bo‘ladi va aksincha, mos koordinatalari teng bo‘lgan vektorlar teng bo‘ladi.
Bu vektorni uning koordinatalari bilan ifodalashga asos bo‘ladi. Vektor-
![]()
![]()
![]() lar AB
a a a 1
2 3; ; yoki a a a a
1
2 3; ; yoki qisqaroq (a1; a2; a3) tarzda belgilanadi (18-rasm).
lar AB
a a a 1
2 3; ; yoki a a a a
1
2 3; ; yoki qisqaroq (a1; a2; a3) tarzda belgilanadi (18-rasm).
![]()
![]() Vektor
koordinatalarisiz AB (yoki
qisqaroq a ) tarzda ham
belgilanadi. Bunda uning boshi birinchi o‘rinda, oxiri esa ikkinchi o‘rinda
yoziladi.
Vektor
koordinatalarisiz AB (yoki
qisqaroq a ) tarzda ham
belgilanadi. Bunda uning boshi birinchi o‘rinda, oxiri esa ikkinchi o‘rinda
yoziladi.
![]()
Koordinatalari nollardan iborat vektor nol vektor deb ataladi va 0 0 ;0;0
![]()
yoki 0 tarzda belgilanadi hamda bu vektorning yo‘nalishi bo‘lmaydi.
Agar O koordinata boshi va a1, a2 va a3 sonlar A nuqtaning koordinata-
![]()
lari, ya’ni A(a1; a2; a3) bo‘lsa, bu sonlar OA vektorning ham koordinatalari
![]()
bo‘ladi: OA(a1; a2; a3).
Lekin koordinatalar fazosida boshi K(c1; c2; c3) nuqtada, oxiri
![]()
P (c1+a1; c2+a2; c3+a3) nuqtada bo‘lgan KP vektor ham shu koordinatalar
![]()
bilan ifodalanadi: KP (c1+ a1– c1; c2+ a2– c2; c3+ a3– c3) = KP (a1; a2; a3).
Shundan kelib chiqib, vektorni koordinatalar fazosida istalgan nuqtaga qo‘yilgan qilib tasvirlash mumkin. Geometriyada biz shunday erkin vektorlar bilan ish ko‘ramiz. Fizikada esa, odatda, vektorlar biror nuqtaga qo‘yilgan bo‘ladi. Masalan, 19- rasmdagi F kuch prujinaning qaysi nuqtasiga qo‘yilgani bilan ahamiyatli hisoblanadi.
|
|
![]()
![]() a
(a1; a2; a3) vektorning uzunligi uning koordinatalari orqali |a
|= a1[6] +a22
+a32
formula bilan ifodalanadi.
a
(a1; a2; a3) vektorning uzunligi uning koordinatalari orqali |a
|= a1[6] +a22
+a32
formula bilan ifodalanadi.
1- masala. A(2; 7; –3), B(1; 0; 3), C(–3; – 4; 5) va D(–2; 3; –1) nuqta-
![]()
lar berilgan. AB BC, ,DC, AD AD, va BD vektorlardan qaysilari o‘zaro teng bo‘ladi?
Yechish: Teng vektorlarning mos koordinatalari teng bo‘ladi. Shuning uchun vektorlarning koordinatalarini topamiz:
![]() AB = (1 – 2, 0 – 7, 3 – (–3)) = (–1, –7, 6);
AB = (1 – 2, 0 – 7, 3 – (–3)) = (–1, –7, 6);
DC = ( – 3 – (–2), – 4 – 3, 5 – (–1)) = (–1, –7, 6).
Demak, AB = DC
. BC AD ekanligini mustaqil ko‘rsating. ![]()
Vektorlar yig‘indisining xossalari.
![]()
Ixtiyoriy a , b va c vektorlar uchun quyidagi xossalar o‘rinli:
|
a) a + b = b +a – vektorlarni qo‘shishning o‘rin almashtirish qonuni;
b) a + (b + c) = (a +b )+c – vektorlarni qo‘shishning taqsimot qonuni. |
Vektorlarni qo‘shishning uchburchak qoidasi.
![]()
Ixtiyoriy A, B va C nuqtalar uchun (21-rasm): ABBC AC.
Vektorlarni qo‘shishning parallelogramm qoidasi.
![]()
Agar ABCD – parallelogramm (22- rasm) bo‘lsa, ABAD AC .
Vektorlarni qo‘shishning ko‘pburchak qoidasi.
Agar A, B, C, D va E nuqtalar ko‘pburchak uchlari bo‘lsa (23- rasm),
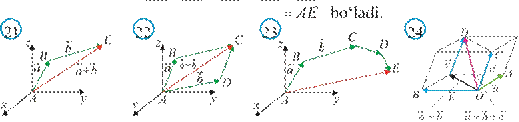 AB+BC+CD+DE
AB+BC+CD+DE
Bir tekislikda yotmagan uchta vektorlarni qo‘shishning parallelepiped qoidasi. Agar ABCDA1B1C1D1 parallelepiped (24- rasm) bo‘lsa,
![]()
AB + AD + AA 1 = AC bo‘ladi.
|
|
|
Ixtiyoriy a va b vektorlar hamda λ va μ sonlar uchun a) λ(a + b ) = λa +λb ; b) (λ+μ)a= λa +μa; c) |
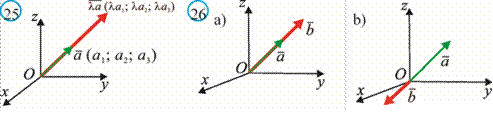
![]()
Nol vektordan farqli a va b vektorlar berilgan bo‘lsin. a va b vektorlar bir xil yoki qarama-qarshi yo‘nalgan bo‘lsa, ular kollinear vektorlar deb ataladi (26- rasm).
1- xossa. a va b vektorlar uchun a =λb (λ≠ 0) tenglik o‘rinli bo‘lsa, ular o‘zaro kollinear bo‘ladi va aksincha.
![]()
![]() Agar
λ> 0 bo‘lsa, a va b vektorlar bir tomonga (a ↑↑ b ), agar λ< 0 bo‘lsa, qarama-qarshi tomonga (a↑↓b ) yo‘nalgan bo‘ladi.
Agar
λ> 0 bo‘lsa, a va b vektorlar bir tomonga (a ↑↑ b ), agar λ< 0 bo‘lsa, qarama-qarshi tomonga (a↑↓b ) yo‘nalgan bo‘ladi.
|
2- xossa. a(a1; a2; a3) va b (b1; b2; b3) vektorlar o‘zaro kollinear bo‘lsa, ularning koordinatalari o‘zaro proporsional bo‘ladi: 1 a2 a3 va aksin- a b1 b2 b3 cha. |
2- masala. Boshi A (1; 1; 1) nuqtada va oxiri Oxy tekislikdagi B nuqtada
![]()
bo‘lgan va a(1; 2; 3) vektorga kollinear vektorni toping.
Yechish: B nuqtaning koordinatalari B(x; y; z) bo‘lsin. B nuqta Oxy
![]()
tekislikda yotgani uchun z=0. Unda AB (x – 1; y – 1; – 1) bo‘ladi.
![]()
![]()
Shartga ko‘ra, AB (x – 1; y – 1; – 1) va a (1, 2, 3) vektorlar kollinear. Demak, ularning koordinatalari o‘zaro proportsional bo‘ladi.
x1 y1 1
![]() Bundan proporsiyalarni hosil qilamiz.
Bundan proporsiyalarni hosil qilamiz.
![]() Ulardan x y ekanligini topamiz.
Ulardan x y ekanligini topamiz.
3 3
![]()
1 2
1 2
Unda AB
; ![]() ;–1 bo‘ladi.
;–1 bo‘ladi.
3 3
Bitta tekislikda yoki parallel tekisliklarda yotuvchi vektorlar komplanar vektorlar deb ataladi (27- rasm).
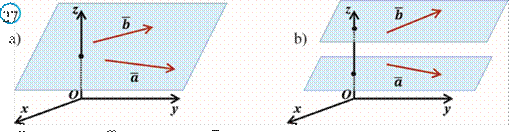
e1 (1; 0; 0), e2 (0; 1; 0) va e3 (0; 0; 1) vektorlar ortlar deb ataladi (28-
rasm).
![]()
![]()
![]()
![]() Ixtiyoriy a(a1; a2; a3) vektorni a= a1 e1 + a2 e2 + a3 e3 ko‘rinishda, yagona tarzda ortlar bo‘yicha yoyish mumkin
(29- rasm).
Ixtiyoriy a(a1; a2; a3) vektorni a= a1 e1 + a2 e2 + a3 e3 ko‘rinishda, yagona tarzda ortlar bo‘yicha yoyish mumkin
(29- rasm).
![]() Shuningdek, uchta komplanar bo‘lmagan
Shuningdek, uchta komplanar bo‘lmagan 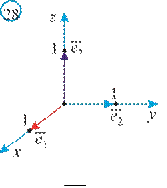 OA OB, va OC vektorlar
berilgan bo‘lsa, ixtiyoriy OD
vektorni quyidagi ko‘rinishda, yagona tarzda ifodalash mumkin:
OA OB, va OC vektorlar
berilgan bo‘lsa, ixtiyoriy OD
vektorni quyidagi ko‘rinishda, yagona tarzda ifodalash mumkin:
![]()
OD = a1∙ OA + a2 ∙ OB + a3 ∙ OC .
Bu yerda a1, a2, a3 qandaydir haqiqiy sonlar. Bunga vektorni berilgan vektorlar bo‘yicha yoyish deb ataladi.
|
nuqtadan chiquvchi OA= a vа OB= b vektorlarning yo‘naltiruvchi kesmalari orasidagi burchakka aytiladi (30- rasm). |
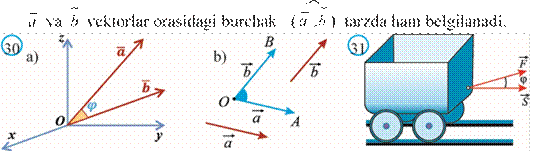
|
|
Agar vektorlarning biri nol vektor bo‘lsa, ularning skalar ko‘paytmasi nolga teng bo‘ladi.
Skаlar ko‘pаytmа a · b yoki (a ; b ) tarzda bеlgilаnаdi. Tа’rifgа ko‘rа
![]() (a
; b ) = |a
| ∙ |b |
cosφ. (1)
(a
; b ) = |a
| ∙ |b |
cosφ. (1)
Ta’rifdan ko‘rinadiki, a vа b vеktоrlаrning skаlar ko‘pаytmаsi nolga teng bo‘lsa, ular perpendikular bo‘ladi va aksincha.
![]()
![]() Fizikada
jismni F kuch ta’siri ostida s masofaga siljitishda bajarilgan A ish (31- rasm) F va s
vektorlarning skalar ko‘paytmasiga teng bo‘ladi:
Fizikada
jismni F kuch ta’siri ostida s masofaga siljitishda bajarilgan A ish (31- rasm) F va s
vektorlarning skalar ko‘paytmasiga teng bo‘ladi:
![]()
A = ( F , s ) =| F | ∙ |s | cosφ.
|
|
![]()
![]()
![]()
![]()
![]() Isbot. a va b
vektorlarni koordinata boshi O nuqtaga qo‘yamiz (32- rasm). Unda
Isbot. a va b
vektorlarni koordinata boshi O nuqtaga qo‘yamiz (32- rasm). Unda
OA = (a1; a2; a3) va OB = (b1; b2; b3) bo‘ladi. Agar berilgan vektorlar kollinear bo‘lmasa, ABO uchburchakdan iborat bo‘ladi va uning uchun kosinuslar teoremasi o‘rinli bo‘ladi:
AB2 OA2 OB2 2OA OB c cosφ. Unda
![]() 1 2 2 2 2 2 2 2 ,
1 2 2 2 2 2 2 2 ,
OA OB⋅ ⋅cosϕ = (OA OB AB+ − ) bo'ladi. Lekin, OA a1 a2 a3
OB![]() . va AB2
(b1 a1)2
(b2 a2)2
(b3 a3)2
.
. va AB2
(b1 a1)2
(b2 a2)2
(b3 a3)2
.
![]() Demak, (a ,b
) =|a |∙|b
|cosφ =
Demak, (a ,b
) =|a |∙|b
|cosφ = ![]() (OA2
OB2
–
AB2)
(OA2
OB2
–
AB2)
![]() 1 2 2 2 2 2 2 2
– (b2 a2)2
–
1 2 2 2 2 2 2 2
– (b2 a2)2
–
(a1 a2 a3 b1 b2 b3 (b1 a1)
2
– (b3 a3) )2 a b1 1a b2 2 a b3 3 .
Berilgan vektorlar
kollinear bo‘lgan (φ=0°, φ=180°) holda ham bu tenglik o‘rinli
bo‘lishini mustaqil ko‘rsating.![]()
Vektorlarning skalar ko‘paytmasining xossalari
|
1. 2. (a+b ) · c = a · c + b · c – taqsimot xossasi. 3. λ⋅(a⋅b) = (λ⋅a)⋅b = a⋅(λ⋅b) – guruhlash xossasi. 4. Agar a va b vektorlar bir xil yo‘nalishdagi kollinear vektorlar bo‘lsa,
a · b = |a| |b | bo‘ladi, chunki cos 0° = 1.
5. Agar qarama-qarshi yo‘nalgan bo‘lsa, a · b = –| a | |b |, chunki cos180° = –1.
6.
7. a vektor b vektorga perpendikular bo‘lsa, a · b = 0 bo‘ladi. |
Nаtijаlаr:

c) a = (a1;a2;a3 ) vа b = (b1;b2;b3 ) vеktоrlаrning pеrpеndikularlik shаrti: a1b1+a2b2+a3b3=0. (3)
3- masala. A(0; 1; –1), B(1; –1; 2), C(3; 1; 0), D(2; –3; 1) nuqtalar berilgan. AB va CD vektorlar orasidagi burchakning kosinusini toping.
![]() Yechish. AB va CD
vektorlarning koordinatalarini so‘ng uzunliklarini topamiz: AB = (1 – 0; –1 – 1; 2 – (–1)) = ( 1, –2, 3),
Yechish. AB va CD
vektorlarning koordinatalarini so‘ng uzunliklarini topamiz: AB = (1 – 0; –1 – 1; 2 – (–1)) = ( 1, –2, 3),
CD = ( 2 – 3; – 3 – 1; 1 – 0) = ( –1, –4, 1).
CD ( 1)2 ( 4)2 12 18.
AB CD 1 ( 1) ( 2)( 4) 3 1 5
![]() Demak, cosj .
Demak, cosj .
ABCD 14 18 63
4- masala. a(1;2;0), b(1;− ;0) vеktоrlаr orasidagi burchаkni toping.
a b⋅
Yechish: cosϕ = = a ⋅ b
1
1 1⋅ + 2− 2 + 0 0⋅ = 0 = 0.
1 2 5
2 2 2 2 2 5
1 + 2 + 0 1 + − 2 + 0 4
Demak, φ = 90°.
![]() 5- masala. |a |=3, |b |=5 va bu vektorlar orasidagi burchak ga teng bo‘lsa, |a + b
| ni toping.
5- masala. |a |=3, |b |=5 va bu vektorlar orasidagi burchak ga teng bo‘lsa, |a + b
| ni toping.
2 2 2 2 2
Yechish: a b ab a 2a b b a 2 a b cos b
1
9+25+2 15 34 15 19 2
6- masala. Agar a =2 i +3 j –4k va b =– i – j +2k bo‘lsa,
1) c =a+b; 2) d =2a – b vektorning koordinatalarini va uzunligini toping.
Yechish: a va b vektorlar yoyilmalarini koordinatalari izlanayotgan vektor ifodasiga qo‘yamiz: 1) c = a + b = 2i+3j– 4k–i–j+2k =i+2j–2k.
Demak, c =1;2;2. Unda |c| = 12 + 22 + (−2)2 = 3;
2) ![]() d = 2a – b = 2(2i + 3j – 4k) – ( –i – j +
2k ) = 4i + 6j – 8k+ i + j2k =
= 5i +7j – 10k.
d = 2a – b = 2(2i + 3j – 4k) – ( –i – j +
2k ) = 4i + 6j – 8k+ i + j2k =
= 5i +7j – 10k.
![]() Demak, d = 5;7;10. Unda d 52 72(10)2 174.
Demak, d = 5;7;10. Unda d 52 72(10)2 174.
![]()
![]() 7- masala. a va b vektorlar orasidagi burchak 30° ga teng va |a|
= 3
,
7- masala. a va b vektorlar orasidagi burchak 30° ga teng va |a|
= 3
,
|b|=2 bo‘lsa, (2a + 3b)(–2a+b) ko‘paytmani hisoblang.
Yechish: Avval a va b vektorlar ko‘paytmasini hisoblaymiz:
(a, b) =
|a||b| cos30° ![]() .
.
So‘ng vektorlar ko‘paytmasining taqsimot xossasiga ko‘ra, berilgan vektorlar ifodalarini ko‘phadni ko‘phadga ko‘paytirish kabi ko‘paytiramiz:
![]() (2a+3b)(–2a+b)=–4a2 +2(a, b)–6(a,
b)+3b2 =–4b2 – 4(a, b)+3b2.
(2a+3b)(–2a+b)=–4a2 +2(a, b)–6(a,
b)+3b2 =–4b2 – 4(a, b)+3b2.
a2=|a|2=9, b=|b|2 =4, (a, b)=3 ekanligini hisobga olsak, izlanayotgan
ko‘paytma (2a+3b)(–2a+b)=–4∙9–4∙3+3∙4=–36.![]()
39. 33- rasmdagi vektorlarning koordinatalarini aniqlang.
40. ![]()
![]()
![]()
![]()
![]() A(1; 1; 1), B(–1; 0;
1), C(0; 1; 1) va O(0; 0; 0) nuqtalar berilgan.
A(1; 1; 1), B(–1; 0;
1), C(0; 1; 1) va O(0; 0; 0) nuqtalar berilgan.
OA OB OC BO CO, , , , va AB vektorlar koordinatalarini aniqlang.
41.
42. Agar a) A(1; 2; 3), B(3; 7; 6); b) A(–3; 2; 1),
B(1; –4; 3) bo‘lsa, AB vektor koordinatalarini toping.
![]()
![]()
43. a (1; –1; 1), b (0; 2; –4), c(2; 3; –1), d (1; 2; 5) vektorlarning uzunligini toping.
![]()
44. ![]() Agar a
(2; 1; 3) va b (–1;
x; 2) vektorlar uzunligi teng bo‘lsa, x ni toping.
Agar a
(2; 1; 3) va b (–1;
x; 2) vektorlar uzunligi teng bo‘lsa, x ni toping.
![]()
45. Uzunligi 54 ga teng bo‘lgan a (c; 2c; –c) vektorning koordinatalarini toping.
46. A, B, C, D, E va F nuqtalar muntazam oltiburchakning uchlari bo‘lsa, ular orqali: a) ikkita teng; b) ikkita bir xil yo‘nalgan; c) ikkita qaramaqarshi yo‘nalgan va teng; d) ikkita qarama-qarshi yo‘nalgan va teng bo‘lmagan vektorlarga misol keltiring.
![]()
47. ![]() k ning qanday qiymatida: a) a (4; k; 2); b) a (k–1;1;4); c) a (k; 1; k+2);
k ning qanday qiymatida: a) a (4; k; 2); b) a (k–1;1;4); c) a (k; 1; k+2);
![]()
d) a (k–1; k–2; k+1) vektorning uzunligi 21 ga teng bo‘ladi?
48. Uchta nuqta berilgan: A(1; 1; 1), B(–1; 0; 1), C(0; 1; 1). Shunday
![]()
D(x; y; z) nuqtani topingki, AB va CD vektorlar teng bo‘lsin.
![]()
49. Uchta nuqta berilgan: A(1; 0; 1), B(–1; 1; 2), C(0; 2; –1). Agar a) AB va
![]()
CD vektorlar teng; b) AB va CD vektorlarning yig‘indisi nol vektorga teng bo‘lsa, D (x; y; z) nuqtani toping.
50*. (2; n; 3) va (3; 2; m) vektorlar berilgan. m va n ning qanday qiymatlarida bu vektorlar kollinear bo‘ladi?
51. Boshi A(1; 1; 1) nuqtada va oxiri Oxy tekislikdagi B nuqtada bo‘lgan hamda a(1;–2; 3) vektorga kollinear vektorni toping.
52*. ABCD parallelogrammning uchlari a) A(–2; –4; 3), B (3; 1; 7), C (4; 2; –5); b) A(4; 2; –1), B(1; –3; –2), C(–6; 2; 1); c) A(–1; 7; 4), B(1; 5; 2), C(9; –3; –8); d) A(–2; –4; 3), B(3; 1; 7), C(4; 2; –5) bo‘lsa, D uchining koordinatalarini toping.
53. 34- rasmda tasvirlangan vektorlarning parallelepiped qoidasiga ko‘ra yig‘indisini toping.
54. Agar A(6;7;8), B(8;2;6), C(4;3;2), D(2;8; 4) va M(3; 5; 2), N(7; 1;2), P(3;–3;2), K(–1;1;2) bo‘lsa, ABCD va MNPK to‘rtburchaklardan qaysi biri romb, qaysinisi kvadrat bo‘ladi?
![]()
55. 35- rasmda tasvirlangan ABCDA1B1C1D1 kubda: a) AB, DD1, AC vektorlarga teng; b) A1D1, CC1, BD vektorlarga qarama-qarshi yo‘nalgan;
![]() c)BA, AA1, vektorlarga kollinear; d) AB va AD, AC va A1C vektorlar juftiga komplanar vektorlarni aniqlang.
c)BA, AA1, vektorlarga kollinear; d) AB va AD, AC va A1C vektorlar juftiga komplanar vektorlarni aniqlang.
![]()
56. ![]() Agar 1) a(1;– 4;0), b(– 4;0;8); 2) a(0;2;5),
b(4; 3; 0) bo‘lsa, c = a + b vektorning
koordinatalarini va uzunligini toping.
Agar 1) a(1;– 4;0), b(– 4;0;8); 2) a(0;2;5),
b(4; 3; 0) bo‘lsa, c = a + b vektorning
koordinatalarini va uzunligini toping.
![]()
57. ![]() Agar 1) a(1;
–4; 0), b(–4; 8; 0); 2) a(0; –2; 7), b(0; 4; –1) bo‘lsa, c
= a – b vektorning koordinatalarini va uzunligini toping.
Agar 1) a(1;
–4; 0), b(–4; 8; 0); 2) a(0; –2; 7), b(0; 4; –1) bo‘lsa, c
= a – b vektorning koordinatalarini va uzunligini toping.
![]()
58. Agar b(– 4; 8; 2) bo‘lsa, a) 2b; b) –3 b; c) –1,5 c; d) 0 ∙ b vektorning koordinatalarini va uzunligini toping.
![]()
59. a(1; –1; 1), b(0; 2; –4), c(2; 3; –1), d(1; 2; 5) vektorlarni ortlar bo‘yicha yoying.
![]()
![]() 60*.
a(1; –1; 1), b (0; 2; –4), c(2; 3;
–1), d(1; 2; 5) vektorlar berilgan. |a + 2b|, |a – 3b|, |c – 2d|,
|3a + 4d|
ni toping.
60*.
a(1; –1; 1), b (0; 2; –4), c(2; 3;
–1), d(1; 2; 5) vektorlar berilgan. |a + 2b|, |a – 3b|, |c – 2d|,
|3a + 4d|
ni toping.
61*. K va P nuqtalar ayqash to‘g‘ri chiziqlarda yotuvchi AB
va CD kesmalarning o‘rtasi hamda O nuqta KP kesmaning
o‘rtasi bo‘lsa (36-rasm),  OA + OB + OC + OD
OA + OB + OC + OD
62. 37- rasmda OA1 = 2, OA2 = 2, OA3 = 3. a, b va A3A vektorlarning koordinatalarini aniqlang.
63. 38- rasmda ОА = 4, ОВ = 9, ОС = 2, M, N va P nuqtalar, mos ravishda,
![]()
AC, OC va CB kesmalarning o‘rtasi. AC, CB, AB, PC, MC va CN vektorlarning koordinatalarini toping.
64. Q nuqta PABC tetraedrning BC qirrasining o‘rtasi va O nuqta esa AQ
![]()
kesma o‘rtasi bo‘lsa (39- rasm), PO vektorni PAa, PB = b va
![]()
PC = c vektorlar orqali ifodalang.
![]()
65*. 40- rasmda tasvirlangan qayiqqa daryo oqimi F1 = 120 N kuch bilan va
![]()
qirg‘oqdan esayotgan shamol F2 = 100 N kuch bilan ta’sir qilmoqda. Qayiqning daryoda joyidan qo‘zg‘almay turishi uchun uni qanday kuch bilan ushlab turish kerak?

birlik vektorlar orasidagi burchakni toping.
![]()
67. ![]()
![]() a) a (1; –1; 1), b (0; 2; –4); b) c(2;
3; –1), d (1; 2; 5); c) e(1; –1; 1), f(0; 2; –
4); d) g(2; 3;–1), h(1; 2; 5) vektorlarning skalar ko‘paytmasini
toping.
a) a (1; –1; 1), b (0; 2; –4); b) c(2;
3; –1), d (1; 2; 5); c) e(1; –1; 1), f(0; 2; –
4); d) g(2; 3;–1), h(1; 2; 5) vektorlarning skalar ko‘paytmasini
toping.
![]()
68. ABC uchburchakda ∠A= 50°, ∠C= 90°. a) BA va BC; b) CA va AB;
c) ![]() AB va BA vektorlar orasidagi burchakni toping.
AB va BA vektorlar orasidagi burchakni toping.
69. ![]() a va b vektorlarning
uzunliklari va ular orasidagi burchak mos ravishda a) 5, 12, 50°; b) 3, 2,
45°; c) 5, 6, 120°; d) 4, 7, 180° bo‘lsa, ularning skalar ko‘paytmasini
toping.
a va b vektorlarning
uzunliklari va ular orasidagi burchak mos ravishda a) 5, 12, 50°; b) 3, 2,
45°; c) 5, 6, 120°; d) 4, 7, 180° bo‘lsa, ularning skalar ko‘paytmasini
toping.
70. n ning qanday qiymatida vektorlar perpendikular bo‘ladi?
![]()
![]() a) a(2; –1; 3), b(1;
3; n); b) a(n; –2; 1), b(n; –n;
1);
a) a(2; –1; 3), b(1;
3; n); b) a(n; –2; 1), b(n; –n;
1);
c) a(n; –2; 1), b(n; 2n; 4); d) a(4; 2n; –1), b(–1; 1; n).
71. ![]() a(1;–5;2), b(3;1;2)
vektorlar berilgan. a) a +b va a – b; b) a+2b va 3a – b; c)
2a + b va 3a – 2b vektorlar skalar ko‘paytmasini toping.
a(1;–5;2), b(3;1;2)
vektorlar berilgan. a) a +b va a – b; b) a+2b va 3a – b; c)
2a + b va 3a – 2b vektorlar skalar ko‘paytmasini toping.
72. A (1; 0; 1), B (–1; 1; 2), C (0; 2; –1) nuqtalar berilgan. Oz koordinatalar
![]()
o‘qida shunday D nuqtani topingki, AB va CD vektorlar perpendikular bo‘lsin.
![]()
73*. (a, b) ≤ |a| ∙ |b| ekanligini asoslang. Bu vektorlar qanday bo‘lganda tenglik o‘rinli bo‘ladi?
![]()
75*. Uzunliklari birga teng a, b, c vektorlar juft-jufti bilan 60° li burchak tashkil etadi. a) a va b + a; b) a va b – c vektorlar orasidagi burchakni toping.
76. O nuqta ABCD kvadratning diagonallari kesishish nuqtasi. Kvadratning B uchidan diagonalga parallel va DA to‘g‘ri chiziq bilan F nuqtada kesi-
![]()
![]()
shadigan to‘g‘ri chiziq o‘tkazilgan. BF vektorni DO va DC vektorlar orqali ifodalang.
77. O nuqta ABC uchburchakning medianalari kesishish nuqtasi bo‘lsa,
![]()
![]()
OC vektorni AB va AC vektorlar bo‘yicha yoying.
78*. C nuqta AB kesmaning o‘rtasi bo‘lsa (42- rasm), unda ixtiyoriy M nuqta
![]() uchun MC=
uchun MC= ![]() (MA+MB) bo‘lishini isbotlang.
(MA+MB) bo‘lishini isbotlang.
79. K nuqta ABCD tetraedr BC qirrasining o‘rtasi bo‘lsa (43- rasm), DK
![]()
vektorni AB ,AD va AC vektorlar bo‘yicha yoying.
80*. Jismning siljish yo‘nalishiga nisbatan 30° li burchak ostida qo‘yilgan
![]()
F=20N kuch ta’sirida jism 3 m ga siljidi. Bu holatda bajarilgan ishni toping.
![]() 81*.
81*. Jismning siljish yo‘nalishiga nisbatan 60° li burchak ostida
qo‘yilgan F =50 N kuch ta’sirida jism 8 m ga siljidi. Bu holatda
bajarilgan ishni toping.
Jismning siljish yo‘nalishiga nisbatan 60° li burchak ostida
qo‘yilgan F =50 N kuch ta’sirida jism 8 m ga siljidi. Bu holatda
bajarilgan ishni toping.
82*. (Koshi – Bunyakovskiy tengsizligi) Ixtiyoriy a1, a2, a3, b1, b2, b3 sonlari uchun (a1b1 + a2b2 + a3b3)2 ≤ (a12 + a22 + a32) (b12 + b22 + b32) tengsizlikning o‘rinli bo‘lishini vektorlardan foydalanib isbotlang.
3. FAZODA ALMASHTIRISHLAR VA O‘XSHASHLIK
Fazoda berilgan F shaklning har bir nuqtasi biror bir usulda ko‘chirilsa, yangi F1 shakl hosil bo‘ladi. Agar bu ko‘chirishda (akslantirishda) birinchi shaklning har xil nuqtalari ikkinchi shaklning har xil nuqtalariga ko‘chsa, bu ko‘chishga geometrik shakl almashtirish deb ataladi.
Butun fazoni ham geometrik shakl sifatida qarasak, fazoviy shakl almashtirish haqida ham gapirish mumkin.
Ko‘rib turganingizdek, fazoda geometrik almashtirishlar tushunchasi tekislikdagi kabi kiritiladi. Shuningdek, uning quyida ko‘riladigan qator turlarining xossalari va ularning isboti ham tekislikdagisiga o‘xshash. Shu bois, bu xossalarning isbotiga to‘xtalmaymiz va ularni mustaqil bajar ishni tavsiya qilamiz.
|
Nuqtalar orasidagi masofani saqlaydigan shakl almashtirishlar harakat deb ataladi. Harakatning quyidagi xossalarini keltirish mumkin. |
|
Harakatda to‘g‘ri chiziq to‘g‘ri chiziqqa, nur-nurga, kesma unga teng kesmaga, burchak unga teng burchakka, uchburchak unga teng uchburchakka, tekislik unga teng tekislikka va tetraedr unga teng tetraedrga ko‘chadi (akslanadi). |
|
Fazoda biror harakat yordamida birini ikkinchisiga ko‘chirish mumkin bo‘lgan shakllar teng shakllar deyiladi. |
Harakatga eng sodda misol bu parallel ko‘chirishdir.
|
Fazoda biror KP vektor va ixtiyoriy X nuqta berilgan bo‘lsin (44-
rasm). Agar X1 nuqta XX1= KP shartni qanoatlantirsa, X nuqta X1 nuqtaga
KP vektor bo‘ylab parallel ko‘chirilgan deb ataladi. |
Agar fazoda berilgan F shaklning har bir nuqtasi KP vektor bo‘ylab ko‘chirilsa (45- rasm), yangi F1 shakl hosil bo‘ladi. Bu holda F shakl F1 shaklga parallel ko‘chirilgan deyiladi. Parallel ko‘chirishda F shaklning har bir nuqtasi bir xil yo‘nalishda bir xil masofaga ko‘chirilgan bo‘ladi.
46- rasmda tasvirlangan ko‘tarma kranning har bir nuqtasi boshlang‘ich holatiga nisbatan 40 m ga parallel ko‘chgan.
Ravshanki, parallel ko‘chirish harakatdir. Shuning uchun, parallel ko‘chirishda to‘g‘ri chiziq to‘g‘ri chiziqqa, nur nurga, tekislik tekislikka, kesma unga teng kesmaga ko‘chadi va hokazo.
![]()
Aytaylik KP = (a; b; c) vektor bo‘ylab parallel ko‘chirishda F shaklning X (x; y; z) nuqtasi F1 shaklning X1(x1; y1; z1) nuqtasiga o‘tsin. Unda, ta’rifga ko‘ra, quyidagilarga egamiz:
x1 – x = a, y1 – y = b, z1 – z = c yoki x1 = x + a, y1 = y + b, z1 = z + c.
![]() Bu tengliklar parallel ko‘chirish formulalari deb
ataladi.
Bu tengliklar parallel ko‘chirish formulalari deb
ataladi.
![]()
1- masala. p = (3; 2; 5) vektor bo‘ylab parallel ko‘chirishda P (–2; 4; 6) nuqta qaysi nuqtaga ko‘chadi?
Yechish.Yuqoridagi parallel ko‘chirish formulalardan foydalanamiz: x1 = –2 + 3 =1, y1 = 4+ 2 = 6, z1 = 6 +5 =11. Javob: P1(1; 6; 11).
Fazoda berilgan A va A1 nuqtalar O nuqtaga nisbatan simmetrik deyiladi,
![]()
agar AO = OA1 bo‘lsa, ya’ni O nuqta AA1 kesmaning o‘rtasi bo‘lsa.
Agar fazoda berilgan F shaklning har bir nuqtasi O nuqtaga nisbatan simmetrik nuqtaga ko‘chsa (47- rasm), bunday almashtirishga O nuqtaga nisbatan simmetriya deb ataladi. 48, 49- rasmlarda O nuqtaga nisbatan simmetrik shakllar tasvirlangan.
Nuqtaga nisbatan simmetriya – harakatdir.
Agar F shakl O nuqtaga nisbatan simmetrik almashtirishda o‘ziga ko‘chsa, bunday shaklga markaziy simmetrik shakl deb ataladi.

Masalan, parallelepiped (50- rasm) diagonallari kesishish nuqtasi O ga nisbatan markaziy simmetrik shakldir.
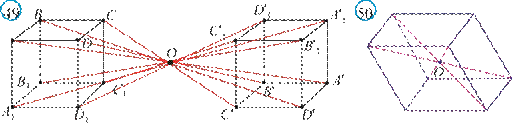
2- masala. O (2; 4; 6) nuqtaga nisbatan markaziy simmetriyada A = (1; 2; 3) nuqta qaysi nuqtaga o‘tadi?
Yechish. A1 = (x; y; z) izlanayotgan nuqta bo‘lsin. Ta’rifga ko‘ra, O nuqta
AA1 kesmaning o‘rtasi. Demak, 2
= x+1, 4 = y![]() +2, 6 = z+3.
+2, 6 = z+3.
2 2 2
Bu tengliklardan x =
4 – 1 = 3, y = 8 – 2 = 6, z =12 – 3 = 9. Javob: A1(3; 6; 9).![]()
Fazoda berilgan A va A1 nuqtalar tekislikka nisbatan simmetrik deyiladi, agar tekislik AA1 kesmaga perpendikular bo‘lib, uni teng ikkiga bo‘lsa
(51- rasm). 52- rasmda tekislikka nisbatan simmetrik bo‘lgan F1 va F2 shakllar keltirilgan. Ravshanki, gavdamiz va aksimiz oyna tekisligiga nisbatan simmetrik bo‘ladi (53- rasm).
Tekislikka nisbatan simmetriya – harakatdir.

Demak, tekislikka nisbatan simmetriyada kesma o‘ziga teng kesmaga, to‘g‘ri chiziq – to‘g‘ri chiziqqa va tekislik – tekislikka akslanadi.
Agar F shakl tekislikka nisbatan simmetrik almashtirishda o‘ziga ko‘chsa, bunday shaklga tekislikka nisbatan simmetrik shakl deyiladi.
Masalan, 54- rasmda tasvirlangan kub AA1va CC1 qirralaridan o‘tuvchi a tekislikka nisbatan simmetrik shakl bo‘ladi.

Agar fazoda berilgan F shaklning har bir nuqtasi l to‘g‘ri chiziqqa nisbatan φ burchakka bursak, yangi F1 shakl hosil bo‘ladi. Bunda F shakl l to‘g‘ri chiziqqa nisbatan φ burchakka burishda F1 shaklga o‘tdi deyiladi. 56- rasmda shunday burishdan hosil bo‘lgan shakllar ko‘rsatilgan.
Masalan, 57- rasmda tasvirlangan kubni l to‘g‘ri chiziqqa nisbatan 180° burchakka burishda yangi kubni hosil qilamiz.
|
To‘g‘ri chiziqqa nisbatan burish ham harakat bo‘ladi. |
|
l to‘g‘ri chiziqqa nisbatan 180° burchakka burish l to‘g‘ri chiziqqa nisbatan simmetriya deb ataladi. |
|
Shaklning simmetriya markazi, o‘qi, tekisligi uning simmetriya elementlari deb ataladi. |
A(x; y; z) nuqtaga koordinata tekisliklari, koordinata o‘qlari va koordinata boshiga nisbatan simmetrik nuqtalar quyidagi koordinatalarga ega bo‘ladi:
|
Simmetriya elementi |
Simmetrik nuqta koordinatalari |
|
Oxy tekislik |
(x; y; –z) |
|
Oxz tekislik |
(x; –y; z) |
|
Oyz tekislik |
(–x; y; z) |
|
Ox o‘qi |
(x; –y; –z) |
|
Oy o‘qi |
(–x; y; –z) |
|
Oz o‘qi |
(–x; –y; z) |
|
O nuqta |
(–x; –y; –z) |

Tabiatda simmetriyani har qadamda uchratish mumkin. Masalan, jonli mavjudodlarning ko‘pchiligi, xususan, inson va hayvonlar gavdasi, o‘simliklarning barglari va gullari simmetrik tuzilgan (58- rasm). Shuningdek, jonsiz tabiat unsurlari ham borki, maslan, qor zarralari, tuz kristallari, moddalarning molekular tuzilishi ham ajoyib simmetrik shakllardan iboratdir. Bu bejiz emas, albatta, chunki simmetrik shakllar chiroyli bo‘lishi bilan birga, qaysidir ma’noda eng maqbul va mukammal hisoblanadi. Shunday ekan, tabiatdagi go‘zallik va mukammallik simmetriya asosiga qurilgan, deb aytishimiz mumkin. Tabiatdagi bu go‘zallik va mukammallikdan andoza olgan quruvchi, mahandis va arxitektor kabi ijodkorlar yaratgan ko‘plab inshoot va binolar, qurilma va mexanizmlar, texnika va transport vositalari ham simmetrik yaratilgan. Bu ishda ularga geometriya fanining yordami beqiyosdir.

Ko‘rib turganingizdek, fazoda o‘xshashlik almashtirishi tushunchasi tekislikdagidek kiritiladi. Shuningdek, uning quyida ko‘riladigan qator turlari ta’rifi, ularning xossalari va bu xossalarning isboti ham tekislikdagisiga o‘xshash. Shu bois, bu xossalarning isbotiga to‘xtalmaymiz va ularni mustaqil bajarishni tavsiya qilamiz.
|
Fazodagi o‘xshashlik almashtirishi to‘g‘ri chiziqni to‘g‘ri chiziqqa, nurni nurga, kesmani kesmaga va burchakni burchakka akslantiradi. Shuningdek, bu almashtirish tekislikni ham tekislikka akslantiradi. |
|
Fazoda berilgan ikki shaklning biri ikkinchisiga o‘xshashlik almashtirishi orqali akslansa, ular o‘xshash shakllar deb ataladi. |
Fazoda F shakl, O nuqta va k noldan farqli (k≠0) son berilgan bo‘lsin.
|
F shaklning ixtiyoriy X nuqtasini OX1 =kOX shartni qanoatlantiruvchi X1 nuqtaga akslantiruvchi almashtirish O nuqtaga nisbatan k koeffitsiyentli gomotetiya deb ataladi (61-rasm). O nuqtaga gomotetiya markazi, k soniga esa gomotetiya koeffitsiyenti deyiladi. |
|
F shaklning har bir nuqtasi shu usulda akslantirilsa, natijada F1 shakl hosil bo‘ladi va bu gomotetiyada F shakl F1 shaklga akslanadi deyiladi. |
Ko‘rib turganingizdek, fazoda gomotetiya ta’rifi tekislikdagisi bilan deyarli bir xil. Shuningdek, uning qator xossalari ham borki, ular ham, ularning isbotlari ham tekislikdagisiga o‘xshash. Shu bois, bu xossalarning isbotiga to‘xtalmaymiz va ularni mustaqil bajarishni tavsiya qilamiz.
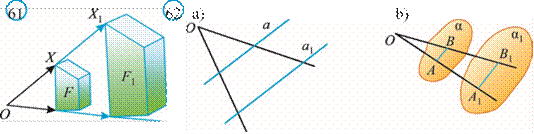
O nuqtaga nisbatan k koeffitsiyentli gomotetiya o‘xshashlik almashtirishidir.
Gomotetiya koeffitsiyenti k ixtiyoriy noldan farqli son bo‘lib, k=1 da F shakl o‘ziga o‘zi akslanadi, k=–1 da esa F shakl O nuqtaga nisbatan simmetrik F1 shaklga akslanadi. Boshqa hollarda gomotetiya nuqtalar orasidagi masofani saqlamaydi, ya’ni u harakat bo‘lmaydi. Gomotetiya natijasida nuqtalar orasidagi masofa bir xil k songa ko‘payadi, ya’ni shaklning o‘lchamlari o‘zgaradi, lekin uning shakli o‘zgarmaydi.
Gomotetiyada gomotetiya markazidan o‘tmaydigan a) to‘g‘ri chiziq unga parallel to‘g‘ri chiziqqa (62.a- rasm); b) tekislik esa unga parallel tekislikka akslanadi (62.b- rasm).
Gomotetiyada gomotetiya markazidan o‘tuvchi to‘g‘ri chiziq yoki tekislik o‘ziga o‘zi akslanadi.
83. p = (–2; 1; 4) vektor bo‘ylab parallel ko‘chirishda, a) (3; –2; 3);
b) (0; 2; –3); c) (2; –5; 0) nuqta qaysi nuqtaga ko‘chadi?
84. Parallel ko‘chirishda A(4; 2; –8) nuqta (3; 7; –5) nuqtaga ko‘chdi. Par allel ko‘chirish qaysi vektor bo‘ylab amalga oshirilgan?
85. Parallel ko‘chirishda: a) to‘g‘ri chiziq - to‘g‘ri chiziqqa; b) nur nurga;c) tekislik tekislikka; d) kesma unga teng kesmaga ko‘chishini isbotlang.
86. O (–2; 3; –1) nuqtaga nisbatan markaziy simmetriyada A (4; 2; –3) nuqta qaysi nuqtaga o‘tadi?
87. 63- rasmda tasvirlangan shakllarda O nuqta simmetriya markazi ekanligini asoslang.
88. (–2; 5; –9), (2; 2; –7), (–6; 12; –2) nuqtalar koordinata boshiga nisbatan markaziy simmetriyada qaysi nuqtalarga o‘tadi?
89*. Markaziy simmetriyaning harakat ekanligini isbotlang.

90*. Tekislikka nisbatan simmetriyaning harakat ekanligini isbotlang.
91. Parallelepipedning (50- rasm) diagonallari kesishish nuqtasi O ga nisbatan markaziy simmetrik shakl ekanligini isbotlang.
92. (1; 2; –3), (0; 2; –3), (2; 2; –3) nuqtalar koordinata tekisliklariga nisbatan simmetriyalarda qaysi nuqtalarga o‘tadi?
93. (2; 4; –1) nuqta koordinata tekisligiga nisbatan simmetrik akslantirishda (2; –4; –1) nuqtaga o‘tdi. Akslantirish qaysi koordinata tekisligiga nisbatan amalga oshirilgan?
94. Quyidagi jadvalda berilgan 1- namuna asosida bo‘sh kataklarni to‘ldiring.
|
№ |
Berilgan nuqta |
Simmetrik nuqta |
Nimaga nisbatan simmetrik? |
|
1 |
( 1; 2; 3) |
(1; 2; –3) |
Oxy tekislikka nisbatan |
|
2 |
( 2; 4; –1) |
|
Oxz tekislikka nisbatan |
|
3 |
|
( 1; 2; 3 ) |
Oyz tekislik |
|
4 |
(–1; –2; –3) |
(–1; 2; 3) |
|
|
5 |
(–1; 6; 3) |
|
Oy o‘qi |
|
6 |
|
(–3; 8; –2) |
Oz o‘qi |
|
7 |
(4; 1; –2) |
|
O nuqta |
95. 49- rasmda tasvirlangan shakllarda O nuqta simmetriya markazi ekanligini asoslang.
96*. To‘g‘ri chiziqqa nisbatan burish harakat ekanligini ko‘rsating.
97. O nuqtaga nisbatan k koeffitsiyentli gomotetiya o‘xshashlik almashtirishi ekanligini ko‘rsating.
98. Oxy tekislikka nisbatan simmetriyada ixtiyoriy (x; y; z) nuqta (x; y; –z) nuqtaga o‘tishini ko‘rsating.
99. Oxz tekislikka nisbatan simmetriyada ixtiyoriy (x; y; z) nuqta (x; –y; z) nuqtaga o‘tishini ko‘rsating,
100. Parallel ko‘chirishda (1; 2; –1) nuqta (1; –1; 0) nuqtaga o‘tdi. Koordinata boshi bu almashtirishda qaysi nuqtaga o‘tadi?
101. Parallel ko‘chirishda (3; 4; –1) nuqta (2; –4; 1) nuqtaga o‘tdi. Bu almashtirishda koordinata boshi qaysi nuqtaga o‘tadi?
102*. A(2; 1; 0) nuqta B (1; 0; 1) nuqtaga, C (3; –2; 1) nuqta esa D (2; –3; 0) nuqtaga o‘tadigan parallel ko‘chirish mavjudmi?
103*. A (–2; 3; 5) nuqta B (1; 2; 4) nuqtaga, C (4; –3; 6) nuqta esa D(7; –2; 5) nuqtaga o‘tadigan parallel ko‘chirish mavjudmi?
104. 58- rasmda tasvirlangan jonli va jonsiz obyektlar fazoviy jism sifatida qanday simmetrik shakl bo‘lishi mumkinligini aniqlang.Ularning (agar mavjud bo‘lsa) simmetriya markazi, simmetriya o‘qi yoki simmetriya tekisliklarini chizib ko‘rsating.
105. 60- rasmda tasvirlangan ona-bolalar (matreshkalar) ning katta ona mat-reshkaga nisbatan o‘xshashlik koeffitsiyentlarini aniqlang.
106. Muntazam tetraedr qirrasining uzunligi 12 cm ga teng. Bu tetraedrga:
a)
3; b) –4; c) ![]() ; d) –
; d) – ![]() ; koeffitsiyentli gomotetik bo‘lgan tetraedr qirrasining uzunligi
nimaga teng?
; koeffitsiyentli gomotetik bo‘lgan tetraedr qirrasining uzunligi
nimaga teng?
107. Ixtiyoriy ABC uchburchak chizing va biror O
nuqtani belgilang. Markazi O nuqtada va koeffitsiyenti: a) 2; b) –3; c)
– ![]() ; d)
; d) ![]() ga teng bo‘lgan gomotetiyada ABC uchburchak o‘tadigan
uchburchakni quring.
ga teng bo‘lgan gomotetiyada ABC uchburchak o‘tadigan
uchburchakni quring.
108. Ixtiyoriy SABC tetraedr chizing. Markazi S nuqtada va koeffitsiyenti:
a)
1,5; b) –2; c) ![]() ; d)
; d) ![]() ga teng bo‘lgan gomotetiyada SABC tetraedr o‘tadigan
tetraedrni quring.
ga teng bo‘lgan gomotetiyada SABC tetraedr o‘tadigan
tetraedrni quring.
109. Ixtiyoriy kub chizing. Markazi kubning biror uchida va koeffitsiyenti:
a)
2; b) –2; c) ![]() ; d) –
; d) – ![]() ga teng bo‘lgan gomotetiyada bu kub o‘tadigan fazoviy
geometrik shaklni quring.
ga teng bo‘lgan gomotetiyada bu kub o‘tadigan fazoviy
geometrik shaklni quring.
110. Markazi koordinata boshida va koeffitsiyenti: a) 2,5; b) –2,5;
c) ![]() ; d)
; d) ![]() ga teng bo‘lgan gomotetiyada A(–2; 3; 5) nuqta
o‘tadigan nuqtaning koordinatalarini toping.
ga teng bo‘lgan gomotetiyada A(–2; 3; 5) nuqta
o‘tadigan nuqtaning koordinatalarini toping.
111. Markazi O(–1;2;2) nuqtada va koeffitsiyenti: a) 0,5; b)
–2; c) ![]() ; d) –
; d) – ![]() ga teng bo‘lgan gomotetiyada A(2; 4; 0) nuqta
o‘tadigan nuqtaning koordinatalarini toping.
ga teng bo‘lgan gomotetiyada A(2; 4; 0) nuqta
o‘tadigan nuqtaning koordinatalarini toping.
112. Uchlari O(0; 0; 0), A(4; 0; 0), B(0; 4; 0), C(0; 0; 4) nuqtalarda bo‘lgan tetraedr: a) markazi O nuqtada, koeffitsiyenti –1 ga teng; b) markazi A nuqtada, koeffisiyenti 2 ga teng bo‘lgan gomotetiyada o‘tadigan tetraedrning uchlari koordinatalarini toping.
113*. Gomotetiyada uning markazidan o‘tmaydigan: a) to‘g‘ri chiziq o‘ziga parallel to‘g‘ri chiziqqa, b) tekislik esa o‘ziga parallel tekislikka akslanishini ko‘rsating.
114*. Gomotetiyada uning markazidan o‘tuvchi to‘g‘ri chiziq yoki tekislik o‘ziga o‘zi akslanishini ko‘rsating.
4. BOBNI TAKRORLASHGA DOIR AMALIY MASHQLAR
1. A(x1; y1; z1) va B(x2; y2; z2) nuqtalar berilgan. z2 – z1 nimani anglatadi?
A) AB kesma o‘rtasining koordinatasini; B) AB kesma uzunligini;
C) AB vektor uzunligini; D) AB vektor koordinatalaridan birini.
2. 64- rasmda AB⊥α, a⊂a, AO=OB bo‘lsa,
A) A va B nuqtalar O nuqtaga nisbatan simmetrik bo‘ladi;
B) A va B nuqtalar a to‘g‘ri chiziqqa nisbatan simmetrik bo‘ladi; C) A va B nuqtalar a tekislikka nisbatan simmetrik bo‘ladi;
D) AB kesma a to‘g‘ri chiziqqa nisbatan simmetrik bo‘ladi.
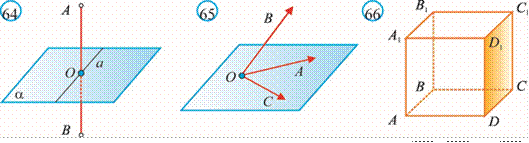
3. 65- rasmda B nuqta AOC tekislikda yotmaydi. Unda OA, OB va OC vektorlar …
A) kollinear; B) komplanar; C) bir xil yo‘nalishli; D) komplanar emas.
4. M(–7; 1; 4) va N(–1; –3; 0) nuqtalar berilgan. MN kesma o‘rtasining koordinatalarini toping.
A) (–4; –1; 4); B) (–4; –1;2); C) (–4; –2; 2); D) (–3; 2; 2).
5. A(0; –3; 2) va B(4; 0; –2) nuqtalar berilgan. AB kesma o‘rtasi nimaga tegishli?
A) Ox o‘qiga; B) Oy o‘qiga; C) Oz o‘qiga; D) Oxy tekisligiga.
6.
![]()
![]() A(3; 4; –3) nuqtadan Oz o‘qigacha bo‘lgan masofani toping.
A) 3; B) 5; C) 2 3; D) 34 .
A(3; 4; –3) nuqtadan Oz o‘qigacha bo‘lgan masofani toping.
A) 3; B) 5; C) 2 3; D) 34 .
7.
![]() CD+DE+EF
vektorlar yig‘indisini toping.
CD+DE+EF
vektorlar yig‘indisini toping.
A) O; B) CF; C) DF; D) CE.
8. m ning qaysi qiymatida a(m; 4; –3) va b(4; 8; –6) vektorlar kollinear bo‘ladi?
A) 2; B) 5; C) 1; D) 3.
9. O nuqta α tekislikda yotmaydi. Markazi O nuqtada bo‘lgan gomotetiyada α tekislik undan farqli bo‘lgan β tekislikka o‘tadi. Agar a to‘g‘ri chiziq α tekislikka tegishli bo‘lsa, …
A) α || β bo‘ladi; B) α tekislik β tekislik bilan kesishadi;
C) a ⊂ β bo‘ladi; D) α ⊥ β bo‘ladi.
10. AB to‘g‘ri chiziq BCD tekislikka perpendikular. Qaysi vektorlarning skalar ko‘paytmasi nolga teng bo‘ladi?
![]()
A) CA va CB; B) BD va AD; C) AC va BC; D) AB va CD.
11. Qirrasi 1 ga teng bo‘lgan ABCDA1B1C1D1 kub berilgan (66- rasm).
![]()
(AB+BC) ∙ BB ni toping.
A) 1; B) 0; C) –1; D) 0,5.
![]()
12. p ning qaysi qiymatida a(1; 1; 0) va b(0; 4; p) vektorlar orasidagi burchak 60° ga teng bo‘ladi?
A) 4; B) 4 yoki –4; C) 16; D) 16 yoki –16.
13. ABCDA1B1C1D1 kub berilgan. Parallel ko‘chirishda A1D kesma D1C kesmaga o‘tadi. Bu ko‘chirishda AA1B1 tekislik qaysi tekislikka o‘tadi? A) DB1B; B) DCC1; C) AA1C1; D) ABC.
14. a tekislik unda yotmaydigan ABC uchburchakning simmetriya tekisligidir. Qaysi tasdiq to‘g‘ri?
A) (ABC)![]() α;
B) ABC uchburchak teng yonli; C) ABC uchburchakning
simmetriya markazi bor;
α;
B) ABC uchburchak teng yonli; C) ABC uchburchakning
simmetriya markazi bor;
D) ABC uchburchakning simmetriya o‘qi bor.
15. ![]() ABCDA1B1C1D1 kub berilgan. A1B1+BC–DD1 ni toping.
ABCDA1B1C1D1 kub berilgan. A1B1+BC–DD1 ni toping.
![]()
A) A1C; B) BD1 ; c) B1D; D) AC1 .
16. Qaysi geometrik almashtirish ikki ayqash to‘g‘ri chiziqlardan birini ikkinchisiga o‘tkazadi?
A) parallel ko‘chirish; B) tekislikka nisbatan simmetriya;
C) burish; D) gomotetiya.
17. M(–1; 2; –4) nuqtaga Oyz tekislikka nisbatan simmetrik bo‘lgan nuqtani toping.
A) (1; –2; 4); B) (1; 2; –4); C) (–1; –2; –4); D) (–1; 2; 4).
![]()
18. Parallel ko‘chirishda AB vektor DC vektorga o‘tadi. Qaysi tasdiq noto‘g‘ri?
![]()
A) AB=DC; B) AC va BD kesma o‘rtalari ustma-ust tushadi; C) AB, AC va DC vektorlar komplanar; D) ABCD parallelogramm.
19. В(–3; 2; –5) nuqta Oxz tekislikdan qanday masofada yotibdi?
A) ![]() 2;
B) 5; C) 3; D) 34 .
2;
B) 5; C) 3; D) 34 .
20. А(1; –2; 0), В(1; –4; 2), С(3; 2; 0) nuqtalar ABC uchburchakning uchlari. CM mediana uzunligini toping.
![]()
A) ![]() 2√3; B) 3√2; C) 6
; D) 18.
2√3; B) 3√2; C) 6
; D) 18.
21. Agar a(1; m; 2) va b(0,5m+1; 3; 1) vektorlar kollinear bo‘lsa, m+n ni toping.
A) 3; B) 5; C) –4; D) 9.
22. А(–1; –9; –3) va В(0; –2; 1) nuqtalar berilgan. vektorni koordinata vektorlari (ortlar) bo‘yicha yoying.
![]()
A) (BA) = i+ 9j – k; B) (BA) = i – 9j+ k;
C) (BA) = –i – 9j – 4k; D) (BA) = i + 9j – 4k.
23. А(1; –2; 2), В(1; 4; 0), С(–4; 1; 1) va D(–5; –5; 3) nuqtalar berilgan. АС va ВD vektorlar orasidagi burchakni toping
A) 150°; B) 30°; C) 45°; D) 90°.
24. |a̅ | = 6, |a̅ +b̅ | =11, |a̅ –b̅ | = 7 ekanligi ma’lum bo‘lsa, |b̅ | ni toping.
A) 11; B) 18; C) 20 ; D) 7.
25. Asoslari ВС va АD bo‘lgan АВСD trapetsiya berilgan. Agar AB(–7; 4; 5), AC(3; 2; –1), AD(20; –4; –12), М va N – mos ravishda АВ va СD tomonlar o‘rtasi bo‘lsa, MN vektor koordinatalari yig‘indisini toping.
A) 1; B) 2 ; C) 3; D) 4.
115. Uchlari A(1; –2; 4) va B(3; –4; 2) nuqtalarda bo‘lgan kesma o‘rtasining koordinatalarini toping.
116. A(x; 0; 0) nuqta B(1; 2; 3) va C(–1; 3; 4) nuqtalardan teng uzoqlikdaligi ma’lum bo‘lsa, x ni toping.
117. Agar kesmaning bir uchi A(1; –5; 4), o‘rtasi C(4; –2; 3) nuqtada bo‘lsa, ikkinchi uchining koordinatalari qanday bo‘ladi?
118. Oxz tekisligiga nisbatan A(1; 2; 3) nuqtaga simmetrik bo‘lgan nuqtani toping.
119. Koordinatalar boshiga nisbatan A(1; 2; 3) nuqtaga simmetrik bo‘lgan nuqtani toping.
120. Oxy tekisligiga nisbatan (1; 2; 3) nuqtaga simmetrik bo‘lgan nuqtani toping.
121. Oy o‘qqa nisbatan (2; –3; 5) nuqtaga simmetrik bo‘lgan nuqtani toping.
122. Quyidagi nuqtalardan qaysi biri Oyz tekislikda yotadi?
A(2; –3; 0); B(2; 0; –5); C(1; 0; – 4); D(0; 9; –7); E(1; 0; 0).
123. Quyidagi nuqtalardan qaysi biri Oxz tekislikda yotadi:
A(– 4; 3; 0); B(0; –7; 0); C(2; 0; –8); D(2; –4; 6); E(0; – 4; 5)?
124. ![]() A(–3; 8; 3 33 ) nuqtadan Ox o‘qqacha bo‘lgan masofani toping.
A(–3; 8; 3 33 ) nuqtadan Ox o‘qqacha bo‘lgan masofani toping.
![]()
125. A(3; –2; 5) va B(–4; 5; –2) nuqtalar berilgan. AB vektorning koordinatalarini toping.
![]()
126. a(1; –2; 3) vektorning oxiri B(2; 0; 4) nuqta bo‘lsa, bu vektorning boshini toping.
![]()
127. B(0; 4; 2) nuqta a(2; –3; 1) vektorning oxiri bo‘lsa, bu vektor boshining koordinatalarini toping.
128. ![]() a(x; 1; 2) vektorning uzunligi 3 ga teng. x ning
qiymatini toping.
a(x; 1; 2) vektorning uzunligi 3 ga teng. x ning
qiymatini toping.
129. a(4; –12; z) vektorning moduli 13 ga teng. z ning qiymatini toping.
![]()
130. Agar a(6; 2; 1) va b(0; –1; 2) bo‘lsa, c= 2a–b vektorning uzunligini toping.
![]()
131. Agar p(2; 5; –1) va q(–2; 2) bo‘lsa, m= 4p+2q vektorning uzunligini toping.
132. ![]()
![]() a(2; –3; 4) va b(–2; –3; 1) vektorlarning skalar
ko‘paytmasini toping. 133. m(–1; 5; 3) va n(2; –2; 4) vektorlarning skalar
ko‘paytmasini toping.
a(2; –3; 4) va b(–2; –3; 1) vektorlarning skalar
ko‘paytmasini toping. 133. m(–1; 5; 3) va n(2; –2; 4) vektorlarning skalar
ko‘paytmasini toping.
![]()
134. m ning qanday qiymatida a(1; m; –2) va b(m; 3; –4) vektorlar perpendikular bo‘ladi?
135. ![]() n ning qanday qiymatida a(n;
–2; 1) va b(n; n; 1) vektorlar perpendikular bo‘ladi?
n ning qanday qiymatida a(n;
–2; 1) va b(n; n; 1) vektorlar perpendikular bo‘ladi?
136. m ning qanday qiymatida a = m i +3 j +4k va b=4 i +m j –7k vektorlar perpendikular bo‘ladi?
137. A(1; –2; 2), B(1; 4; 0), C(–4; 1; 1) va D(–5; –5; 3) nuqtalar berilgan.
![]()
AC va BD vektorlar orasidagi burchakni toping.
138. ![]()
![]() n ning qanday qiymatlarida a(2; n; 6) va b(1;
2; 3) vektorlar kollinear bo‘ladi?
n ning qanday qiymatlarida a(2; n; 6) va b(1;
2; 3) vektorlar kollinear bo‘ladi?
139. m ning qanday qiymatida a(2; 3; –4) va b(m; –6; 8) vektorlar parallel bo‘ladi?
![]()
140. ![]() m va n ning qanday qiymatida a(–1; m; 2) va b(–2;
–4; n) vektorlar kollinear bo‘ladi?
m va n ning qanday qiymatida a(–1; m; 2) va b(–2;
–4; n) vektorlar kollinear bo‘ladi?
141. А(2; 7; –3) va В(–6; –2; 1) nuqtalar berilgan. BA vektorni koordinatalar vektorlari (ortlari) bo‘yicha yoying.
1. Oxy tekisligiga nisbatan (1; 2; 3) nuqtaga simmetrik bo‘lgan nuqtani toping.
![]()
2. Agar a(6; 3; 2) va b(–3; 1; 5) bo‘lsa, c= a+2b vektorning uzunligini toping.
3. A(2; –1; 0) va B(–2; 3; 2) nuqtalar berilgan. Koordinata boshidan AB kesma o‘rtasigacha bo‘lgan masofani toping
4. A(1; –2; 2), B(1; 4; 0), C(–4; 1; 1) va D(–5; –5; 3) nuqtalar berilgan.
![]()
AC va BD vektorlar orasidagi burchakni toping.
5. (Yaxshi o‘zlashtiradigan o‘quvchilar uchun qo‘shimcha masala). Uchlari A(4; 5; 1), B(2; 3; 0) va C(2; 1; –1) nuqtalarda bo‘lgan uchburchakning BD medianasi uzunligini toping
 I BOB. PRIZMA VA
SILINDR
I BOB. PRIZMA VA
SILINDR5. KO‘PYOQLI BURCHAKLAR VA KO‘PYOQLAR
Ikkiyoqli burchak bilan 10- sinfda tanishgansiz.
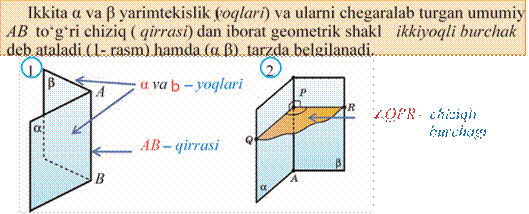
Ikkiyoqli burchak qirrasining ixtiyoriy P nuqtasi dan uning yoqlarida yotuvchi va bu qirraga perpendikular bo‘lgan PR va PQ nurlarni chiqaramiz.
∠QPR – ikkiyoqli burchakning chiziqli burchagi deb ataladi (2- rasm).
Ikkiyoqli burchaklar yassi burchaklar kabi chiziqli burchagining kattaligiga qarab o‘tkir, o‘tmas, to‘g‘ri va yoyiq bo‘ladi (3- rasm). Yassi burchaklar kabi ikkita ikkiyoqli burchaklar qo‘shni va vertikal bo‘lishi mumkin (4- rasm).
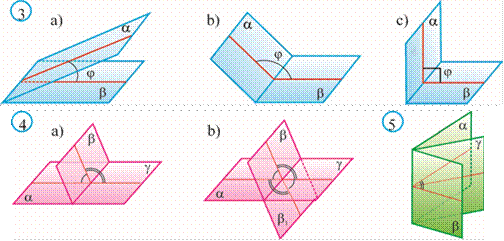
Ikkiyoqli burchakni teng ikkiga bo‘luvchi yarimtekislik uning bissektori deb ataladi (5- rasm).
![]() 1- masala. Chiziqli burchagi 60o ga teng bo‘lgan ikkiyoqli
burchakning yoqlarida yotgan A va B nuqtalardan (6- rasm) uning
qirrasiga AA1 va BB1 perpendikularlar tushirilgan. Agar AA1 = 12, BB1 = 10 va A1B1 = 13 bo‘lsa, AB kesma uzunligini toping.
1- masala. Chiziqli burchagi 60o ga teng bo‘lgan ikkiyoqli
burchakning yoqlarida yotgan A va B nuqtalardan (6- rasm) uning
qirrasiga AA1 va BB1 perpendikularlar tushirilgan. Agar AA1 = 12, BB1 = 10 va A1B1 = 13 bo‘lsa, AB kesma uzunligini toping.
Yechish. BB1||CA1 va A1B1||CB to‘g‘ri chiziqlarni o‘tkazamiz. Hosil bo‘lgan A1B1BC to‘rtburchak parallelogramm bo‘ladi. A1B1 to‘g‘ri chiziq A1AC uchburchak tekisligiga perpendikular bo‘ladi, chunki u bu tekislikda yotgan ikkita A1A va A1C to‘g‘ri chiziqlarga perpendikular. Unda BC to‘g‘ri chiziq ham bu tekislikka perpendikular bo‘ladi.
Demak, ABC uchburchak to‘g‘ri burchakli uchburchak ekan.
Kosinuslar teoremasiga ko‘ra:
![]() AC2 = AA
AC2 = AA![]() a = 122 + 102 – 2·12·10∙cos60°=124.
Pifagor teoremasiga ko‘ra: AB AC2 BC2 124169 293.
a = 122 + 102 – 2·12·10∙cos60°=124.
Pifagor teoremasiga ko‘ra: AB AC2 BC2 124169 293.
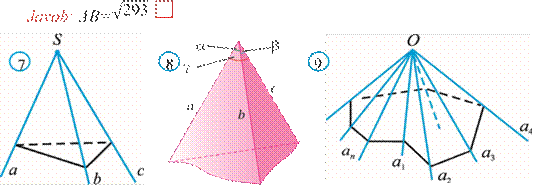
|
Fazoda bir nuqtadan chiquvchi a, b va c nurlar uchta yassi (ab), (bc) va (ac) burchaklar tashkil qiladi (7- rasm). Bu yassi burchaklardan tashkil topgan (abc) shaklga uchyoqli burchak deyiladi. Yassi burchaklarga uchyoqli burchakning yoqlari, ularning tomonlariga uchyoqli burchakning qirralari, umumiy uchiga esa uchyoqli burchakning uchi deyiladi. |
|
Uchyoqli burchakning yoqlaridan tashkil qilgan ikkiyoqli burchaklar uchyoqli burchakning ikkiyoqli burchaklari deb ataladi. |
|
Uchta yassi (ab), (bc) va (ac) burchaklar uchyoqli burchakning tekis burchaklari deb ham yuritiladi. |
Uchyoqli burchakning tekis burchaklarini, mos ravishda, a, b, g deb belgilasak (8- rasm), ular uchun uchburchak tengsizligi o‘rinli bo‘ladi, ya’ni ularning ixtiyoriysi qolgan ikkitasining yig‘indisidan kichik bo‘ladi: a+b<g, a+g<b, b+g<a va tekis burchaklarining yig‘indisi 360o dan kichik bo‘ladi: a+b+g<360°.
Ko‘pyoqli burchak tushunchasi ham shunga o‘xshash kiritiladi (9- rasm).
E’tibor bergan bo‘lsangiz, shu choqqacha fazoviy shakl sifatida qator jismlarning, xususan ko‘pyoqlarning xossalarini o‘rganib keldik. Bu fazoviy shakllarning jism deb atalishiga sabab, ularni fazoning biror moddiy jism egallagan va sirt bilan chegaralangan bo‘lagi sifatida tasavvur etish mumkinligidir. Quyida ko‘pyoqlarga tegishli ba’zi tushunchalarni eslatib o‘tamiz.
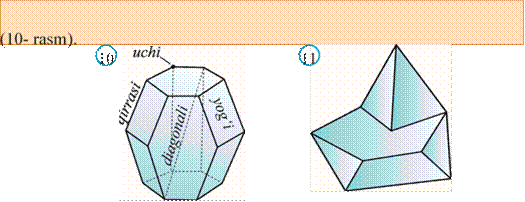 Ko‘pyoq deb yassi ko‘pburchaklar bilan chegaralangan jismga aytiladi
Ko‘pyoq deb yassi ko‘pburchaklar bilan chegaralangan jismga aytiladi
Ko‘pyoq ixtiyoriy yog‘i yotgan tekislikning bir tomonida yotsa, bunday ko‘pyoq qavariq ko‘pyoq deyiladi. 10- rasmda qavariq, 11- rasmda esa qavariq bo‘lmagan ko‘pyoqlar tasvirlangan.
Ixtiyoriy qavariq ko‘pyoqning yoqlari sonini Y, uchlari sonini U va qirralari sonini Q bilan belgilaylik. Bizga ma’lum ko‘pyoqlar uchun quyidagi jadvalni to‘ldiraylik:
|
|
Ko‘pyoq nomi |
Y |
U |
Q |
|
|
Uchburchakli piramida |
4 |
4 |
6 |
||
|
To‘rtburchakli piramida |
5 |
5 |
8 |
||
|
Uchburchakli prizma |
5 |
6 |
9 |
||
|
|
To‘rtburchakli prizma |
6 |
8 |
12 |
|
|
n- burchakli piramida |
n+1 |
n+1 |
2n |
||
|
n- burchakli prizma |
n+2 |
2n |
3n |
Jadvaldan har bir ko‘pyoq uchun Y + U – Q = 2 bo‘lishini payqash mumkin. Ma’lum bo‘lishicha, bu munosabat barcha qavariq ko‘pyoqlar uchun to‘g‘ri bo‘lar ekan. Buni ilk bor 1752- yilga shvetsariyalik matematik Leonard Eyler aniqlagan.
Eyler teoremasi. Ixtiyoriy qavariq ko‘pyoq uchun: Y + U – Q = 2 munosabat o‘rinli bo‘ladi, bu yerda Y– ko‘pyoqning yoqlari, U – uchlari, Q– esa qirralari soni.
Bu teoremaning isbotiga to‘xtalmaymiz. Undan quyidagi natijalar kelib chiqadi. Ularni Eyler teoremasidan foydalanib mustaqil isbotlang.
|
1- natija. Ko‘pyoq tekis burchaklarining soni uning qirralari sonidan ikki marta ko‘p. |
|
2- natija. Ko‘pyoq tekis burchaklari soni har doim juft bo‘ladi. |
|
3- natija. Agar ko‘pburchakning har bir uchida bir xil k sondagi qirralar tutashsa, U . k = 2Q munosabat o‘rinli bo‘ladi. |
|
4- natija. Agar ko‘pyoqning barcha yoqlari bir xil n-burchaklardan tashkil topgan bo‘lsa, Y = 2Q munosabat o‘rinli bo‘ladi. |
|
5- natija. Ko‘pyoqning tekis burchaklari yig‘indisi 360°(Y– Q) ga teng. |
|
Yoqlari bir-biriga teng muntazam ko‘pburchaklardan iborat va har bir uchidan bir xil sondagi qirralar chiqadigan qavariq ko‘pyoqli muntazam ko‘pyoqli deb ataladi. |
Ma’lum bo‘lishicha muntazam ko‘pyoqlilar besh xil bo‘lar ekan (buni mustaqil tekshirib ko‘ring). Bular quyidagilar:
|
Shakli |
|
|
|
|
|
|
Nomi va uning talqini |
muntazam tetraedr (to‘rtyoqli) |
Kub, geksaedr (oltiyoqli) |
Oktaedr (sakkizyoqli) |
Dode- kaedr (o‘n ikkiyoqli) |
Ikosaedr (yigirmayoqli) |
|
Yoqlari |
muntazam uchburchak |
munta- zam to‘rtburchak |
muntazam uchburchak |
munta- zam beshbur chak |
munta- zam uchburchak |
|
Yoqlari soni |
4 |
6 |
8 |
12 |
20 |
|
Qirralari soni |
6 |
12 |
12 |
30 |
30 |
|
Uchlari soni |
4 |
8 |
6 |
20 |
12 |
|
Har bir uchdan chiquvchi qirralar soni |
3 |
3 |
4 |
3 |
5 |
![]() Barcha muntazam ko‘pyoqlar
Qadimgi Yunonistonda ma’lum edi. Yevklidning mashhur “Negizlar”ining XIII
kitobi muntazam ko‘pyoqlarga bag‘ishlangan. Bu ko‘pyoqlarni ko‘pincha Platon
jismlari deb ataladi. Qad imgi Yunonistonning buyuk olimi Platon (miloddan oldingi
427–347- yillar) bayon qilgan olamning idealistik tasvirida bu jismlardan
to‘rttasi olamning to‘rt unsuriga (elementiga) o‘xshatilgan:
Barcha muntazam ko‘pyoqlar
Qadimgi Yunonistonda ma’lum edi. Yevklidning mashhur “Negizlar”ining XIII
kitobi muntazam ko‘pyoqlarga bag‘ishlangan. Bu ko‘pyoqlarni ko‘pincha Platon
jismlari deb ataladi. Qad imgi Yunonistonning buyuk olimi Platon (miloddan oldingi
427–347- yillar) bayon qilgan olamning idealistik tasvirida bu jismlardan
to‘rttasi olamning to‘rt unsuriga (elementiga) o‘xshatilgan:
tetraedr – olov, geksaedr – Yer, ikosaedr – suv, oktaedr – havo, beshinchi ko‘pyoq – dodekaedr esa butun olam tuzilishining belgisi (“beshinchi mohiyat”) deb atashgan.
XVIII asrda ko‘pyoqlar nazariyasiga Leonard Eyler (1707–1783) salmoq li hissa qo‘shdi. 1758- yilda e’lon qilingan qavariq ko‘pyoqlarning uchlari, qirralari va yoqlari soni orasidagi muosabat haqidagi Eyler teoremasi va uning isboti rang-barang ko‘pyoqlar dunyosiga tartib o‘rnatdi va uning go‘zal geometrik zojibasini algebraik nuqtayi nazaridan bayon etdi.
142. Ikki tekislik orasidagi burchak 47°. Bu tekisliklar kesishishidan hosil bo‘lgan ikkiyoqli burchaklarning gradus o‘lchovini toping.
143. Ikkiyoqli burchakning gradus o‘lchovi 52° ga teng. Bu burchakka qo‘shni bo‘lgan ikkiyoqli burchakning gradus o‘lchovi nimaga teng bo‘ladi?
144. Tekis burchagi 100° bo‘lgan ikkiyoqli burchakning yoqlariga perpendikular bo‘lgan to‘g‘ri chiziqlar orasidagi burchakni toping.
145. Qo‘shni ikkiyoqli burchaklarning bissektorlari orasidagi ikkiyoqli burchakning gradus o‘lchovi nimaga teng?
146. A nuqta gradus o‘lchovi 60° bo‘lgan ikkiyoqli burchakning bissektorida yotibdi. Agar bu nuqta ikkiyoqli burchak qirrasidan 10 cm masofada yotgan bo‘lsa, unda ikkiyoqli burchakning yoqlarigacha bo‘lgan masofalarni toping.
147. A nuqta gradus o‘lchovi 30° bo‘lgan ikkiyoqli burchakning bitta yog‘iga tegishli bo‘lib, ikkinchi yog‘idan 6 cm masofada yotibdi. Bu nuqtadan ikkiyoqli burchakning qirrasigacha bo‘lgan masofani toping.
148*. A nuqta to‘g‘ri ikkiyoqli burchakning yoqlaridan 3 dm va 4 dm masofada yotibdi. Bu nuqtadan ikkiyoqli burchakning qirrasigacha bo‘lgan masofani toping.
149*. Muntazam tetraedrning barcha ikkiyoqli burchaklari teng ekanligini isbotlang va ularning gradus o‘lchovini toping.
150. Tekis burchaklari: a) 30°; 60°; 20°; b) 45°; 80°; 130°; c) 30°; 60°; 20°;
d) 20°; 60°; 70°; e) 76°; 34°; 110° bo‘lgan uch yoqli burchak mavjudmi?
151*.Qavariq ko‘pyoqli burchakning barcha tekis burchaklari yig‘indisi 360° dan kichik ekanligini isbotlang.
152. To‘g‘ri burchakli parallelepipedda AB=5, AD=4 va AA1=3 bo‘lsa, ABD1 burchakni toping (12- rasm).
153. To‘g‘ri burchakli parallelepipedda AB=4, AD=3 va AA1=5 bo‘lsa, DBD1 burchakni toping (13- rasm).
154. 14- rasmda berilgan kubdagi DBH burchakni toping.
155*. n ta uchi bor qavariq ko‘pyoqning barcha tekis burchaklari yig‘indisi 360°(n – 2) ga teng ekanligini isbotlang.
156*.Ko‘pyoq tekis burchaklarining soni uning qirralari sonidan ikki marta ko‘p bo‘lishini isbotlang.
157*.Ko‘pyoq tekis burchaklari soni har doim juft bo‘lishini isbotlang.
158*.Ko‘pyoqning tekis burchaklari yig‘indisi 360° (Y – Q) ga teng bo‘lishini isbotlang..
159. 15- rasmlardagi kublarda ajratib ko‘rsatilgan burchaklar kattaligini aniqlang.
160*.16- rasmlardagi kubning sirtidagi pashshaga: a) A uchdan B uchga;
b) kub yog‘ining markazidan qarama-qarshi yog‘ining markaziga olib boradigan eng qisqa yo‘lni ko‘rsating (ko‘rsatma: kubning yoyilmasidan foydalaning).
161. 17- rasmda tasvirlangan fazoviy shakl muntazam ko‘pyoqli bo‘ladimi?
Uning sirti nechta kvadratdan iborat? Uning nechta uchi va qirrasi bor?
162. 18- rasmda tasvirlangan yoyilmalarning qaysi biri oktaedrga tegishli?163. 19- rasmda tasvirlangan, kubga ichki chizilgan ko‘pyoqning: a) muntazam tetraedr; b) oktaedr ekanligini asoslang.
164. 20- rasmda tasvirlangan ko‘pyoqlarning uchlari, qirralari va yoqlari sonini aniqlab, ularni Eyler tenglamasiga qo‘yib tekshiring.
165. Qavariq ko‘pyoqning har bir uchidan uchtadan qirra chiqadi. Agar bu ko‘pyoqning qirralar soni: a) 12; b) 15 ga teng bo‘lsa, uning nechta uchi va yog‘i bor?
166*.13 ta yog‘i va har bir yog‘ida 13 tadan qirrasi bo‘lgan ko‘pyoq mavjudmi?
167. Qavariq ko‘pyoqning har bir uchidan to‘rttadan qirra chiqadi. Agar bu ko‘pyoqning qirralar soni 12 ga teng bo‘lsa, uning nechta uchi va yog‘i bor?
168. a) Muntazam tetraedr; b) kub; c) oktaedr; d) dodekaedr; e) ikosaedrning uchlari, qirralari va yoqlari sonini toping va bu ko‘pyoqlar uchun Eyler tenglamasining o‘rinli bo‘lishini tekshiring.
169. Uchlari soni 8 ta, qirralari soni esa 12 ta bo‘lgan muntazam ko‘pyoqning yoqlari sonini toping va uning nomini aniqlang.
170. Uchlari soni 6 ta, qirralari soni esa 12 ta bo‘lgan muntazam ko‘pyoqning yoqlari sonini toping va uning nomini aniqlang.
171. ![]() Uchlari soni 10 ta, yoqlari soni esa 7 ta bo‘lgan ko‘pyoqning
qirralari sonini toping.
Uchlari soni 10 ta, yoqlari soni esa 7 ta bo‘lgan ko‘pyoqning
qirralari sonini toping.
172. Uchlari soni 14 ta, qirralari soni esa 21 ta bo‘lgan ko‘pyoqning yoqlari sonini toping.
173. 21- rasmdagi ko‘pyoqning 62 ta yog‘i va 120 ta uchi bor bo‘lsa, uning qirralari sonini toping.
Prizmalar bilan quyi sinflardan tanishsiz. Shunday bo‘lsada, ularga oid ba’zi tushuncha va xossalarni eslatib o‘tamiz.
Prizma deb ikki yog‘i (asosi) teng n burchakdan, qolgan n ta yoqlari esa parallelogrammlardan iborat ko‘pyoqqa aytiladi (22- rasm).
Prizma yon yoqlarining asosiga perpendikular yoki perpendikular emasligiga qarab to‘g‘ri yoki og‘ma prizmalarga ajratiladi. 23.a- rasmda to‘g‘ri oltiburchakli prizma, 23.b- rasmda esa og‘ma uchburchakli prizma tasvirlangan. Ravshanki, to‘g‘ri prizmaning yon yoqlari to‘g‘ri to‘rtburchaklardan iborat bo‘ladi.
|
Asosi muntazam ko‘pburchakdan iborat to‘g‘ri prizma muntazam prizma deb ataladi (24- rasm). Muntazam prizmaning yon yoqlari bir-biriga teng to‘g‘ri to‘rtburchaklardan iborat bo‘ladi. |
|
Prizma asosining biror nuqtasidan ikkinchi asosiga tushirilgan perpendikular prizmaning balandligi deb ataladi (23.b- rasm). |
|
Prizmaning diagonal kesimi deb, prizma asoslarining mos diagonallari orqali o‘tkazilgan kesimga aytiladi (24.a- rasm). Prizma diagonal kesimlarin ing soni prizma bitta asosining diagonallari soniga teng. |
|
Prizmaning perpendikular kesimi deb, uning barcha yon qirralariga perpendikular kesimga aytiladi (25- rasm). |
n n( − 3)
Qavariq n-burchakning ta diagonali borligini hisobga olsak,
2 n n( − 3)
n-burchakli prizma diagonal kesimlari soni ham ta bo‘ladi. 2
Har bir diagonal kesimda prizmaning ikkita diagonalini o‘tkazish mumkin. Demak, n-burchakli prizmaning jami n(n–3) ta diagonali bor.
1- masala. Uchburchakli og‘ma prizma yon qirralari orasidagi masofalar, mos ravishda, 7 cm, 15 cm va 20 cm. Prizmaning eng katta yuzli yon yog‘idan uning qarshisidagi yon qirrasigacha bo‘lgan masofani toping.
Yechish. Ma’lumki, parallel to‘g‘ri chiziqlar orasidagi masofa bu to‘g‘ri chiziqlar birining biror nuqtasidan ikkinchisiga o‘tkazilgan perpendikularning uzunligiga teng. Unda berilgan prizmaning ABC perpendikular kesimi tomonlarining uzunligi shu masofalarga teng bo‘ladi (26- rasm). Prizmaning eng katta yuzli yog‘ida eng katta AC=20 cm tomon yotadi. B2B1 qirradan A2A1C1C2 tekislikkacha bo‘lgan masofa ABC uchburchakning BD balandligiga teng bo‘ladi. Unda Geron formulasiga ko‘ra:
![]()
![]() SABC = p (p
−a)(p
−b)(p
−c), p a bc , p a bc
SABC = p (p
−a)(p
−b)(p
−c), p a bc , p a bc ![]() 21, 2
21, 2
2 2
![]() SABC 21(21 7)(2115)(21 20) 21 14 6 1 42 .
SABC 21(21 7)(2115)(21 20) 21 14 6 1 42 .
Ikkinchi tomondan, SABC AC BD .
Bundan, 42 AC BD yoki BD =2 4,2 cm.
2 Javob: 4,2 cm.
Asoslari parallelogrammdan iborat prizma parallelepiped deb ataladi (27- rasm). Parallelepipedlar ham prizma kabi to‘g‘ri (27.a- rasm) va og‘ma (27.b- rasm) bo‘lishi mumkin.
![]() 27 a)
27 a)  b)
b) 
Parallelepipedning umumiy uchga ega bo‘lmagan yoqlari qaramaqarshi yoqlari deb ataladi.
Parallelepipedning
− 12 ta qirralari bo‘lib, ularning har to‘rttasi teng kesmalardan iborat (28.a- rasm),
− 6 ta yoqlari bo‘lib, uning qarama-qarshi yoqlari o‘zaro parallel va teng bo‘ladi (28.b- rasm),
− 4 ta diagonali bo‘lib, ular bitta nuqtada keshishadi va kesishish nuqtasida teng ikkiga bo‘linadi (28.c- rasm),
− diagonallari keshishish nuqtasi uning simmetiya markazi bo‘ladi (28.c- rasm).
To‘g‘ri parallelepipedning simmetriya o‘qi (28.d- rasm) va simmetriya tekisligi bor (28.e -rasm).
Asoslari to‘g‘ri to‘rtburchakdan iborat to‘g‘ri parallelepiped to‘g‘ri burchakli parallelepiped deb ataladi (29- rasm).
Ravshanki, to‘g‘ri burchakli parallelepipedning barcha yoqlari to‘g‘ri to‘rtburchaklardan iborat bo‘ladi.
To‘g‘ri burchakli parallelepipedning uchta simmetriya o‘qi (30- rasm) va uchta simmetriya tekisligi bor (31- rasm).
To‘g‘ri burchakli parallelepipedning bitta uchidan chiquvchi uchta qirrasi uzunliklariga uning o‘lchamlari deb aytiladi.
|
Xossa: To‘g‘ri burchakli parallelepiped d diagonalining kvadrati uning o‘lchamlari: a, b va c ning kvadratlari yig‘indisiga teng (32- rasm): d2 = a2 + b2 + c2. |
|
O‘lchamlari teng bo‘lgan to‘g‘ri burchakli parallelepiped kub deb ataladi. |
Ravshanki, kubning barcha yoqlari teng kvadratlardan iborat bo‘ladi. Kub bitta simmetriya markaziga, 9 ta simmetriya o‘qiga va 9 ta simmetriya tekisligiga ega.
Yuqorida prizmalarning qator xossalarini sanab o‘tdik. Ularning ba’zila rini 10- sinfda isbotlagan edik. Qolgan xossalarni isboti nisbatan sodda bo‘lganligi uchun ularni mustaqil isbotlash uchun qoldirdik.
33- rasmda ABCDEA1B1C1D1E1 prizmaning HH1 va DD1 balandliklari tasvirlangan. Ravshanki, muntazam prizmaning balandligi uning yon qirrasiga teng bo‘ladi.
|
Prizma yon sirti (aniqrog‘i, yon sirtining yuzi) uning yon yoqlari yuzi yig‘indisiga teng, to‘la sirti esa yon sirti va ikkita asosining yuzi yig‘indisiga teng Sto‘la = Syon + 2Sasos . |
|
Teorema. To‘g‘ri prizmaning yon sirti asosining perimetri bilan baland ligining ko‘paytmasiga teng: Syon = Pasos ∙ h. |
.
Isbot. Berilgan prizmaning balandligi h, asosining perimetri
P = AB + BC + … + KA bo‘lsin (34- rasm). Ravshanki, to‘g‘ri prizmaning
har bir yog‘i to‘g‘ri to‘rtburchakdan iborat. Bu to‘g‘ri to‘rtburchaklarning asosi prizmaning mos tomonlariga, balandligi esa prizma balandligiga teng.
Demak, Syon=AB ∙ h+ BC ∙ h+...+ KA ∙ h=(AB+ BC + …
KA)∙ h = P∙ h. ![]()
Teorema. Ihtiyority prizmaning yon sirti uning perpendikular kesimi perimetri bilan yon qirrasi uzunligining ko‘paytmasiga teng:
Syon = P ∙ l.
![]() Isbot. Perpendikular
kesimning perimetri P ga teng bo‘lsin (35- rasm). Kesim prizmani ikki
bo‘lakka ajratadi (36.a- rasm). Bu bo‘laklarning birini olib, prizma asoslari
ustma-ust tushadigan qilib parallel ko‘chiramiz. Natijada yangi to‘g‘ri prizma
hosil bo‘ladi (36.b- rasm). Ravshanki, bu prizmaning yon sirti berilgan prizma
yon sirtiga teng. Uning asosi berilgan perpendikular kesimdan iborat bo‘lib,
yon qirrasi l ga teng bo‘ladi.
Isbot. Perpendikular
kesimning perimetri P ga teng bo‘lsin (35- rasm). Kesim prizmani ikki
bo‘lakka ajratadi (36.a- rasm). Bu bo‘laklarning birini olib, prizma asoslari
ustma-ust tushadigan qilib parallel ko‘chiramiz. Natijada yangi to‘g‘ri prizma
hosil bo‘ladi (36.b- rasm). Ravshanki, bu prizmaning yon sirti berilgan prizma
yon sirtiga teng. Uning asosi berilgan perpendikular kesimdan iborat bo‘lib,
yon qirrasi l ga teng bo‘ladi.
174. Tetraedr bitta yog‘ining yuzi 6 cm2 bo‘lsa, uning to‘la sirtini toping.
175. Oktaedr bitta yog‘ining yuzi 5,5 cm2 bo‘lsa, uning to‘la sirtini toping.
176. Dodekaedr bitta yog‘ining yuzi 6,4 cm2 bo‘lsa, uning to‘la sirtini toping.
177. Kub to‘la sirtining yuzi 105,84 cm2 bo‘lsa, uning har bir yog‘i yuzini va qirrasining uzunligini toping.
178. ![]() Oktaedr
to‘la sirtining yuzi 32 3 cm2 bo‘lsa, uning har bir yog‘i yuzini va qirrasining uzunligini
toping.
Oktaedr
to‘la sirtining yuzi 32 3 cm2 bo‘lsa, uning har bir yog‘i yuzini va qirrasining uzunligini
toping.
179. To‘g‘riburchakli parallelepiped asosining tomonlari 7:24 nisb atda, diagonal kesimining yuzi 50 dm2 ga teng.Yon sirtining yuzini toping.
180*.To‘g‘ri parallelepipedning yon qirrasi 1 m ga, asoslarining tomonlari 23 m va 11 m ga teng. Asos diagonallarining nisbati 2:3 kabi. Diagonal kesimlarining yuzini toping.
181. To‘g‘ri parallelepiped asosining tomonlari 3 cm va 5 cm, asosining diagonallaridan biri 4 cm ga teng. Parallelepiped kichik diagonallaridan biri asos tekisligi bilan 60° li burchak tashkil etadi. Uning diagonallari uzunligini toping.
182. To‘g‘ri parallelepipedning yon qirrasi 5 m, asosining tomonlari 6 m va 8 m, asosining diagonallaridan biri 12 m ga teng. Parallelepipedninng diagonallarini toping.
183*.Uchburchakli muntazam prizmaning qirrasi 3 ga teng. Asosining tomoni va o‘qining o‘rtasi orqali tekislik o‘tkazilgan. Kesimning yuzini toping.
184. Uchburchakli to‘g‘ri prizmaning balandligi 50 cm, asosining tomonlari 40 cm, 13 cm va 37 cm. Prizmaning to‘la sirtini toping.

185*.37- rasmda tasvirlangan birlik kubdan asosining tomoni 0,5 ga yon qirrasi 1 ga teng bo‘lgan muntazam to‘rtburchakli prizma o‘yib olindi. Kubning qolgan bo‘lagi to‘la sirtining yuzini hisoblang.
186. Agar kubning qirrasi 1 birlik orttirilsa, uning to‘la sirti 54 birlikka ortadi. Kubning qirrasini toping (38- rasm).
187. ABCC1B1A1 og‘ma prizmaning asosi ABC tengyonli uchburchak bo‘lib, unda AB=AC=10 cm va BC=12 cm. A1 uchi A, B va C uchlardan teng uzoqlikda yotadi hamda AA1 kesma 13 cm ga teng. Prizmaning to‘la sirtini toping.
188. Muntazam to‘rtburchakli prizmaning yon sirti 160 ga, to‘la sirti 210 ga teng. Prizma asosining diagonalini toping.
189. Uchburchakli og‘ma prizmaning yon qirralari yotgan parallel to‘g‘ri chiziqlar orasidagi masofa 2 cm , 3 cm va 4 cm, yon qirralari esa 5 cm ga teng. Prizmaning yon sirtini toping.
190. Kubning qirralari uzunliklari yig‘indisi 96 ga teng. Uning yon sirtini toping.
191. 39- rasmlarda tasvirlangan ko‘pyoqlarning to‘la sirtini hisoblang(hamma ikkiyoqli burchaklar to‘g‘ri burchak).
192. 40- rasmlarda tasvirlangan ko‘pyoqlarning to‘la sirtini hisoblang(hamma ikkiyoqli burchaklar to‘g‘ri burchak).
193. Oltiburchakli muntazam prizmaning yon qirrasi 8 cm, asosining tomoni esa 3 cm. Prizmaning barcha qirralari uzunliklarining yig‘indisini toping.
194. To‘rtburchakli muntazam prizma asosining tomoni 6 cm, prizmaning balandligi esa 5 cm. Uning diagonal kesimi yuzini toping.
195. Uchburchakli muntazam prizma asosining tomoni 6 cm, yon qirrasi esa 12 cm. Prizma yon sirtining yuzini toping.
196. 41- rasmlarda tasvirlangan ko‘pyoqlarning to‘la sirtini hisoblang(hamma ikkiyoqli burchaklar to‘g‘ri burchak).
197. 42- rasmlarda tasvirlangan ko‘pyoqlarning to‘la sirtini hisoblang (hamma ikkiyoqli burchaklar to‘g‘ri burchak).
198*.43- rasmdadagi uy asosining o‘lchamlari 6 m va 8 m. Uyning tomi asosiga 45° li burchak ostida og‘gan. Tom sirti yuzini toping.
199. Parallelepipedning bitta uchidan chiquvchi qirralari, mos ravishda, 6 cm, 8 cm va 12 cm. Parallelepiped barcha qirralari uzunliklarining yig‘indisini toping.
200. Parallelepipedning bitta umumiy uchga ega yoqlarining yuzlari 6 cm2, 12 cm2 va 16 cm2. Parallelepiped to‘la sirtining yuzini toping.
201*.Qirrasi 3 cm ga teng bo‘lgan kubning har bir yog‘idan ko‘ndalang kesimi - asosi 1 cm ga teng kvadrat shaklidagi teshiklar o‘yilgan (44- rasm). Kubning qolgan qismi to‘la sirtining yuzini toping.
202*.Futbol to‘pining sirti qirralari 5 cm ga teng bo‘lgan 12 ta muntazam beshburchak va 20 ta muntazam oltiburchakdan iborat (45- rasm). Futbol to‘pining to‘la sirtini toping. To‘p kvadrat santimetri 60 so‘m turadigan charmdan ishlangan va uning 10 foizi chok va chiqitga chiqishi ma’lum bo‘lsa, to‘pga sarflangan charm narxini toping.
7. PRIZMANING HAJMI
Fazoda geometrik jismga xos bo‘lgan xususiyatlardan biri bu hajm tushunchasidir. Har qanday predmet (jism) fazoning qandaydir qismini egallaydi. Masalan, g‘isht gugurt qutisiga qaraganda kattaroq joyni egallaydi. Bu qismlarni o‘zaro taqqoslash uchun hajm tushunchasi kiritiladi.
Hajm – fazoviy jismning quyidagi xossalarga ega bo‘lgan miqdoriy (sonli) ko‘rsatkichidir:
1. Har qanday jism musbat sonlarda ifodalanuvchi muayyan hajmga ega.
2. Teng jismlar hajmi ham teng.
3. Agar jism bir necha bo‘lakka bo‘lingan bo‘lsa, uning hajmi bo‘laklar hajmlari yig‘indisiga teng.
4. Qirrasi bir birlik uzunlikka teng kubning hajmi birga teng.
Hajm – uzunlik va yuz kabi sonli kattaliklardan biridir. Uzunlik o‘lchov birligining tanlanishiga qarab birlik (qirrasi birlik uzunlikka ega) kub ning hajmi 1 cm3, 1 dm3, 1 m3 va hokazo hajm birliklari bilan o‘lchanadi.
Jismlar hajmini turli usullar bilan o‘lchashadi yoki hisoblashadi. Masalan, kichikroq detalning hajmini bo‘linmalarga (shkalaga) ega bo‘lgan idish (menzurka) yordamida o‘lchash mumkin (46- rasm). Chelak hajmini esa unga birlik hajmga ega bo‘lgan idish yordamida suv quyib, to‘ldirish bilan o‘lchash mumkin (47- rasm). Lekin hamma jismlarning ham hajmni bunday usullar bilan o‘lchab bo‘lmaydi. Bunday hollarda hajm turli usullar bilan hisoblanadi. Quyida shu usullar xususida to‘xtalamiz va ularning ba’zilarini isbotsiz keltiramiz.
|
Teorema. To‘g‘ri burchakli parallelepipedning hajmi uning uchta o‘lchamlari ko‘paytmasiga teng (48- rasm): V = a ∙ b ∙ c. |
|
Natija. To‘g‘ri burchakli parallelepipedning hajmi asosining yuzi bilan balandligining ko‘paytmasiga teng (49- rasm): V = S ∙ h. |
|
Teorema. Ixtiyoriy parallelepipedning hajmi asosining yuzi bilan balandligining ko‘paytmasiga teng (50- rasm): V = S ∙ h. |
Mazkur xossa yuqoridagi natijadan kelib chiqadi. Quyidagi 50- rasmlarda berilgan parallelepiped qanday qilib to‘g‘ri burchakli para llelepipedga to‘ldirilishi tasvirlangan. Bundan foydalanib xossani mustaqil asoslang.
Teorema. To‘g‘ri prizmaning hajmi asosining yuzi bilan balandligining ko‘paytmasiga teng (51- rasm): V = S ∙ h.
Isbot. 1- hol. Asosi to‘g‘ri burchakli uchburchakdan iborat to‘g‘ri prizma berilgan bo‘lsin (51.a- rasm). Bu prizmani unga teng bo‘lgan prizma bilan to‘g‘ri burchakli paralelepipedgacha to‘ldirish mumkin (51.b- rasm).
Berilgan prizmaning hajmi, asosining yuzi va balandligi, mos ravishda, V, S va h bo‘lsa, hosil bo‘lgan to‘g‘ri burchakli parallelepipedning hajmi, asosining yuzi va balandligi, mos ravishda, 2V, 2S va h bo‘ladi.
Demak, 2V=2S · h yoki V=S · h bo‘ladi.
2- hol. Ixtiyoriy to‘g‘ri n-burchakli prizma berilgan bo‘lib, uning asosi yuzi S, balandligi esa h ga teng bo‘lsin. Prizmaning asosi – n-burchakni uning diagonallari bilan uchburchaklarga, uchburchaklarning har birini esa to‘g‘ri burchakli uchburchaklarga bo‘lish mumkin (52- rasm). Natijada, berilgan prizmani chekli sondagi asosi to‘g‘ri burchakli uchburchaklardan iborat to‘g‘ri prizmalarga ajratish mumkinligini aniqlaymiz. Bu prizmalarning balandligi h ga teng bo‘lib, ularning asoslari yig‘indisi berilgan prizma yuziga teng bo‘ladi: S = S1+ S2+...+Sk.
Berilgan prizmaning hajmi uni tashkil qiluvchi uchburchakli prizmalar hajmlari yig‘indisidan iborat bo‘ladi:
V = S1h + S2h +...+Sk h=(S1+S2+...+Sk) h = S ∙ h,
yoki V = S ∙ h. ![]()
|
Teorema. Ixtiyoriy prizmaning hajmi asosining balandligining ko‘paytmasiga teng: V = S ∙ h. |
yuzi |
bilan |
Bu teoremani 5.3- rasmdan foydalanib, oldin uchburchakli prizma uchun (5.3.a- rasm), so‘ng ixtiyoriy prizma uchun (5.3.b- rasm) mustaqil isbotlang.
1- masala. To‘g‘ri parallelepiped asosining tomonlari a va b ga teng bo‘lib, ular o‘zaro 30° li burchak tashkil qiladi. Agar parallelepipedning yon sirti S ga teng bo‘lsa, uning hajmini toping.
![]() Yechish: Parallelepiped
balandligini h bilan belgilaymiz (54- rasm). Unda shartga ko‘ra:
Yechish: Parallelepiped
balandligini h bilan belgilaymiz (54- rasm). Unda shartga ko‘ra:
S = (2a+2b)
h yoki h ![]() S . 2(a b ) Sasos absin30 ab2 .
S . 2(a b ) Sasos absin30 ab2 .
204. 56- rasmda berilgan yoyilmaga ko‘ra yasalgan idishning hajmini toping.
205*. 57- rasmga ko‘ra masala tuzing va uni yeching.
206. 58- rasmda keltirilgan jism 88 ta birlik kubchadan yasalgan. Jismning to‘la sirtini toping.
207. To‘g‘ri burchakli parallelepiped yog‘ining yuzi 12 ga va unga perpendikular qirra uzunligi 12 ga teng. Parallelepipedning hajmini toping.
208. 59- rasmda tasvirlangan fazoviy shakllardan qaysi birining hajmi katta, ya’ni ko‘proq kubchalardan tashkil topgan?
209. To‘g‘ri burchakli parallelepiped hajmi 24 ga teng va qirralaridan birining uzunligi 3 ga teng. Parallelepipedning bu qirraga perpendikular yog‘ining yuzini toping.
210. To‘g‘ri burchakli parallelepiped hajmi 60 ga teng va yoqlaridan biri-ning yuzi 12 ga teng. Parallelepipedning bu yoqqa perpendikular qirraning uzunligini toping.
211. To‘g‘ri burchakli parallelepiped bir uchidan chiquvchi uchta qirralari uzunliklari 4, 6 va 9 ga teng. Unga tengdosh kub qirrasini toping.
212. Kubning to‘la sirti yuzi 18 ga teng bo‘lsa, uning diagonalini toping.
213. Kubning hajmi 8 ga teng bo‘lsa, uning to‘la sirtinining yuzini toping.
214. Agar kubning qirralarini 1 birlik orttirilsa, uning hajmi 19 birlikka ortadi. Kubning qirrasini toping.
215. Kubning to‘la sirtining yuzi 24 ga teng. Uning hajmini toping.
216. ![]() Kubning diagonali 12 ga teng bo‘lsa, uning
hajmini toping.
Kubning diagonali 12 ga teng bo‘lsa, uning
hajmini toping.
217. Kubning hajmi 24 3 ga teng bo‘lsa, uning diagonalini toping.
218. Birinchi kubning hajmi ikkinchisinikidan 8 marta katta. Birinchi kubning to‘la sirtining yuzi ikkinchisinikidan necha marta katta?
219. Qirrasi 30 cm bo‘lgan kub shaklidagi idishga (sisternaga) necha litr suv ketadi?
220. To‘g‘ri burchakli parallelepipedning bitta uchidan chiquvchi qirralari 2 va 6 ga teng. To‘g‘ri burchakli parallelepiped hajmi 48 ga teng. Parallelepipedning shu uchidan chiquvchi uchinchi qirrasini toping.
221. ![]() To‘g‘ri parallelepiped asosining tomonlari uzunligi 2 2 cm va 5 cm, ular orasidagi
burchak 45° ga teng. Agar parallelepipedning kichik diagonali 7 cm ga teng
bo‘lsa, uning hajmini toping.
To‘g‘ri parallelepiped asosining tomonlari uzunligi 2 2 cm va 5 cm, ular orasidagi
burchak 45° ga teng. Agar parallelepipedning kichik diagonali 7 cm ga teng
bo‘lsa, uning hajmini toping.
222*.To‘g‘ri parallelepiped asosining a va b tomonlari 30° li burchak tashkil qiladi. To‘la sirti S ga teng. Uning hajmini toping.
223. To‘g‘ri burchakli parallelepipedning o‘lchamlari 15 m, 50 m va 36 m. Unga tengdosh kubning qirrasini toping.
224. Uchburchakli to‘g‘ri prizma asosining tomonlari 29, 25 va 6 ga, qirrasi esa asosining katta balandligiga teng. Prizmaning hajmini toping.
225. 39- rasmlarda tasvirlangan ko‘pyoqlarning hajmini hisoblang (hamma ikkiyoqli burchaklar to‘g‘ri burchak).
226. 40- rasmlarda tasvirlangan ko‘pyoqlarning hajmini hisoblang (hamma ikkiyoqli burchaklar to‘g‘ri burchak).
227. To‘g‘ri parallelepipedning asosining yuzi 1 m2 bo‘lgan rombdan iborat. Diagonal kesimlarining yuzi, mos ravishda, 3 m2 va 6 m2. Parallelepipedning hajmini toping.
228. 41- rasmlarda tasvirlangan ko‘pyoqlarning hajmini hisoblang (hamma ikkiyoqli burchaklar to‘g‘ri burchak).
229. 42- rasmlarda tasvirlangan ko‘pyoqlarning hajmini hisoblang (hamma ikkiyoqli burchaklar to‘g‘ri burchak).
230. Kengligi 3 m va uzunligi 20 m bo‘lgan yolakka qalinligi 10 cm bo‘lgan asfalt qatlami yotqizildi. Yo‘lak uchun qancha hajmdagi asfalt ishlatildi?
231*. Og‘ma parallelepipedning asosi – tomoni 1 m ga teng bo‘lgan kvadratdan iborat. Yon qirralaridan biri 2 m ga teng va asosining o‘ziga yopishgan har bir tomoni bilan 60° li burchak tashkil etadi. Parallelepipedning hajmini toping.
232*.Parallelepipedning yoqlari – tomoni a ga teng va o‘tkir burchagi 60° bo‘lgan teng romblardan iborat. Parallelepipedning hajmini toping.
233. Parallelepipedning har bir qirrasi 1 cm ga teng. Parallelepipedning bir uchidagi uchala yassi burchagi o‘tkir bo‘lib, har biri 2a ga teng. Parallelepipedning hajmini toping.
234*.Parallelepipedning bir uchidan chiquvchi uchta qirrasining uzunliklari a, b, c ga teng. a va b qirralari o‘zaro perpendikular, c qirra esa ularning har biri bilan a burchak tashkil etadi. Parallelepipedning hajmini toping (60- rasm).
235. a) Uchburchakli; b) to‘rtburchakli; c) oltiburchakli muntazam prizma asosining tomoni a va yon qirrasi b bo‘yicha hajmini toping.
236. To‘g‘ri parallelepiped asosining tomonlari a cm va b cm ga teng bo‘lib, ular o‘zaro a burchak tashkil qiladi. Parallelepipedning kichik diagonali d ga teng bo‘lsa, uning hajmini toping.
237. Uchburchakli og‘ma prizmaning yon qirralari 15 m ga, ular orasidagi masofa esa 26 m, 25 va 17 m ga teng. Prizmaning hajmini toping.
238. To‘rtburchakli muntazam prizmaning diagonali 3,5 cm ga, yon yog‘ining diagonali 2,5 cm ga teng. Prizmaning hajmini toping.
239. Uchburchakli muntazam prizma asosining tomoni a ga, yon sirti asoslari yuzlarining yig‘indisiga teng. Uning hajmini toping.
240. Oltiburchakli muntazam prizmada eng katta diagonal kesimning yuzi4 m2 ga, ikkita qarama-qarshi yon qirralari orasidagi masofa 2 m ga teng. Prizmaning hajmini toping.
241*.Yetti marta kir yuvishdan keyin sovunning o‘lchamlari ikki marta kamaydi (61- rasm). Agar har kir yuvganda bir xil hajmdagi sovun sarflangani ma’lum bo‘lsa, sovun yana necha marta kir yuvishga yetadi?
242*.Og‘ma prizmada yon qirralariga perpendikular va hamma yon qirralarini kesib o‘tadigan tekislik o‘tkazilgan. Hosil qilingan kesim yuzi Q, yon qirralari esa l ga teng bo‘lsa, prizmaning hajmini toping (62- rasm).
243. Uchburchakli to‘g‘ri prizma asosining tomonlari 4 cm, 5 cm,7 cm ga, yon qirrasi esa asosining katta balandligiga teng. Prizmaning hajmini toping.
244. 63- rasmlarda tasvirlangan ko‘pyoqlarning hajmini hisoblang.
245. Uchburchakli to‘g‘ri prizma asosining yuzi 4 cm2 ga, yon yoqlarining yuzlari 9 cm2, 10 cm2, 17 cm2 ga teng bo‘lsa, uning hajmini toping.
246*.Prizmaning asosi teng yonli uchburchak bo‘lib, uning bir tomoni 2 cm, qolgan ikki tomoni 3 cm ga teng. Prizmaning yon qirrasi 4 cm ga teng va u asos tekisligi bilan 45° li burchak tashkil etadi. Bu prizmaga tengdosh kubning qirrasini toping.
247. Og‘ma prizma asosining tomoni a ga teng bo‘lgan teng tomonli uchburchak. Yon yoqlaridan biri asosiga perpendikular va kichik diagonali s ga teng bo‘lgan rombdan iborat. Prizmaning hajmini toping.
248. Agar to‘rtburchakli to‘g‘ri prizmaning balandligi h, diagonallari asos tekisligi bilan a va b burchaklar tashkil qiladi. Agar asosining diagonallari orasidagi burchak g ga teng bo‘lsa, prizmaning hajmini toping.
249*.Kesimi asosi 1,4 m va balandligi 1,2 m bo‘lgan teng yonli uchburchak shaklidagi suv chiqaruvchi quvurning suv o‘tkazish quvvatini (1 soatda oqib o‘tadigan suv hajmini) hisoblang. Suvning oqish tezligi 2 m/s.
250*.Temiryo‘l ko‘tarmasining kesimi trapetsiya shaklida bo‘lib, uning pastki asosi 14 m, yuqori asosi 8 m va balandligi 3,2 m. 1 km ko‘tarmani qurish uchun qancha kub metr tuproq kerak bo‘ladi?
251*.Tomoni 3,2 cm va qalinligi 0,7 cm bo‘lgan muntazam sakkizburchak shaklidagi yog‘och plitkaning massasi 17,3 g. Yog‘ochning zichligini toping.
252. O‘lchamlari 30×40×50 (cm) bo‘lgan to‘g‘ri burchakli parallelepiped shaklidagi qutidan nechtasini o‘lchamlari 2×3×1,5 m bo‘lgan mashina kuzoviga joylashishi mumkin?
253*.O‘lchamlari 420 mm × 240 mm × 90 mm bo‘lgan to‘g‘ri burchakli parallelepiped shaklidagi, zichligi 7,8 g/cm3 bo‘lgan po‘lat plitalarning nechtasini yuk ko‘tarish quvvati 3 t bo‘lgan yuk mashinasida tashish mumkin?
254. O‘lchamlari 250 mm × 120 mm × 65 mm bo‘lgan to‘g‘ri burchakli parallelepiped shaklidagi, zichligi 1,6 g/cm3 bo‘lgan g‘ishtning nechtasini yuk ko‘tarish quvvati 3 t bo‘lgan yuk mashinasiga yuklash mumkin?
255*.O‘lchamlari 820 mm × 210 mm × 120 mm bo‘lgan to‘g‘ri burchakli parallelepiped shaklidagi, zichligi 7,3 g/cm3 bo‘lgan cho‘yan plitani yuk ko‘tarish quvvati 2 t bo‘lgan ko‘tarma kran yordamida ko‘tarish mumkinmi?
256. Bo‘yi 105 m va ko‘ndalang kesimi o‘lchamlari 30 cm × 40 cm bo‘lgan to‘g‘ri to‘rtburchakdan iborat yog‘ochdan, bo‘yi 3,5 m, eni 20 cm va qalinligi 20 mm bo‘lgan nechta taxta bo‘lagi chiqadi?
257. G‘ishtning o‘lchamlari 25 × 12 × 6,5 (cm). Agar 1 m3 hajmdagi g‘ishtning massasi 1700 kg bo‘lsa, bir dona g‘ishtning massasini gramml arda aniqlang.
258. Sanitariya me’yorlariga ko‘ra, sinfdagi har bir o‘quvchiga 7,5 m3 havo to‘g‘ri keladi. Agar sinfxonaning balandligi 3,5 m va u 28 o‘quvchiga mo‘ljallangan bo‘lsa, sinfxonaning maydonini toping.
259*.Bo‘yi 100 m, eni esa 10 m bo‘lgan to‘g‘ri to‘rtburchak shaklidagi maydonni qalinligi 5 cm bo‘lgan asfalt bilan qoplash kerak. Agar 1 m3 hajmdagi asfaltning massasi 2,4 tonna va bitta yuk mashinasining yuk ko‘tarish quvvati 5 tonna bo‘lsa, bu maydonni asfaltlash uchun nechta mashina asfalt kerak bo‘ladi?
260*.O‘lchamlari 3 cm, 4 cm, 5 cm bo‘lgan, to‘g‘ri burchakli parall e-lepiped shaklidagi temir parchasiga dastgohda ishlov berildi. Bu jarayonda uning har bir qirrasi birdek kamayib, to‘la sirti 42 cm2 ga kamaygani ma’lum. Bu temir parchasining hajmi ishlov berilgandan keyin qanchani tashkil qiladi?
261*.64.a- rasmda cho‘yan quvur kesimi tasvirlangan. Rasmda berilgan ma’lumotlar asosida bir metr uzunlikdagi bunday quvurning massasini aninqlang (cho‘yanning zichligi – 7,3 g/cm3).
262. O‘lchamlari 64.b- rasmda berilgan oltin plitka (yombi) ning massasi 12,36 kg bo‘lsa, uning zichligini aniqlang.
263*.Kanalning ko‘ndalang kesimi asoslari 10 m, 6 m va balandligi 2 m bo‘lgan teng yonli trapetsiyadan iborat (65- rasm). Suv oqimi tezligi 1 m/s bo‘lsa, bir minutda bu kanaldan qancha hajmdagi suv oqib o‘tadi?
264*.Qirrasi 6 cm ga teng bo‘lgan, misdan ishlangan kubning har bir yog‘idan ko‘ndalang kesimi – asosi 2 cm ga teng kvadrat shaklidagi teshiklar o‘yilgan (66- rasm). Agar misning solishtirma zichligi 0,9 g/cm3 bo‘lsa, kubning qolgan qismining massasini toping.
265. To‘g‘ri burchakli parallelepiped shaklidagi metall blok asosining o‘lchamlari 7 cm va 5 cm. Blokning massasi 1285 g va metalning zichligi 7,5 g/cm3 bo‘lsa, blokning balandligini toping.
266. 67- rasmda berilgan ma’lumotlar asosida garajning hajmini toping.
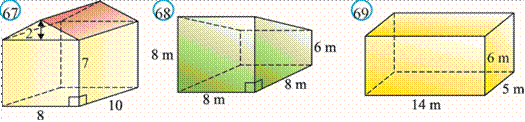
267. Gul o‘stiriladigan katta tuvak chuqurligi 2 fut, kengligi 12 fut va uzunligi 15 fut bo‘lgan to‘g‘ri burchakli parallelepiped shaklida. Tuvakning hajmini toping va kub metrlarda ifodalang (1 fut = 30,48 cm).
268. Yuk ombori 68- rasmda tasvirlangan trapetsiyali prizma shakl ida. Rasmda berilgan ma’lumotlar asosida omborning sig‘imini aniqlang.
269*.69- rasmda qutining o‘lchamlari berilgan. Qutining asoslari 1 kvadrat metri 1000 so‘m, yon yoqlari esa 1 kvadrat metri 2000 so‘m bo‘lgan materialdan ishlangan. Qutini yasashga necha so‘mlik material ketgan?
270. Kubning hajmi V ga teng bo‘lsa, uning diagonalini toping.
271. Katta to‘g‘ri burchakli parallelepipeddan 70- rasmda ko‘rsatilgandek qilib kichik to‘g‘ri burchakli parallelepiped qirqib olingan. Berilgan ma’lumotlar asosida hosil bo‘lgan jismning hajmini toping. 272. 71- rasmda tasvirlangan piramida hajmini toping.
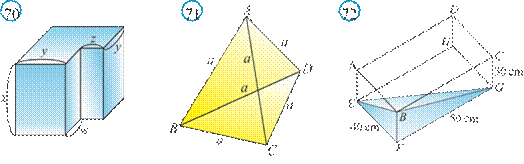
273*.72- rasmda tasvirlangan to‘g‘ri burchakli parallelepiped shaklidagi akvariumda qancha suv bor?
274*.To‘g‘ri burchakli parallelipiped shaklidagi bir xil akvariumlarga
73- rasmda ko‘rsatilgandek, turli sathdagi suv quyilgan. Bu akvariumlarga quyilgan suv hajmlarining nisbati qanday bo‘ladi?
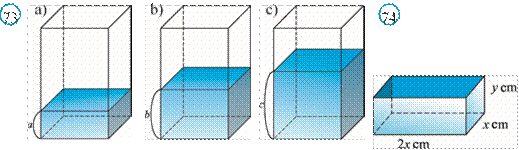
275*. Tatqiqot. Korxona sig‘imi 1 litr, asosining o‘lchamlari nisbati 1:2 bo‘lgan to‘g‘ri burchakli parallelepiped shaklidagi usti ochiq qutilarni ishlab chiqarmoqchi (74- rasm). Qutini tejamli ishlab chiqarish, ya’ni unga ketadigan material eng kam bo‘lishi uchun uning o‘lchamlari qanday bo‘lishi kerak? (x ga turli qiymatlar berib, qutining hajmini toping va ularni taqqoslash bilan yechishga urinib ko‘ring yoki differensial hisob imkoniyatlaridan foydalaning.)
276*. Muammoli vaziyat. Geologlar tosh topib oldilar va uning hajmini taxminan bo‘lsada aniqlashmoqchi. Ular ko‘l yonida turishibdi va ularning ixtiyorida tosh sig‘adigan katta metall bak, bir nechta sig‘imi noma’lum chelaklar va sig‘imi 1 litr bo‘lgan butilka bor. Geologlar bu ishni qanday uddalay olishadi?
8. SILINDRNING SIRTI VA HAJMI
Fazoviy shakllarning yana muhim sinflaridan biri – bu aylanish jismlaridir. Silindr aylanish jismlardan biri bo‘lib, u bilan quyi sinflarda tanishgansiz. Silindr xossalari prizmaning xossalariga o‘xshagani uchun ularni ketma-ket o‘rganamiz.
Tog‘ri to‘rtburchakni bir tomoni atrofida aylantirishdan hosil bo‘lgan jismga silindr (aniqrog‘i, to‘g‘ri doiraviy silindr) deb aytiladi (75- rasm). Bu aylanishda tog‘ri to‘rtburchakning bir tomoni qo‘zg‘alishsiz qoladi. Uni silindrning o‘qi deb ataymiz. To‘rtburchakning bu tomonga qaramaqarshi yotgan tomoni aylanishidan hosil bo‘lgan sirt – silindrning yon sirti, tomonning o‘zi esa silindrning yasovchisi deb ataladi. Tog‘ri to‘rtburchakni qolgan tomonlari bu aylanishda ikkita teng doira hosil qiladi, ularni silindrning asoslari deb ataymiz (76- rasm).
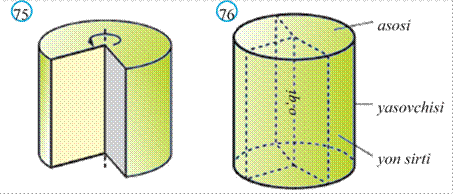
Eslatma. To‘g‘ri to‘rtburchakni bir tomoni atrofida aylantirishdan hosil bo‘lgan jism aslida to‘g‘ri doiraviy silindr deb yuritiladi. Silindr tushunchasi esa keng ma’noda quyidagicha kiritiladi.
Aytaylik, fazoda yassi F1 shakl biror parallel ko‘chirishda F2 shaklga o‘tsin. Bu ikki shakl va mazkur parallel ko‘chirishda bir-biriga o‘tgan nuqtalarni tutashtiruvchi kesmalardan iborat jismga silindr deb ataladi (77- rasm).
Agar parallel ko‘chirish yassi F1 shakl tekisligiga perpendikular bo‘lsa, silindr to‘g‘ri silindr (78.a- rasm) deb, aks holda og‘ma silindr (78.b- rasm) deb yuritiladi.
78.c- rasmda tasvirlangan Piza minorasi og‘ma silindr shaklida.
Agar F1 shakl doiradan iborat bo‘lsa, silindr doiraviy silindr deb ataladi.
To‘g‘ri doiraviy silindrgina aylanma jism bo‘ladi. Kelgusida to‘g‘ri doiraviy silindrlar bilan ish ko‘ramiz va ularni qisqalik uchun silindrlar deb ataymiz.
Silindrning asoslari o‘zaro teng doiralardan iborat bo‘lib, ular parallel tekisliklarda yotadi. Silindrning bir asosi nuqtasidan ikkinchi asosi tekisligiga tushirilgan perpendikular uning balandligi deb ataladi.
Bu parallel tekisliklar orasidagi masofa silindrning balandligiga teng bo‘ladi. Silindrning o‘qi uning balandligi hamdir.
Silindrning yasovchilari esa o‘zaro parallel va teng bo‘ladi. Shuningdek, silindr o‘qi, yasovchilari va balandligi uzunliklari o‘zaro teng bo‘ladi.
Silindrni uning o‘qiga parallel tekislik bilan kesganda hosil bo‘lgan kesim to‘g‘ri to‘rtburchakdan iborat bo‘ladi (79.a- rasm). Uning ikki tomoni silindrning yasovchilari, qolgan ikki tomoni esa mos ravishda asoslarning parallel vatarlaridir.
Xususan, o‘q kesim ham to‘g‘ri to‘rtburchak bo‘ladi. U silindrning o‘qi orqali o‘tgan tekislik bilan kesganda hosil bo‘lgan kesimdir (79.b- rasm).
O‘q kesimlarning diagonallari asos markazlarini tutashtiruvchi kesmaning o‘rtasi Q nuqtadan o‘tadi. Shuning uchun, bu Q nuqta silindrning simmetriya markazidan iborat bo‘ladi (79.c- rasm).
Q nuqtadan o‘tuvchi va silindr o‘qiga perpendikular bo‘lgan tekislik silindrning simmetriya tekisligidan iborat bo‘ladi (80- rasm). Silindrning o‘qidan o‘tuvchi tekisliklar ham uning simmetriya tekisliklari bo‘ladi (81- rasm).

1- masala. Silindr o‘q kesimining yuzi Q ga teng kvadratdan iborat. Silindr asosining yuzini toping.
![]()
![]() Yechish. Kvadratning tomoni Q ga teng. U silindr asosining diametriga teng. Unda silindr
asosining yuzi: S r2 2Q 2 4Q ga teng.
Yechish. Kvadratning tomoni Q ga teng. U silindr asosining diametriga teng. Unda silindr
asosining yuzi: S r2 2Q 2 4Q ga teng. ![]()
Teorema. Silindrning yon sirti asosining aylana uzunligi bilan yasovchisi ko‘paytmasiga teng: Syon = 2πrl.
Mazkur teoremani quyidagi 82- rasm asosida mustaqil isbotlang.
|
Natija. Silindr to‘la sirti uning yon sirti bilan ikkita asosining yuzi yig‘indisiga teng: Sto‘la = Syon + 2Sasos yoki Sto‘la = 2πrl + 2πr2 = 2πr ( l + r ). |
Ixtiyoriy silindr berilgan bo‘lsin. Uning asoslaridan biriga ichki
A1A2…An–1An ko‘pburchakni chizamiz (83- rasm). Ko‘pburchakning
A1, A2, …, An–1 va An uchlari orqali, silindrning A1B1, A2B2, …, An–1Bn–1 va AnBn yasovchilarni o‘tkazamiz hamda yasovchining boshqa B1, B2, …, Bn–1 va Bn uchlarini ketma-ket kesmalar bilan tutashtirib chiqamiz. Natijada
A1A2…An–1An B1B2…Bn–1Bn prizmani hosil qilamiz. Bu prizma berilgan silindrga ichki chizilgan prizma deb ataladi. Silindr esa prizmaga tashqi chizilgan silindr deb yuritiladi. Agar prizma silindrga ichki chizilgan bo‘lsa, unda prizmaning asosi silindr asosiga ichki chizilgan bo‘ladi va prizmaning yon qirralari silindr yon sirtida yotadi.
Ravshanki, agar prizma asosiga tashqi aylana chizish mumkin bo‘lsa, prizmaga tashqi silindr ham chizish mumkin.
Shunga o‘xshash silindrga tashqi chizilgan prizma va prizmaga ichki chizilgan silindr tushunchalari ham kiritiladi (84- rasm). Agar prizma silindrga tashqi chizilgan bo‘lsa, unda prizmaning asosi silindr asosiga tashqi chizilgan bo‘ladi va prizmaning yon yoqlari silindr yon sirtiga urinadi.
Ravshanki, agar prizma asosiga tashqi aylana chizish mumkin bo‘lsa, prizmaga tashqi silindr ham chizish mumkin.
|
Teorema. Silindrning hajmi asosining ko‘paytmasiga teng: V = Sasos ∙ l. |
yuzi |
bilan |
yasovchisi |
Isbot. O‘qi OO1 bo‘lgan silindr berilgan bo‘lsin (85- rasm).
Unga ichki A1 A2 … An–1 An B1 B2 … Bn–1 Bn va tashqi C1 C2 … Cn–1 Cn
D1 D2 … Dn–1 Dn prizmalarni chizamiz. Silindr hajmini V, ichki va tashqi chizilgan prizmalar hajmini V1 va V2 bilan belgilasak, unda V1 < V < V2 qo‘shtengsizlik o‘rinli bo‘ladi. Prizmalar hajmi quyidagi formulalardan topiladi:
V1 = SA1A2 …An–1An ∙ l va V2 = SC1C2…Cn–1Cn ∙ l
Prizmalar asosi tomonlari soni n ni borgan sari oshirib boramiz. Unda ichki chizilgan prizma hajmi oshib boradi, tashqi chizilgan prizmaning hajmi esa kamayib boradi. Agar tomonlar soni n cheksiz kattalashib borsa, bu hajmlar orasidagi farq nolga intiladi. Silindrga ichki va tashqi chizilgan prizmalar hajmi yaqinlashgan son berilgan silindrning hajmi sifatida olinadi.
Bu jarayonda A1A2…An–1An va C1C2…Cn–1Cn ko‘pburchaklar yuzi silindr asosida yotgan doira yuzi S ga yaqinlashadi.
Demak, V = Sasos ∙ l. ![]()
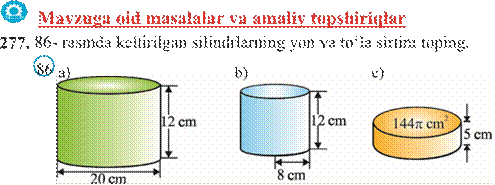
278. Silindr asosining radiusi 6 cm, uning balandligi 4 cm. Silindr o‘q kesimining yuzini hisoblang.
279. Silindr asosining radiusi 2 m, balandligi 3 m. O‘q kesimining diagonalini toping.
280. Silindr asosining yuzi 64 π cm2, uning balandligi 8 cm. Silindr o‘q kesimining yuzini hisoblang.
281. Silindrning o‘q kesimi – yuzi Q ga teng kvadrat. Silindr asosining yuzini toping.
282. Silindrning o‘q kesimi yuzi 36 cm2 bo‘lgan kvadratdan iborat. Silindr yon sirtining yuzini hisoblang.
283. Silindr o‘q kesimining yuzi 4 ga teng. Uning yon sirti yuzini toping.
284. Silindrning balandligi 6 cm, asosining radiusi 5 cm. Silindrning o‘qigaparallel ravishda undan 4 cm masofada o‘tkazilgan kesimning yuzini toping.
285. Silindr asosining radiusi 2 ga, balandligi 3 ga teng. Silindr yon sirtining yuzini toping.
286. Silindr asosining aylana uzunligi 3π ga, balandligi 2 ga teng. Silindrning yon sirti yuzini toping.
287. Silindr yoyilmasining yuzi 24π dm2, silindrning balandligi 4 dm. Uning asosi radiusini toping.
288. Silindr asosining radiusi 5 cm, uning balandligi 6 cm. Silindr o‘q kesimining diagonalini toping.
289. Silindrning balandligi 8 dm, asosining radiusi 5 dm. Silindr tekislik bilan shunday kesilganki, kesimda kvadrat hosil bo‘lgan. Bu kesimdan silindr o‘qigacha bo‘lgan masofani toping.
290*.87- rasmda berilgan silindrning o‘q kesimiga ko‘ra, uning yon va to‘la sirti yuzini toping.
291*.88- rasmda berilgan silindrning yoyilmasiga ko‘ra, uning yon va to‘la sirtining yuzini toping.
292. Silindr asosining radiusi 3 cm, balandligi esa asos radiusidan 2 cm ortiq.
Silindirning hajmini hisoblang.
293. Silindrning hajmi 64 π cm3, balandligi 4 cm. Silindr asosining yuzini hisoblang.
294*.Silindr shaklidagi idishga 2000 cm3 suv solinganda suvning sathi 12 cm ni tashkil qildi. Idishga detal botirilganda esa suv sathi yana 9 cm ga ko‘tarildi. Detal hajmini aniqlang va javobni cm3 larda ifodalang.
295. Silindr shaklidagi idishga 3 litr suv solinganda suvning sathi 15 cm ni tashkil qildi (89-rasm). Idishga detal botirilganda esa suv sathi yana 4 cm ga ko‘tarildi. Detal hajmini aniqlang va javobni cm3 larda ifodalang.
296*.Silindr shaklidagi idishga 4 litr suv solinganda suvning sathi 20 cm ni tashkil qildi (90-rasm). Idishga detal botirilganda esa suv sathi yana 5 cm ga ko‘tarildi. Detal hajmini aniqlang va javobni cm3 larda ifodalang.
297*.91- rasmda silindr shaklidagi yo‘l tekislagich moslamasi tasvirlangan. Rasmda berilganlardan foydalanib, u bir marta aylanganda qancha maydondagi yo‘lni tekislashini aniqlang.
(Eslatma: 1 ft (fut) = 12 in. (dyuym) = 30,48 cm).
298*.92- rasmdagi suv sepishga mo‘ljallangan rezina quvurning ichki diametri 3 cm, tashqi diamerti 3,5 cm, uzunligi esa 20 m bo‘lsa, unga necha lirt suv ketishini toping. Agar rezinaning zichligi 7 g/cm3 ekanligi ma’lum bo‘lsa, bu rezina quvur o‘ramining massasini toping.

299*.93- rasmda yon sirti yarim silindr shaklida bo‘lgan idish berilgan. Agar 1 cm2 yuzali sirtni bo‘yash uchun 6 g bo‘yoq talab etilsa, bu idishning ham ichki, ham tashqi qismini bo‘yash uchun qancha bo‘yoq kerak bo‘ladi? Idishga necha litr suv ketadi?

300*.Silindr shaklidagi idishlardan biri ikkinchisidan ikki marta kengroq, lekin uch marta pastroq (94- rasm). Bu idishlarning qaysi birining sig‘imi katta?
301*.Asosining radiusi 5 cm, balandligi esa 20 cm bo‘lgan silindr shaklidagi apelsin sharbati idishining asoslari metaldan, yon sirti esa kartondan ishlangan (95- rasm). Agar 1 cm2 metall narxi 5 so‘m, 1 cm2 karton narxi esa 2 so‘m bo‘lsa, bu idishni tayyorlash uchun necha so‘mlik material kerak bo‘ladi? Idishga qancha apelsin sharbati ketadi?
302*.Asosining radiusi 1,5 dyuym, balandligi esa 4,25 dyuym bo‘lgan silindr shaklidagi konserva bankasi berilgan (96- rasm). Bankaning to‘la sirti va hajmini toping. Agar 1 cm2 metall narxi 5 so‘m bo‘lsa, bu idishni tayyorlash uchun necha so‘mlik material kerak bo‘ladi? (Eslatma: 1 in. (dyuym) = 2,54 cm.)
303*.Neft saqlanadigan idish (sisterna) balandligi 16 fut, asosining radiusi 10 fut bo‘lgan silindr shaklida. Agar 1 kub fut 7,5 gallonga teng bo‘lsa, bu sisternaning gallonlardagi sig‘imini aniqlang. (Eslatma: 1 amerika galloni = 3,785 litr. 1 amerika barelli = 42 amerika galloni = 159 litr.)
304*.Fermerning yoqilg‘i baki silindr shaklida. Bakning balandligi 6 fut, asosining radiusi 1,5 fut. Bakning gallonlardagi sig‘imini aniqlang.
305. 97- rasmdagi ma’lumotlardan foydalanib, tasvirlangan fazoviy jismlar hajmini aniqlang.
306*.Silindr shaklidagi idishga 6 cm3 suv solindi. Idishga detal to‘liq cho‘ktirilganda, suv sathi 1,5 marta ko‘tariladi. Detall hajmini aniqlang va javobni cm3 larda ifodalang.
307*.Silindr shaklidagi idishdagi suvning sathi 16 cm. Idishga asosining diametri bu idishga qaraganda 2 marta kichik bo‘lgan silindr shaklidagi ikkinchi idish botirilganda undagi suvning sathi qancha bo‘ladi?
![]() 308. Birinchi silindr hajmi 12 m3. Ikkinchi silindrning
balandligi birinchi silindrga qaraganda 3 marta katta, asosining radiusi esa 2
marta kichik. Ikkinchi silindr hajmini toping.
308. Birinchi silindr hajmi 12 m3. Ikkinchi silindrning
balandligi birinchi silindrga qaraganda 3 marta katta, asosining radiusi esa 2
marta kichik. Ikkinchi silindr hajmini toping.
309*.Silindr shaklidagi idish ikkinchisidan 2 marta baland, lekin 1,5 marta kengroq. Bu idishlar hajmlarining nisbatini hisoblang.
310. 98- rasmda tasvirlangan fazoviy jism hajmini toping.
311. 99- rasmda tasvirlangan silindr bo‘lagining hajmini toping.
313. To‘g‘ri burchakli parallelepiped asosining radiusi va balandligi 1 ga teng bo‘lgan silindrga tashqi chizilgan (101- rasm). Parallelepiped hajmini toping.
314. To‘g‘ri burchakli parallelepiped asosining radiusi 4 ga teng bo‘lgan silindrga tashqi chizilgan (102- rasm). Parallelepiped hajmi 16 ga teng bo‘lsa, silindrning balandligini toping.
315. To‘g‘ri prizmaning asosi katetlari 6 va 8 bo‘lgan to‘g‘ri burchakli uchburchakdan iborat, yon qirralari esa 5 ga teng (103- rasm). Bu prizmaga tashqi chizilgan silindr hajmini toping.
316. To‘g‘ri prizmaning asosi – tomoni 2 ga teng bo‘lgan kvadratdan iborat, yon qirralari esa 2 ga teng. Bu prizmaga tashqi chizilgan silindr hajmini toping.
317. To‘rtburchakli to‘g‘ri prizma asosining radiusi 2 ga teng bo‘lgan silindrga tashqi chizilgan (104- rasm). Prizma yon sirtining yuzi 48 ga teng bo‘lsa, silindrning balandligini toping.
318. Muntazam to‘rtburchakli prizma asosining radiusi va balandligi 1 ga teng bo‘lgan silindrga tashqi chizilgan (105- rasm). Prizma yon sirtining yuzini toping.
319. ![]() Uchburchakli to‘g‘ri prizma asosining radiusi 3 ga va balandligi 2
ga teng bo‘lgan silindrga tashqi chizilgan (106- rasm). Prizma yon
sirtining yuzini toping.
Uchburchakli to‘g‘ri prizma asosining radiusi 3 ga va balandligi 2
ga teng bo‘lgan silindrga tashqi chizilgan (106- rasm). Prizma yon
sirtining yuzini toping.
320. ![]() Uchburchakli muntazam prizma asosining radiusi 2 3 ga va balandligi 2 ga teng
bo‘lgan silindrga ichki chizilgan (107- rasm). Prizma yon sirtining yuzini
toping.
Uchburchakli muntazam prizma asosining radiusi 2 3 ga va balandligi 2 ga teng
bo‘lgan silindrga ichki chizilgan (107- rasm). Prizma yon sirtining yuzini
toping.
321. ![]() Oltiburchakli muntazam prizma asosining radiusi 3 ga va balandligi 2 ga teng
bo‘lgan silindrga tashqi chizilgan (108- rasm). Prizma yon sirtining yuzini
toping.
Oltiburchakli muntazam prizma asosining radiusi 3 ga va balandligi 2 ga teng
bo‘lgan silindrga tashqi chizilgan (108- rasm). Prizma yon sirtining yuzini
toping.
322*. 109- rasmda tasvirlangan detalning hajmini toping.
323*.Uzunligi 10 m, asosining diametri 1 m bo‘lgan silindr shaklidagi quvurning tashqi sirtini 1 mm qalinlikdagi bo‘yoq bilan bo‘yash uchun qancha bo‘yoq kerak bo‘ladi?
324*.110- rasmda tasvirlangan tirsakli quvurning: a) yon sirtining yuzini;
b) hajmini toping (π ≈ 3 deb oling).
325*. Cho‘yan quvurning uzunligi 2 m, tashqi diametri 20 cm. Quvur devorining qalinligi 2 cm va cho‘yannning solishtirma zichligi 7,5 g/cm3 bo‘lsa, uning massasini toping.
326*.111- rasmdan foydalanib, og‘ma silindr uchun S ∙ h = Q ∙ l tenglik o‘rinli bo‘lishini asoslang.
327*.112- rasmda tasvirlangan silindr sirtidan A nuqtadan B nuqtaga olib boradigan eng qisqa yo‘lning uzunligini toping. (Ko‘rsatma: silindr yoyilmasidan foydalaning.)
Abu Rayhon Beruniyning “Astronomiya san’atidan boshlang‘ich ma’lumot beruvchi kitob” (qisqacha “Astronomiya”) nomli asarining geometriyaga tegishli qismida stereometriyaga kirish sifatida fazoviy shakllarning quyidagi ta’riflari keltiriladi.
Kub – jismiy shakl bo‘lib, nardning soqqasiga o‘xshaydi, oltita tomonidan oltita kvadrat bilan chegaralangan.
![]() Prizma – mujassam shakl bo‘lib, yon tomonidan Abu Ali ibn Sino kvadrat
yoki to‘g‘ri to‘rtburchak shaklidagi tekisliklar bilan, osti va ustidan ikkita
uchburchak bilan chegaralangan.
Prizma – mujassam shakl bo‘lib, yon tomonidan Abu Ali ibn Sino kvadrat
yoki to‘g‘ri to‘rtburchak shaklidagi tekisliklar bilan, osti va ustidan ikkita
uchburchak bilan chegaralangan.
Beruniy bergan bu ta’rifda prizmaning xususiy holi, ya’ni uchburchakli prizmaning ta’rifi keltirilgan.
Abu Rayhon Beruniyning “Qonuni Ma’sudiy” kitobi 1037- yilda yozilgan bo‘lib, unda parallelepiped, prizmaning hajmlarini topish qoidalari: “Agar jism to‘rtburchakli bo‘lmasdan yoki boshqa xil bo‘lsa, uning o‘lchami quyidagicha: uning yuzini bilgin, uni
chuqurlikka ko‘paytirgin, natijada hajm hosil bo‘ladi” G‘iyosiddin tarzda berilgan. al Koshiy
Abu Ali ibn Sino “Donishnoma” nomli asarining “Geometrik jismlarga oid negizlar” bobida jismning va uchburchakli prizmaning ta’rifini beradi hamda ikki prizmaning o‘zaro teng bo‘lish shartlarini bayon qiladi. Ibn Sino prizmani quyidagicha ta’riflaydi: “Prizma ikkita uchburchakli tekis shakllar va tomonlari o‘zaro parallel uchta tekis shakllar bilan chegaralangan jismdir”.
G‘iyosiddin Jamshid ibn Ma’sud al- Koshiyning “Hisob kitobi” nomli asarida sirtlar yuzlarini va jismlarning hajmlarini hisoblashning ko‘plab qoidalari keltirilgan. U matematika, geometriya, trigonometriya, mexanika va astronomiya kabi fanlarni chuqur bilganligi uchun Ulug‘bekning e’tibori va hurmatiga sazovor bo‘lgan. Al- Koshiy ko‘pburchaklar bilan bir qatorda prizmalar, piramidalar, silindrlar, konuslar, kesik konuslarni ham tadqiq qilgan.
1. Kubning nechta simmetriya tekisligi mavjud? A) 8; B) 9; C) 7; D) 10.
![]()
2. Agar kub diagonal kesimining yuzi 2√2 ga teng bo‘lsa, uning hajmini toping.
![]()
A) 2√2; B) √7; C) 4√2; D) 5√2.
3. To‘g‘ri burchakli parallelepiped asosining tomonlari 7 cm va 24 cm. Parallelepipedning balandligi 8 cm. Diagonal kesimining yuzini toping. A) 168; B) 1344; C) 100; D) 200.
4. Muntazam to‘rtburchakli prizmaning diagonali 4 ga teng bo‘lib, yon yog‘i bilan 300 li burchak tashkil qiladi. Prizmaning yon sirtini toping.
![]()
A) 16√2; B) 16; C) 18; D)18√2.
![]()
5. Muntazam to‘rtburchakli prizma asosining tomoni √2 ga, diagonali bilan yon yog‘i orasidagi burchak esa 300 ga teng. Prizmaning hajmini toping.
![]()
A) 8√2; B) 4; C) 16; D) 4√2.
6. Prizmaning jami qirralari 36 ta bo‘lsa, uning nechta yon yog‘i bor? A) 12; B) 16; C) 9; D) 10.
7. Og‘ma prizmaning yon qirrasi 20 ga teng va asos tekisligi bilan 300° li burchak hosil qiladi. Prizmaning balandligini toping.
![]()
A) 12; B) 10√3; C) 10; D) 10√2.
8. Uchburchakli to‘g‘ri prizma asosining tomonlari 15, 20 va 25 ga, yon qirrasi asosining balandligiga teng. Prizmaning hajmini toping. A) 600; B) 750; C) 1800; D) 1200.
9. Muntazam oltiburchakli prizmaning eng katta diagonali 8 ga teng va u yon qirrasi bilan 300° li burchak hosil qiladi. Prizmaning hajmini toping. A) 72; B) 64; C) 76; D) 80.
10. O‘q kesimining yuzi 10 ga teng bo‘lgan silindr yon sirtining yuzini toping.
A) 10π; B) 20π; C) 30π; D) 15π.
11. Silindrning balandligi 8 ga yon sirti yoyilmasining diagonali 10 ga teng. Silindr yon sirtining yuzini toping.
A) 48; B) 48π; C) 24; D) 48π.
12. Tomonlari 2 va 4 ga teng bo‘lgan to‘g‘ri to‘rtburchak o‘zining katta tomoni atrofida aylandi. Hosil bo‘lgan jismning to‘la sirtini toping. A) 22π; B) 23π; C) 24π; D) 20π.
13. Silindrning yon sirti yuzi 72 π ga teng va u yoyilganda hosil bo‘lgan to‘g‘ri to‘rtburchak diagonali asosi bilan 45o burchak tashkil qiladi. Silindr asosining radiusini toping. A) 5; B) 4; C) 6; D) 8.
14. Silindr asosining radiusi ikki marta orttirilsa, uning hajmi necha marta ortadi?
A) 4; B) 2; C) 3; D) 6.
15. Silindrning hajmi 120π ga, yon sirti 60π ga teng. Silindr asosining radiusini toping.
A) 4; B) 5; C) 6; D) 4; 2.
16. Silindrning balandligi 5 ga, asosiga ichki chizilgan muntazam
![]()
uchburchakning tomoni 3√3 ga teng. Silindrning hajmini toping. A) 25π; B) 35π; C) 45π; D) 40π.
17. Silindrning o‘q kesimi diagonali 12 ga teng bo‘lgan kvadratdan iborat. Uning hajmini toping.
![]()
A) 108√2π; B) 54√2π; C) 36√2π; D) 216√2π.
18. Silindrning to‘la sirti 24π ga, yon sirti esa 6π ga teng. Shu silindrning hajmini toping.
A) 7π; B) 11π; C) 8π; D) 9π.
328. ABCDA1B1C1D1 to‘g‘ri burchakli parallelepipedda (113- rasm)
![]()
DC1=√40, DC = 2, PABCD=10. Parallelepipedning diagonalini toping.
329. ABCDA1B1C1D1 to‘g‘ri burchakli parallelepiped. 114- rasmda berilgan ma’lumotlarga ko‘ra B1C1 qirraning uzunligini toping.
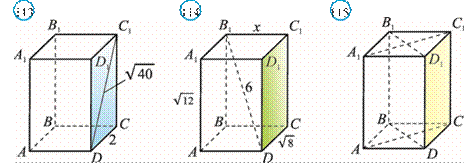
330. To‘g‘ri prizmaning asosi ABCD romb (115- rasm). Prizmaning diagonal kesimlari yuzi 60 va 80 ga, balandligi esa 10 ga teng. Prizmaning yon sirtini toping.
331. To‘g‘ri prizmaning asosi ABCD romb. Prizmaning diagonal kesimlari yuzi 24 va 32 ga, balandligi esa 4 ga teng. Prizmaning yon sirtini toping.
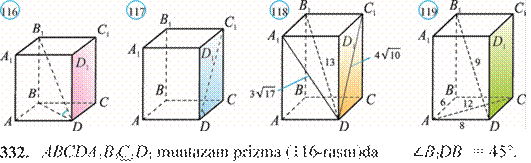
Sto‘la= 32(2√2+1). AD ni toping.
333. ABCDA1B1C1D1 muntazam prizma (117-rasm)da ![]() C1DC = 60°,
C1DC = 60°,
![]()
Sto‘la= 128(2√3 +1). AD ni toping.
334. ABCDA1B1C1D1 to‘g‘ri burchakli parallelepiped (118- rasm)da DB1= 13,
![]()
DA1= 3√17, DC1 = 4√10. Parallelepiped yon sirtining yuzini toping.
335. ABCDA1B1C1D1 to‘g‘ri parallelepiped (119- rasm)da AB = 6, AD = 8, DB1 = 9. Parallelepiped yon sirtining yuzini toping.
336. K nuqta BC qirraning o‘rtasi (120- rasm). ABKA1B1K1 prizma hajmining ABCDA1B1C1D1 parallelepiped hajmiga nisbatini toping.
337. N va M nuqtalar parallelepiped qirralarining o‘rtalari (121- rasm). AA1B1NDD1C1M prizma hajmining ABCDA1B1C1D1 parallelepiped hajmiga nisbatini toping.
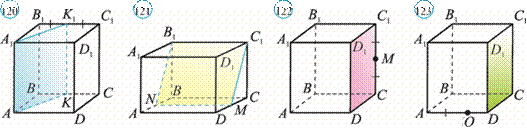
338. To‘rtburchakli muntazam prizma yon sirtining yuzi 72 cm2 ga, asosining yuzi esa 64 cm2 ga teng. Prizmaning hajmini toping.
339. To‘rtburchakli muntazam prizma asosining perimetri 12 cm, yon yog‘ining perimetri esa 18 cm ga teng. Prizmaning hajmini toping.
340. Kub berilgan (122- rasm). CM = MC1 va ADM tekislik kubni ikki bo‘lakka ajratadi. Kubning katta bo‘lagi hajmining kichik bo‘lagi hajmiga nisbatini toping.
341*.Kub berilgan (123- rasm). AO : OD = 2 : 1 va BB1O tekislik kubni ikki bo‘lakka ajratadi. Agar kubning kichik bo‘lagi hajmi 6 ga teng bo‘lsa, kubning hajmini toping.
342*.To‘rtburchakli muntazam prizmaning balandligi 8 ga, diagonalining asos tekisligiga qiyaligi 45° ga teng (124- rasm). Prizmaning hajmini toping.
![]()
343*.To‘rtburchakli muntazam prizmada asosining tomoni 2√6 ga, diagonali asos tekisligi bilan 30° li burchak tashkil qiladi (125- rasm). Prizmaning hajmini toping.
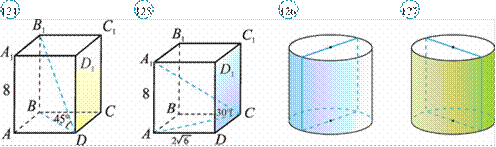
344. Silindr yon sirtining yuzi 91π ga teng (126- rasm). Silindr o‘q kesimining yizini toping.
345. Silindr o‘q kesimi yuzi 173 ga teng bo‘lgan kvadrat (127- rasm). Silindr yon sirtining yuzini toping.
346. Silindr balandligi 24 ga, o‘q kesim diagonali 26 ga teng. Silindr hajmini toping.
347. Silindr o‘q kesimi yuzi 10 ga. Asos aylanasining uzunligi 8 ga teng. Silindr hajmini toping.
348. Silindr radiusi 3 ga, yon sirtining yuzi 200 ga teng. Silindr hajmini toping.
1. Ikkiyoqli burchakning A nuqtasi uning qirrasidan 10 cm, yog‘idan 5 cm uzoqlikda joylashgan. Ikkiyoqli burchakning gradus o‘lchovini toping.
2. ![]() Oltiburchakli muntazam prizmaning barcha qirralari 2 ga teng
bo‘lsa, uning to‘la sirtining yuzini toping.
Oltiburchakli muntazam prizmaning barcha qirralari 2 ga teng
bo‘lsa, uning to‘la sirtining yuzini toping.
3. Asosining diamerti 18 m va balandligi 7 m bo‘lgan silindr shaklidagi sisterna neft bilan to‘ldirilgan. Agar neftning zichligi 0,85 g/cm3 bo‘lsa, bu sisternadagi neftning massasi necha tonna?
4. Har bir qirrasi uzunligi 4 cm ga teng bo‘lgan muntazam oltiburchakli prizmaga ichki chizilgan silindr hajmini toping.
5. (Yaxshi o‘zlashtiradigan o‘quvchilar uchun qo‘shimcha masala.) 128- rasmda o‘lchamlar mm larda berilgan detalning to‘la sirti va hajmini toping.
Trigonometrik funksiyalarning taqribiy qiymatlari jadvali
|
A |
sin A |
tg A |
A |
sin A |
tg A |
A |
sin A |
tg A |
|
0о |
0 |
0 |
30о |
0,50 |
0,58 |
60о |
0,87 |
1,73 |
|
1о |
0,0175 |
0,0175 |
31о |
0,52 |
0,60 |
61о |
0,87 |
1,80 |
|
2о |
0,035 |
0,035 |
32о |
0,53 |
0,62 |
62о |
0,88 |
1,88 |
|
3о |
0,05 |
0,05 |
33о |
0,54 |
0,65 |
63о |
0,89 |
1,96 |
|
4о |
0,07 |
0,07 |
34о |
0,56 |
0,68 |
64о |
0,90 |
2,02 |
|
5о |
0,09 |
0,09 |
35о |
0,57 |
0,70 |
65о |
0,91 |
2,15 |
|
6о |
0,10 |
0,11 |
36о |
0,59 |
0,73 |
66о |
0,91 |
2,25 |
|
7о |
0,12 |
0,12 |
37о |
0,60 |
0,75 |
67о |
0,92 |
2,36 |
|
8о |
0,14 |
0,14 |
38о |
0,62 |
0,78 |
68о |
0,93 |
2,48 |
|
9о |
0,16 |
0,16 |
39о |
0,63 |
0,81 |
69о |
0,93 |
2,61 |
|
10о |
0,17 |
0,18 |
40о |
0,64 |
0,84 |
70о |
0,94 |
2,78 |
|
11о |
0,19 |
0,19 |
41о |
0,66 |
0,87 |
71о |
0,95 |
2,90 |
|
12о |
0,21 |
0,21 |
42о |
0,67 |
0,9 |
72о |
0,95 |
3,08 |
|
13о |
0,23 |
0,23 |
43о |
0,68 |
0,93 |
73о |
0,96 |
3,27 |
|
14о |
0,24 |
0,25 |
44о |
0,69 |
0,97 |
74о |
0,96 |
3,49 |
|
15о |
0,26 |
0,27 |
45о |
0,71 |
1,00 |
75о |
0,97 |
3,73 |
|
16о |
0,28 |
0,29 |
46о |
0,72 |
1,04 |
76о |
0,97 |
4,01 |
|
17о |
0,29 |
0,31 |
47о |
0,73 |
1,07 |
77о |
0,97 |
4,33 |
|
18о |
0,31 |
0,32 |
48о |
0,74 |
1,11 |
78о |
0,98 |
4,71 |
|
19о |
0,33 |
0,34 |
49о |
0,75 |
1,15 |
79о |
0,98 |
5,15 |
|
20о |
0,34 |
0,36 |
50о |
0,77 |
1,19 |
80о |
0,98 |
5,67 |
|
21о |
0,36 |
0,38 |
51о |
0,78 |
1,23 |
81о |
0,99 |
6,31 |
|
22о |
0,37 |
0,40 |
52о |
0,79 |
1,28 |
82о |
0,99 |
7,12 |
|
23о |
0,39 |
0,42 |
53о |
0,80 |
1,33 |
83о |
0,992 |
8,14 |
|
24о |
0,41 |
0,45 |
54о |
0,81 |
1,38 |
84о |
0,994 |
9,51 |
|
25о |
0,42 |
0,47 |
55о |
0,82 |
1,43 |
85о |
0,996 |
11,43 |
|
26о |
0,44 |
0,49 |
56о |
0,83 |
1,48 |
86о |
0,998 |
14,30 |
|
27о |
0,45 |
0,51 |
57о |
0,84 |
1,54 |
87о |
0,999 |
19,08 |
|
28о |
0,47 |
0,53 |
58о |
0,85 |
1,60 |
88о |
1,00 |
28,64 |
|
29о |
0,48 |
0,55 |
59о |
0,86 |
1,66 |
89о |
1,00 |
57,29 |
JAVOBLAR
3. A(5; 7; 10), B(4; –3; 6), C(5; 0; 0), D(4; 0; 4), E(0; 5; 0), F(0; 0; –2). 6. (3; 2; 0),
![]()
(3; 0; 4), (0; 2; 4). 8. √26. 9. a) 3, 3, 3; b) 3√2, 3√2, 3√2; c) 3√2. 10. 2, 3, 1. 11. (3; 3; 3),
(–3; 3; 3), (3; –3; 3), (3; 3; –3), (–3; –3; 3), (–3; 3; –3), (3; –3; –3), (–3; –3; –3). 12. O(0;0; 0),
B(2; 0; 0), A(2; 2; 0), C(0; 2; 0), O1(0; 0; –2), B1(2; 0; –2), A1(2; 2; –2), C1(0; 2; –2).
![]()
13. D nuqta. 14. 3√6. 15. Yo‘q. 17. c) teng yonli, P=6 (1+√3), S = 9√2.
18. (–0,25; 0,25; 0). 19. D1(1; –1; 1), A1(1; 1; –1), B1(–1; 1; –1), D1(1; –1; –1).
21. x2+y2+z2=25, x2+y2+z2≤25. 22. (x–1)2+(y–2)2+(z–4)2=9; (x–1)2+(y–2)2+(z–4)2≤9.
23. (x+2)2+(y–3)2+(z–4)2=9. 25. 1)(0; 1; 0); 2) (1; 1; 1); 3) (0; 0; 2), 4) (–0,7; 0,1; 0,6);
![]() 17
17
5) (2√3; 1,5; 1). 28. A(5;–4;0), B(–7;5;6), 31. K0;
5;− ![]() . 32. a) D(–1; –3;
–9).
. 32. a) D(–1; –3;
–9).
2
33. a) M(–1; 2; 0); c) M![]() ; 0).
; 0). ![]() ; b) 30°; 30°; 120°;
c)
; b) 30°; 30°; 120°;
c)
![]()
![]()
![]() 2√3. 38. MK= (5; 4; 10), B(4;
–3; 6), C(5; 0; 0), D(4; 0; 4). 40. OA=(1; 1; 1),
OB=(–1; 0; 1), OC=(0; 1; 1), BO =(1; 0; –1), CO=(0;
–1; –1), AB =(–2; –1; 0).
2√3. 38. MK= (5; 4; 10), B(4;
–3; 6), C(5; 0; 0), D(4; 0; 4). 40. OA=(1; 1; 1),
OB=(–1; 0; 1), OC=(0; 1; 1), BO =(1; 0; –1), CO=(0;
–1; –1), AB =(–2; –1; 0).
42. a) AB =(2; 5; 3), b) AB =(4; –6; 2). 43. |a|=√3; |b|=2√5, |c|=√14, |d|=√30. 44. ±3.
45. a) a(3; 6; –3), b) a(–3; –6; 3). 46. a) 1 yoki –1; b) 3 yoki –1; c) 2 yoki –4; d) 3 yoki 5/3. 48. D(–2; 0; 1). 52. a) D(3; 0; 0). 56. c(–3; –4; 8), |c|=√89; 2) c(4; 5; 5),
![]()
![]() |c|=√66.
57. c(–3; 4; 0),
|c|=5; 2) c(0; 2; 6), |c|=2√10. 59. a=i–j+k,
b=2j–4k, c=2i+3j–k, d=i+2j+5k. 60. √59,
√219, √122, √918. 63. AC = AO + OC = 4i + 2k, AC(–4; 0; 2); CB = CO + OB = 2k
+ 9j, CB (0; 9; 2); AB = AO + OB = –4i + 9j,
|c|=√66.
57. c(–3; 4; 0),
|c|=5; 2) c(0; 2; 6), |c|=2√10. 59. a=i–j+k,
b=2j–4k, c=2i+3j–k, d=i+2j+5k. 60. √59,
√219, √122, √918. 63. AC = AO + OC = 4i + 2k, AC(–4; 0; 2); CB = CO + OB = 2k
+ 9j, CB (0; 9; 2); AB = AO + OB = –4i + 9j,
AB(–4; 7; 0). 65. ≈180N. 66. a) 60°; b) 30°; c) 90°; d) 60°; e) 45°. 67. a) –6; b) 3; c) –6; d) 3. 68. a) 40°; b) 140°; c) 150°. 69. a) 30; b) 3; c) 15; d) –28. 70. a) 1/3; b) –1; c) 2; d) 4.
![]()
![]() 71. a) 16. 75. a) 1; b) 0. 76. BF =2(DO–DC).
AC –AB ).
71. a) 16. 75. a) 1; b) 0. 76. BF =2(DO–DC).
AC –AB ). ![]() )–AD .
)–AD .
83. a) (1; –1; 7); b) (–2; 3; 1); c) (0; –4; 4). 84. p(–1; 5; 3). 86. B(–8; 4; 1). 88. (2; –5; 9); (–2; –2; 7); (6; –12; 2). 93. Oxz tekislikka nisbatan. 100. (0; –3; 1). 106. a) 36 cm; b) 48 cm; c) 6 cm; d) 4 cm. 110. a) B(–5; 7,5; 12,5); b) B(5; –7,5; –12,5); c) B(–0,5; 0,75; 1,25);
d) B(0,5; –0,75; –1,25). 111. a) B(–2,5; 1; 3); b) B(– 7; 2; 6). 112. a) O1(0; 0; 0), A1(–4; 0; 0), B1(0; –4; 0), C1 (0; 0; –4); b) O1(–4; 0; 0), A1(4; 0; 0), B1(–4; 8; 0), C1 (–4; 0; 8). 115. (2;–3; 3).
116. –3. 117. (7; 1; 2). 118. (1; –2; 3). 119. (–1; –2; –3). 120. (1; 2; –3). 121. (–2; –3; –5). 122. D(0; 9;–7). 123. C(2; 0;–8). 124. 19. 125. (–7; 7; –7). 126. (1; 2; 1). 127. (–2; 7; 1).
128. ±2. 129. ±3. 130. 13. 131.r 10. r 132.r 9. 133. 0. 134. –2. 135. 1. 136. 4. 137. 90°. 138. 4.
139. –4. 140. –2; 4. 141. 8i + 9 j − 4k .
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
C |
D |
D |
B |
D |
B |
B |
A |
A |
D |
B |
B |
B |
C |
A |
C |
B |
D |
1- nazorat ishi javobi
1) (1; 2; -3); 2) 13; 3) √2; 4) 90°; 5) 1.
142. 47°, 133°, 47°, 133°. 143. 128°. 144. 80°. 145. 90°. 146. 5 cm, 5 cm. 147. 12 cm. 148. 5 cm. 152. 45°. 153. 45°. 154. 80°. 159. 60°, 45°. 165. a) 4, 10; b) 5, 12. 166. Yo’q. 170. 6, kub. 171. 15 ta. 172. 9 ta. 173. 180 ta. 174. 24 cm2. 175. 44 cm2. 176. 76,8 cm2. 177. 17,64 cm. 178. 4√3cm2 , 4 cm. 179. 124 dm2. 180. 20 m2, 30 m2. 181. 8 cm, 8 cm.
182. 13 cm, 9 cm. 184. 4500 cm2. 185. 7,5. 186. 4. 187. 480 cm2. 188. 5√2. 189. 45 cm2. 190. 144. 191. a)18; b)76; c) 110; d) 132; e) 48; f) 96; g) 124. 192. a) 146; b) 126; c) 108; d) 146. 193. 84 cm. 194.3√2 cm2. 195. 216 cm2. 196. a) 58; b) 62; c) 94. 197. a) 38; b) 92; c) 48. 198. ≈68 m2. 199. 104 cm. 200. 68 cm2. 201. 78 cm2. 204. 5120 cm3. 207. 144. 209. 8. 210. 5. 211. 6. 212. 3. 213.
(S–ab)ab
24.
214. 2. 215. 8. 216. 8. 217. 72. 218. 4. 219. 27 litr. 220. 4. 221. 60 cm2. 222. ![]() . 4(a+b)
. 4(a+b)
223. 30 m. 224. 1200. 225. a) 4; b) 40; c) 71; d) 88; e) 18; f) 33; g) 78. 226. a) 90; b)
77; c) 54; d) 96. 227. 6 m3. 228. a) 21; b) 26; c) 58. 230. 6 m![]() .
.
![]()
![]()
![]()
![]() 233. 2√sin3asin3a. 234. abc√–cos2a. 235. a) a2b√3 ; b) a2b; c) 3060 4
233. 2√sin3asin3a. 234. abc√–cos2a. 235. a) a2b√3 ; b) a2b; c) 3060 4
![]() m3. 238. 3 cm
m3. 238. 3 cm![]() 1 marta. 243. 24 cm3. 245. 12 cm3. 246. 2 cm.
1 marta. 243. 24 cm3. 245. 12 cm3. 246. 2 cm.
![]() 247. ac√[7]2a2–3c2. 248. h3sing . 249. 6048 m3/soat. 250. 35200 m3. 251. 0,5 g/cm3.
247. ac√[7]2a2–3c2. 248. h3sing . 249. 6048 m3/soat. 250. 35200 m3. 251. 0,5 g/cm3.
8 2tgatgb
252. 150 ta. 253. 42 ta. 254. 961 ta. 255. 13 ta. 256. 90 ta. 257. 3315 g.
258. 60 m2. 259. 24 ta. 260. 24 cm3. 261. 1927,2 g. 262. 1927,2 g. 263. 960 m3. 264. 144 g. 265. 19,3125 g/cm3. 266. 440 m3. 267. 0,0127 m3. 271. (y+w+z)yx. 274. a:b:c. 277. 240π cm2 , 280π cm2. 278. 48 cm2. 279. 5 cm. 280. 128 cm2. 281. πQ/4. 282. 36π cm2.
![]()
283. 4π. 284. 36 cm2. 285. 12π. 286. 64. 6. 287. 3 dm. 288. 2√34 cm. 289. 3 dm. 290. 200π, 250π. 291. 50, 50 +50/π. 292. 45π cm3. 293. 16π cm2. 294. 1500 cm3.
295. 800 cm2. 296. 1000 cm2. 297. 5574 cm2, 1824 cm2. 298. 1375π cm3, 11,375 kg. 299. 141900 g, 310860 cm2. 300. Birinchisining. 301. 2041 so‘m, 15700 cm2.
302. 349,45 cm2, 492 cm3, 1747 so‘m. 303. 37680 gallon. 304. 318 gallon. 306. 3 cm3. 307. 4 cm . 308. 9 m3. 309. 1,125. 311. a) 45π; b) 3,75π; c) 144π. 312. a) 14π; b) 937,5π. 313. 4. 314. 0,25. 315. 125π. 316. 4π. 317. 3. 318. 8. 319. 36. 320. 36. 321. 24.
322. ≈30 m3. 323. ≈3000 cm3. 324. a) ≈1050 cm2; b) ≈2250 cm3. 325. ≈162 kg. 328. 7. 329. 4. 330. 200. 331. 160. 332. 4. 333. 8. 334. 168. 336. 1/3. 337. 1/3. 338. 144 m3.
339. 56 cm3. 340. 6. 341. 2. 342. 256. 343. 96. 344. 91. 345. 173 π. 346. 600π. 347. 20.
348. 300.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|
B |
A |
D |
A |
B |
A |
C |
C |
A |
A |
A |
C |
C |
A |
A |
C |
A |
D |
Darslikni tuzishda foydalanilgan va qo‘shimcha o‘rganishga tavsiya etilayotgan o‘quv-uslubiy adabiyotlari va elektron resurslar
1. А.В. Погорелов “Геометрия 10–11”, учебник, Москва. “Просвешение”, 2009.
2. Л. А. Латотин, Б. Д. Чеботаревский. “Математика 11”, учебник, Минск, 2013.
3. И.М. Смирнова, В.А. Смирнов Геометрия. 10–11 класс. учебник, Москва, 2008
4. О.Я. Билянина и др. “Геометрия 11” учебник, Киев, “Генеза”, 2010.
5. Daniel C.Alexander, Elementary geometry for college students, Canada, Brooks/ Cole, Cengage Learning, 2011.
6. Mal Coad and others, Mathematics for the international students, Haese and Harris publocations, Australia, 2010.
7. Norjigitov X., Mirzayev Ch. Stereometrik masallarni yechish. Akademik litseylar uchun o‘quv qo‘llanma. –T., 2004.
8. Israilov I., Pashayev Z. Geometriya. Akademik litseylar uchun o‘quv qo‘llanma.
II qism. –T.: O‘qituvchi, 2005.
9. http://www.uzedu.uz – Xalq ta’limi vazirligining axborot ta’lim portali.
10. http://www.eduportal.uz – Multimedia markazi axborot ta’lim portali.
11. http://www.ixl.com – Masofadan turib o‘qitish sayti (ingliz tilida).
12. http://www.mathkang.ru – “Kenguru” xalqaro matematik tanlov sayti (rus tilida).
13. http://www.khanakademy.org – “Xon akademiyasi” masofaviy ta’lim sayti (ingliz tilida).
14. http://www.brilliant.org – Matematikadan masofaviy ta’lim sayti (ingliz tilida).
I BOB. FAZODA KOORDINATALAR SISTEMASI VA VEKTORLAR
1. Fazoda dekart koordinatalari sistemasi ..................................... 113
2. Fazoda vektorlar va ular ustida amallar ..................................... 122
3. Fazoda almashtirishlar va o‘xshashlik ...................................... 133
4. Bobni takrorlashga doir amaliy mashqlar .................................. 142
II BOB. PRIZMA VA SILINDR
5.Ko‘pyoqli burchaklar va ko‘pyoqlar .......................................... 146
6. Prizma va uning sirti ................................................................. 153 7. Prizmaning hajmi ...................................................................... 161
8. Silindrning sirti va hajmi ........................................................... 172
9. Bobni takrorlashga doir amaliy mashqlar ................................. 184
Algebra va analiz asoslari: M.A. Mirzaahmedov, Sh.N. Ismailov, A.Q. Amanov.
Geometriya: B.Q. Xaydarov.
ALGEBRA VA ANALIZ ASOSLARI,
GEOMETRIYA
I QISM
O‘rta ta’lim muassasalarining 11-sinfi va o‘rta maxsus, kasb-hunar ta’limi muassasalari o‘quvchilari uchun darslik
1- nashr
Muharrirlar: N. Gayipov
M. Raemov
Texn. Muharrir: A. Abdusalomov
Kompyuterda sahifalovchi: S. G‘ofurov
Nashriyot litsenziyasi AI № 296. 22.05.2017 Bosishga ruxsat etildi 28.05.2018. Bichimi 70×1001/16
“TimesNewRoman” garniturasi.
Hajmi: 12,0 bosma tab. Nashr tab. 11,0.
Adadi 433091 nusxada
Original-maket “Zamin Nashr” MCHJ da tayyorlandi. 100053, Toshkent sh.
Bog‘ishamol ko‘chasi, 160. Tel: 235 44 82 Buyurtma № 18-333.
O‘zbekiston matbuot va axborot agentligi "O‘ZBEKISTON" nashriyot-matbaa ijodiy uyi 100011, Toshkent sh., Navoiy 30.
Tel.: (371) 244-87-55, 244-87-20
[1] ![]() 1k 1−b
1k 1−b
3)
f x( ) = (7x−5)![]() , x0 =1; 4) f x( ) = (kx+b) , x0 =
, x0 =1; 4) f x( ) = (kx+b) , x0 = ![]() . k
. k
[2] ) f x( ) = sin 3 ,x A( ![]() ; ); 2) f x( ) =
cos5 ,x A(
; ); 2) f x( ) =
cos5 ,x A( ![]() ; );
; );
x π x 9
[3] ) f x( )
=
cos ![]() , A( ;
1 ); 4) f x( ) = sin
, A( ;
1 ); 4) f x( ) = sin ![]() , A(π;
, A(π; ).
[4] 2
[5] . f (x) funksiya uchun uning berilgan tenglamalar sistemasining yechimi (x0; y0) nuqtadan o‘tuvchi boshlang‘ich funksiyasini toping:
log x + log y = 3,
[6] .2. Fazoda vektorlar ustida amallar
Vektorlar ustida amallar. Vektorlarni qo‘shish, songa ko‘paytirish va skalar ko‘paytirish amallari xuddi tekislikdagidek aniqlanadi. a (a ; a ; a ) va b (b ; b ; b ) vektorlarning yig‘indisi deb a +b (a + b ; a + b ; a + b ) vektorga aytiladi (20-rasm).
bo‘yicha harakatlanayotgan bo‘lsin. Natijada yuk a+b vektor bo‘yicha harakatlanadi. Shuningdek, 20.c- rasmda tasvirlangan rus yozuvchisi Krilovning masali qahramonlari nima sababdan aravani joyidan qo‘zg‘ata olmayotganini sezgan bo‘lsangiz kerak.
[7] ) 300; 2) 2√3 +24; 3) 1513 l; 4) 64π cm3; 5) 35 dm2, 6,5 dm3.
Eslatma. Geometriyaga doir qiyinroq masalalar tartib raqami yulduzcha bilan, uyda bajarish tavsiya qilinayotgan masalalar qizil rangda berilgan.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.