
Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год
Дифференцирование показательной и логарифмической функций - Показательная и логарифмическая функции
Цель: привести формулы для производных показательной и логарифмической функций.
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Выведите формулу (где a, b > 0; а, b ≠ 1).
2. Известно, что lg 2 = а, lg 3 = b. Вычислите log412.
3.
Решите уравнение ![]()
Вариант 2
1.
Выведите формулу ![]() (где
а, b > 0; а ≠ 1, r ≠ 0).
(где
а, b > 0; а ≠ 1, r ≠ 0).
2. Известно, что lg 2 = a, lg 3 = b. Вычислите lg 18.
3.
Решите уравнение ![]()
III. Изучение нового материала
1. Число е. Функция у = ех, ее свойства, график, дифференцирование
Графики показательной функции изображались гладкими линиями, к которым в каждой точке можно провести касательную. Существование касательной к графику функции у = ах в точке х0означает ее дифференцируемость в этой точке. Поэтому показательная функция дифференцируема в каждой точке области определения.
Будем строить графики показательной функции у = ах для различных оснований а и касательные к ним в точке M(0; 1). Эти касательные образуют различные углы с осью абсцисс. В курсе математического анализа доказывается, что при определенном значении а е (2; 3) такая касательная образует угол 45° с осью ОХ. При этом угловой коэффициент такой касательной (или производная функции у = ах при х = 0) равен 1. Это число а обозначают буквой е. Доказано, что число е иррациональное (поэтому записывается в виде бесконечной десятичной непериодической дроби) и приближенно равно е ≈ 2,718... . Функцию у = ех называют экспонентой.
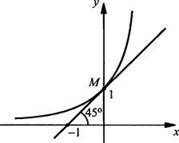
Итак,
существует такое число е (е ≈ 2,718), что показательная функция у = ех в
точке х = 0 имеет производную, равную 1, т. е. ![]() при
Δх → 0.
при
Δх → 0.
Сначала найдем формулу для производной экспоненты.
Теорема. Функция у = ех дифференцируема в каждой точке
области определения и (ех)' = ех. Докажем это. Найдем
приращение функции у = ех в точке х0. Получаем ![]()
![]() Вычислим
отношение приращения функции к приращению аргумента
Вычислим
отношение приращения функции к приращению аргумента ![]() при
Δх → 0. Тогда по определению производной получаем у' = ех или
(ех)' = ехпри любом х.
при
Δх → 0. Тогда по определению производной получаем у' = ех или
(ех)' = ехпри любом х.
Пример 1
Найдем
производную функции: ![]()
Данные функции являются сложными. Поэтому используем правило дифференцирования сложной функции и таблицу производных. Получаем:
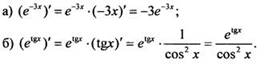
Пример 2
Построим
график функции ![]()
Область
определения этой функции - все действительные числа, т. е. х ∈ R. При х
≠ 0 функция принимает положительные значения у > 0, при х = 0 значение
функции у = 0. Найдем производную функции, используя правило дифференцирования
произведения функций: ![]() Так
как при всех значениях х величина ех > 0, то производная
обращается в 0 в двух точках: х = 0 и x = -2. Отметим эти точки на координатной
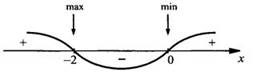
оси и проставим знаки производной в трех интервалах. Видно, что при х = -2
функция имеет максимум
Так
как при всех значениях х величина ех > 0, то производная
обращается в 0 в двух точках: х = 0 и x = -2. Отметим эти точки на координатной
оси и проставим знаки производной в трех интервалах. Видно, что при х = -2
функция имеет максимум ![]() при
х = 0 - минимум
при
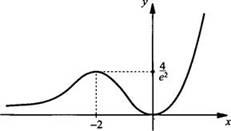
х = 0 - минимум ![]() Теперь
легко построить график данной функции.
Теперь
легко построить график данной функции.
Пример 3
При всех значениях параметра а определим число решений уравнения х2ех = а.
Воспользуемся
результатами предыдущей задачи. Для этого в одной системе координат надо
построить графики двух функций у1 = х2ех (уже
построен) и у2 = а (прямая, параллельная оси абсцисс). Тогда
очевидно, что при ![]() имеется
только одно решение, при
имеется
только одно решение, при ![]() существуют
три решения, а при
существуют
три решения, а при ![]() -
два решения.
-
два решения.
Пример 4
Напишем уравнение касательной, проведенной к графику функции f(х) = х2ех в точке с абсциссой х0 = -1.
Воспользуемся
результатами примера 2 и вычислим значение производной f(х) и самой функции
f(x) в точке х0 = -1. Получаем: ![]() и
и ![]() Подставим
эти величины в уравнение касательной
Подставим
эти величины в уравнение касательной ![]() Тогда
имеем:
Тогда
имеем: ![]() или
или ![]()
2. Натуральные логарифмы. Функция у = ln x, ее свойства, график, дифференцирование
При вычислениях часто используются логарифмы по основанию е. Так как число е положительно и не равно 1, то такие логарифмы определены. Напомним, что подобные логарифмы (по основанию е) называются натуральными и обозначаются символом ln, Т. е. ln x = logex.
Пример 5
Вычислим ![]() Сначала
преобразуем логарифмируемую величину, используя понятие рационального
показателя степени. Получаем
Сначала
преобразуем логарифмируемую величину, используя понятие рационального
показателя степени. Получаем 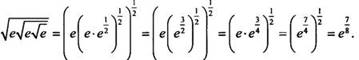 Теперь
легко вычислить и сам логарифм:
Теперь
легко вычислить и сам логарифм: ![]()
Прежде
всего покажем, что производная ![]() Используя
определение логарифма, запишем тождество х = еlnх и найдем
производную от обеих частей этого равенства:
Используя
определение логарифма, запишем тождество х = еlnх и найдем
производную от обеих частей этого равенства: ![]() или
или ![]() или
или ![]() откуда
откуда ![]()
Пример 6
Найдем
производную функции: ![]()
Приведенные функции являются сложными. Используя правило дифференцирования сложной функции, получим:
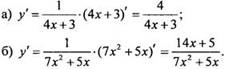
Производная логарифмической функции используется во многих прикладных задачах.
Пример 7
Исследуем функцию у = xln2 х и построим ее 1рафик.
Область
определения этой функции - множество положительных чисел. При всех х ≠ 1
значения функции положительны, при х = 1 функция у = 0. Найдем производную
данной функции: ![]()
![]() Производная
обращается в нуль в точках х = 1 и х = е2. Отметим эти точки на
координатной оси и расставим знаки производной в промежутках.
Производная
обращается в нуль в точках х = 1 и х = е2. Отметим эти точки на
координатной оси и расставим знаки производной в промежутках.
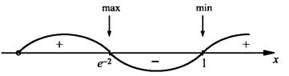
Видно,
что функция у(х) возрастает на промежутках (0; е-2] и [1; ∞) и
убывает на промежутке [е-2; 1]. В точке х = е-2 ≈
0,12 функция имеет максимум ![]() и
в точке х = 1 - минимум
и
в точке х = 1 - минимум ![]() Теперь
легко построить график функции у(х). На рисунке представлен эскиз графика (не
соблюден масштаб).
Теперь
легко построить график функции у(х). На рисунке представлен эскиз графика (не
соблюден масштаб).
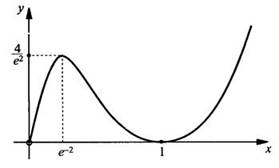
Пример 8
При различных значениях параметра а определим число решений уравнения xln2x = a.
В
одной системе координат построим графики функций y1 = xln2 х
(уже построен) и у2 = а (горизонтальная прямая). Тогда легко
ответить на вопрос задачи. При а ∈ (-∞;
0) уравнение решений не имеет (0 решений), при ![]() -
1 решение; при
-
1 решение; при ![]() -
три решения; при
-
три решения; при ![]() -
два решения.
-
два решения.
Пример 9
Напишем уравнение касательной, проведенной к графику функции f(х) = xln2 х в точке х0 = е.
Найдем
значение производной f’(x) и самой функции f(x) в точке х0 = е
и получим ![]() и
и ![]() (воспользовались
результатами примера 7). Подставим эти величины в уравнение касательной
(воспользовались
результатами примера 7). Подставим эти величины в уравнение касательной ![]() Имеем:
Имеем: ![]() Итак,
уравнение касательной у = 3х - 2е.
Итак,
уравнение касательной у = 3х - 2е.
Теперь
обобщим полученные формулы. Рассмотрим показательную функцию у = ax.
Запишем ее в виде ![]() и
найдем производную
и
найдем производную ![]() Итак,
Итак, ![]()
Рассмотрим
функцию у = logaх. Запишем ее в виде ![]() и
найдем производную:
и
найдем производную: ![]() Итак,
Итак, ![]()
Пример 10
Найдем
производную функции: ![]() .
.
Используя приведенные формулы, получим:
![]()
IV. Контрольные вопросы
1. Напишите формулы для нахождения производных функций у = ех и у = ах.
2. Приведите формулы для нахождения производных функций у= lnх и у = logax.
V. Задание на уроках
§ 47, № 1 (б); 2 (а, б); 4 (в); 6 (а); 8 (б); 10 (а, б); 13 (в, г); 16 (а, б); 17 (в, г); 19 (а); 20 (б); 24 (б); 27 (а); 28 (а, в).
VI. Задание на дом
§ 47, № 1 (г); 2 (в, г); 4 (г); 6 (в); 8 (г); 10 (в, г); 13 (а, б); 16 (в, г); 17 (а, б); 19 (б); 20 (а); 24 (в); 27 (б); 28 (б, г).
VII. Подведение итогов уроков
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.