алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Итоги контрольной работы - Урок 2 - Показательная и логарифмическая функции

Цели: сообщить результаты работы; рассмотреть наиболее типичные ошибки; разобрать трудные задачи.

Ход урока

I. Сообщение темы и целей урока

II. Итоги контрольной работы

III. Ответы и решения

Ответы

Вариант 1

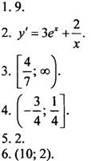
Вариант 2

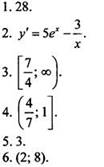
Вариант 3

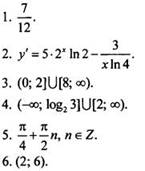
Вариант 4

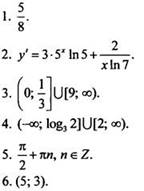
Решения

Вариант 5

1. Перейдем в log₂7 = b к основанию 10 и получим:  откуда  Теперь вычислим:  

Ответ: ab + 3a.

2. Учтем правило дифференцирования сложной функции и получим: 

Ответ: 

3. Область определения функции задается условием  Введем переменную t = 2^х > 0 и получим квадратное неравенство  Его решение t ∈ (0; 3] U [5; ∞). Вернемся к переменной х и учтем, что функция t = 2^х возрастающая. Получаем:  - область определения функции. Область значений функции E(f) = [0; ∞).

Ответ: 

4. Учтем, что sin x > 0, cos x > 0, и запишем неравенство в виде:  или  или tg x ≥ 2. С учетом ограничений запишем решение этого неравенства  где n ∈ Z.

Ответ:  где n ∈ Z.

5. Учтем, что  Тогда  Введем новую переменную  и получим рациональное уравнение  или  Его корни  Вернемся к старой переменной. Имеем два уравнения:  (его корень х = 2) и  (корень х = -2).

Ответ: 2; -2.

6. Запишем систему уравнений в виде  и введем новые переменные  Получаем систему уравнений  Решения этой системы а = 1, b = 4 и а = 4, b = 1. Вернемся к старым переменным. Имеем две системы уравнений:

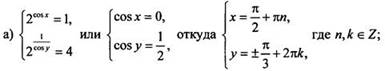
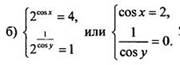 Эта система решений не имеет.

Ответ: 

Вариант 6

1. Найдем  Перейдем в log₃₀8 к основанию 10 и получим: 

Ответ: 

2. Учтем правило дифференцирования сложной функции и получим: 

Ответ: 

3. Область определения функции задается условием  Введем переменную t = 3^х > 0 и получим квадратное неравенство  Решение этого неравенства t ∈ (0; 4] U [5; ∞). Вернемся к переменной х и учтем, что функция t = 3^х возрастающая. Получаем  - область определения функции. Область значений функции E(f) = [0; ∞).

Ответ: 

4. Учтем, что sinx > 0, cosx > 0, и запишем неравенство в виде:  или  или  С учетом ограничений запишем решение этого неравенства  где n ∈ Z.

5. Учтем, что  Тогда  Введем новую переменную  и получим рациональное уравнение  или t² – 14t + 1 = 0. Его корни t_1,2 = 7 ± √48 > 0. Вернемся к старой переменной. Имеем два уравнения:  (его корень х = 2) и  (корень х = -2).

Ответ: 2; -2.

6. Запишем систему уравнений в виде  и введем новые переменные  Получаем систему уравнений  Решения этой системы a = 3, b = 1 и а = -1, b = -3 (не подходит, т. к. а, b > 0). Вернемся к старым переменным. Имеем систему уравнений  или 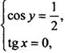 откуда  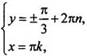где n, k ∈ Z.

Ответ:  где n, k ∈ Z.