алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Вычисление площадей плоских фигур с помощью определенного интеграла - Определенный интеграл - Первообразная и интеграл

Цель: отработать навыки вычисления площадей фигур.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Задача о площади криволинейной трапеции.

2. Вычислите определенный интеграл:

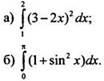
Вариант 2

1. Задача о перемещении точки.

2. Вычислите определенный интеграл:

III. Изучение нового материала

Так как понятие определенного интеграла в первую очередь связано с вычислением площади криволинейной трапеции, то остановимся подробнее на нахождении площадей плоских фигур. Условно можно выделить несколько характерных типов таких задач.

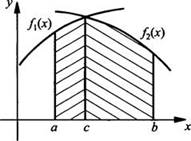
1. Площадь фигуры, ограниченной графиками функций f₁(x) и f₂(х) при условии f₁(x) ≥ f₂(х).

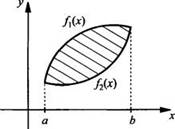
Пусть графики функций f₁(x) и f₂(х) пересекаются в точках х = a и х = b и на отрезке [а; b] выполнено неравенство f₁(x) ≥ f₂(х). Тогда площадь заштрихованной фигуры, ограниченной графиками данных функций, равна 

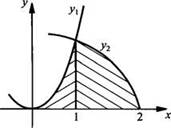
Пример 1

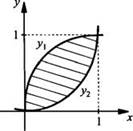
Найдем площадь фигуры, ограниченной линиями у₁ = √х и у₂ = x².

Построим графики данных функций у₁ = √х и у₂ = x² и найдем точки пересечения этих графиков. Получаем уравнение: √х = х², или х = х⁴ или 0 = х(х³ - 1). Корни этого уравнения х₁ = 0 и х₂= 1. На промежутке [0; 1] выполнено неравенство y₁ ≥ у₂. Тогда площадь заштрихованной фигуры равна 

2. Площадь фигуры, ограниченной графиками функций f₁(x) и f₂(x) на отрезке [а; b].

Пусть графики функций f₁(x) и f₂(х) пересекаются в точке с ∈ [a; b]. Тогда верхняя граница криволинейной трапеции представляет собой две различные линии f₁(x) и f₂(х). Поэтому площадь заштрихованной фигуры равна 

Пример 2

Найдем площадь фигуры, ограниченной линиями  и расположенной в первой четверти.

Построим графики функций  и найдем точку пересечения. Получаем уравнение:  или х⁴ = 2 - х, или (х - 1)(х³ + х² + х + 2) = 0. Очевидно, что такое уравнение при х ≥ 0 имеет только один корень х = 1. Тогда площадь заштрихованной фигуры равна 

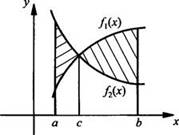
3. Площадь фигуры, ограниченной графиками функций f₁(x) и f₂(х) различной величины на отрезке [а; b].

Фактически этот тип задач - сочетание двух предыдущих разновидностей. Найдем площадь криволинейной трапеции, ограниченной линиями f₁(x) и f₂(х) и прямыми х = а и х = b. Пусть графики функций f₁(x) и f₂(х) пересекаются в точке с ∈ [a; b]. Тогда площадь заштрихованной фигуры равна 

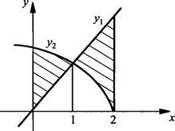
Пример 3

Найдём площадь фигуры, ограниченной линиями 

Нарисуем заданную фигуру и найдем точку пересечения графиков функций у₁ и у₂. Получаем уравнение:  или х² + х - 2 = 0. На промежутке [0; 2] это уравнение имеет единственный корень х = 1. Найдем площадь заштрихованной фигуры: 

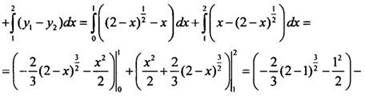
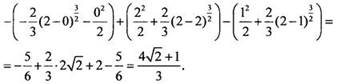
4. Прочие типы задач

К этой разновидности отнесем задачи с несколько нестандартными условиями. Несмотря на это, подобные задачи решаются теми же способами. Может быть, понадобится более широкое привлечение дополнительных сведений.

Пример 4

Найдем площадь фигуры, ограниченной графиком функции f(x) = х² + 10 и касательными к этому графику, проведенными из точки A(0; 1).

Построим заданную фигуру. Очевидно, что такая фигура симметрична относительно оси ординат. Поэтому достаточно найти сначала площадь половины этой фигуры. Прежде всего получим уравнение касательной. Пусть касание происходит в точке x₀. Найдем производную f’(x) = 2х и значения функции и производной в точке x₀ и получим:  Запишем уравнение касательной:  или  Так как касательная проходит через точку A(0; 1), то получаем уравнение  откуда х₀ = ±3. Тогда уравнение касательных у = ±6х + 1. Найдем площадь заданной фигуры: 

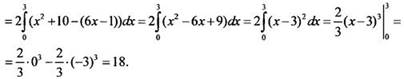
Пример 5

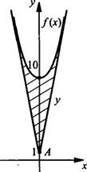
Фигура ограничена графиком функции f(x) = (х + 3)² и прямыми x = 0 и у = 0. Под какими углами к оси абсцисс надо провести две прямые через точку А(0; 9), чтобы они разбили фигуру на три равновеликие части?

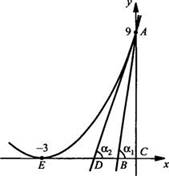
Сначала найдем площадь криволинейной трапеции АСЕ и получим:  Значит, каждая равновеликая часть фигуры будет иметь площадь 3. Тогда  откуда  Найдем: 

Площадь  поэтому  откуда  Теперь найдем: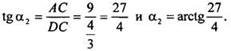 

Пример 6

Найдем наименьшее значение площади фигуры, ограниченной параболой у₁ = х² + 2х - 3 и прямой у₂ = ax +1. При каком значении параметра а оно достигается?

Пусть графики данных функций пересекаются в точках х₁ и х₂ (x₁ < х₂). При всех х ∈ [х₁; х₂] выполнено неравенство у₁ ≤ у₂. Тогда площадь заданной фигуры 

Точки пересечения х₁ и х₂ являются корнями уравнения х² + 2х - 3 = ах + 1 или х² + (2 - а)х - 4 = 0 и равны  Понятно, что подставить такие пределы интегрирования в выражение для площади S нереально. Поэтому воспользуемся формулами Виета: х₁ + х₂ = а - 2 и x₁x₂ = -4. Найдем необходимые для вычисления комбинации корней: 

Теперь преобразуем выражение для площади S к более удобному виду: 

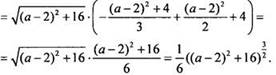 Очевидно, что наименьшее значение площадь S принимает при а = 2 и оно равно 

Заметим, что применение определенных интегралов намного разнообразнее. В математике они могут быть использованы для вычисления объемов тел (пирамида, конус и т. д.), в том числе и объемов тел вращения; длин дуг кривых; площадей поверхностей тел вращения и т. д. В физике определенные интегралы используются для вычисления работы переменной силы, центра масс, энергии тела и т. д.

IV. Задание на уроках

§ 49, № 11 (б); 14 (а, б); 17 (б); 19 (а, б); 23 (в, г); 25 (а); 26 (в, г); 27 (а); 28 (б); 29 (а); 31 (а); 32 (в, г); 33 (а); 34 (б).

V. Задание на дом

§ 49, № 11 (г); 14 (в, г); 17 (а); 19 (в, г); 23 (а, б); 25 (б); 26 (а, б); 27 (б); 28 (а); 29 (б); 31 (б); 32 (а, б); 33 (б); 34 (а).

VI. Творческие задания

1. При каких значениях параметра а выполнено условие:

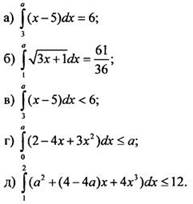
Ответы: а) 1 и 9; б) 7/4; в) (1; 9); г) (-∞; 0] U {1}; д) 3. 4

2. Вычислите площадь фигуры, ограниченной линиями:

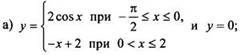
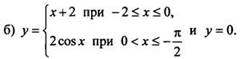
Ответы: а, б) 4.

3. Найдите площадь фигуры, заданной неравенством:

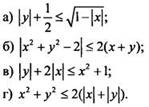
Ответы: а) 5/6; б) 2π + 4; в) 4/3; г) 4π + 8.

4. Найдите площадь фигуры, ограниченной кривой у = х² + х + 1, касательной к ней, проведенной в точке A(1; 3), и прямой х = -1.

Ответ: 7/6.

5. Вычислите площадь фигуры, ограниченной параболой у = х² - 2х + 2, касательной к ней в точке A(3; 5) и осью ординат.

Ответ: 9.

6. Найдите площадь фигуры, ограниченной кривой  и прямой, проходящей через точки А(2; 2) и B(4; 3).

Ответ: 2/3.

7. Найдите площадь фигуры, ограниченной кривой  и прямой, проходящей через точки A(1; 1) и B(-5; 3).

Ответ: 1/6.

8. Вычислите интеграл, используя его геометрический смысл:

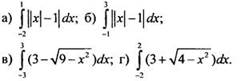
Ответы: а) 3/2; б) 3; в) 18 - 4,5π; г) 12 + 2π.

VII. Подведение итогов уроков