алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Равносильность уравнений - Уравнения и неравенства. Системы уравнений и неравенств

Цель: рассмотреть понятие равносильности уравнений и равносильные преобразования уравнений.

Ход уроков

I. Сообщение темы и цели уроков

II. Изучение нового материала

Разумеется, рассматриваемый материал не является новым: начиная с 7 класса изучались различные типы уравнений и неравенств с одной переменной, системы неравенств с одной переменной, системы уравнений с двумя переменными. Столь огромный интерес к решению уравнений и неравенств вполне оправдан: именно эти объекты чаще всего являются математическими моделями реальных ситуаций в повседневной жизни, науки и технике. В завершение обучения еще раз обратимся к уравнениям и неравенствам, чтобы рассмотреть их с самых общих позиций.

Необходимо обсудить принципиальные вопросы, связанные с решением уравнений с одной переменной: равносильные уравнения и равносильные преобразования уравнений, посторонние корни и потеря корней в уравнениях и т. д.

Определение 1. Два уравнения с одной переменной f(x) = g(x) и р(х) = h(x) называют равносильными, если множества их решений совпадают. Другими словами, два уравнения будут равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.

Пример 1

а) Уравнения х - 3 = 0 и log₃x = 1 равносильны, т. к. оба имеют единственный корень х = 3.

б) Уравнения х² + 1 = 0 и lg(|x| + 4) = 0 равносильны, т. к. каждое из них корней не имеет.

Определение 2. Если каждый корень уравнения f(х) = g(x) (1) является корнем уравнения р(х) = h(x) (2), то уравнение (2) называют следствием уравнения (1).

Пример 2

а) Уравнение х - 3 = 0 имеет единственный корень х = 3, который является также корнем уравнения х² - 5х + 6 = 0 (второй корень этого квадратного уравнения х = 2). Поэтому уравнение х² - 5х + 6 = 0 является следствием уравнения х - 3 = 0.

б) Уравнение х² - 4х + 3 = 0 имеет корни х₁ = 3 и x₂ = 1, уравнение х² - 5х + 6 = 0 имеет корни x₃ = 3 и х₄ = 2 (т. е. оба уравнения имеют только один общий корень х = 3). Поэтому ни одно из уравнений не является следствием другого.

Очевидно, что два уравнения равносильны тогда и только тогда, когда каждое из них является следствием другого.

При решении любых уравнений используется стандартная схема: с помощью преобразований исходное уравнение заменяется более простым (как правило, линейным или квадратным), которое затем решают.

Пример 3

Показательное уравнение  заменяем иррациональным уравнением  После возведения в квадрат обеих частей уравнения получаем квадратное уравнение: 3х - 2 = (2х - 1)²или 0 = 4х² - 7х + 3. Корни этого уравнения x₁ = 1 и х₂ = 3/4 являются также корнями исходного показательного уравнения.

Разумеется, идеальными являются такие преобразования, которые приводят к равносильным уравнениям. В этом случае окончательное уравнение имеет те же корни, что и исходное. Если преобразования приводят к уравнениям-следствиям, то полученное уравнение может иметь и те корни, которые не имеет исходное уравнение (посторонние корни). Но все корни исходного уравнения сохраняются, т. е. потери корней не происходит (могут лишь появиться посторонние корни).

В идеале решение уравнения осуществляется в три этапа.

Первый этап - технический. Проводится цепочка преобразований от исходного до самого простого, которое затем решают.

Второй этап - анализ решений. Анализируются выполненные преобразования. Выясняют, все ли такие преобразования являются равносильными.

Третий этап - проверка. Если некоторые преобразования могут привести к уравнению-следствию, то обязательна проверка всех найденных корней их подстановкой в исходное уравнение.

В связи с изложенной схемой решения уравнения возникают по крайней мере четыре основных вопроса.

1. Какие преобразования приводят к равносильному уравнению?

2. Какие преобразования могут привести к уравнению-следствию?

3. Если в цепочке преобразований было получено уравнение- следствие и найдены его корни, то как их проверить в случае, когда непосредственная проверка приводит к значительным трудностям?

4. В каких случаях преобразования могут привести к потере корней исходного уравнения и как этого избежать?

Последовательно ответим на эти вопросы.

1. Теоремы о равносильности уравнений

В основном при решении уравнений используются шесть теорем равносильности. Первые три теоремы безусловные. Они гарантируют равносильность преобразований без дополнительных условий. Их применение обычно происходит автоматически, без особых размышлений.

Теорема 1. Если любой член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному. Например, уравнения  и  равносильны.

Теорема 2. Если обе части уравнения возвести в одну и ту же нечетную степень, то получится уравнение, равносильное данному. Например, уравнения  и 3x + 2 = x³ равносильны.

Теорема 3. Показательное уравнение  (где a > 0, а ≠ 1) равносильно уравнению f(x) = g(x). Например, показательное уравнение  равносильно иррациональному уравнению 

Следующие три теоремы условные. Они справедливы лишь при выполнении определенных условий. При их применении потребуются некоторая внимательность и аккуратность.

Сначала напомним понятие, важное для определенных типов уравнений.

Определение 3. Областью определения уравнения f(x) = g(x) (или областью допустимых значений (ОДЗ) переменной такого уравнения) называют множество тех значений переменной х, при которых имеют смысл выражения f(x) и g(x).

Теорема 4. Если обе части уравнения f(x) = g(x) умножить на одно и то же выражение h(x), которое:

а) имеет смысл в области определения уравнения f(x) = g(x);

б) нигде в этой области не обращается в нуль, то получится уравнение f(x)h(x) = g(x)h(x), равносильное данному.

Пример 4

ОДЗ уравнения  задается условиями 2х + 1 ≥ 0 и х + 2 ≠ 0, что дает х ≥ -0,5. Выражение h(x) = x + 2 b этой области имеет смысл и нигде не обращается в нуль. Поэтому уравнение f(x)h(х) = g(x)h(x) равносильно уравнению f(x) = g(х), т. е. уравнение  равносильно уравнению  (после умножения на выражение h(x) = х + 2).

Теорема 5. Если обе части уравнения f(x) = g(x) неотрицательны в области определения уравнения, то после возведения обеих его частей в одну и ту же четную степень п получится уравнение, равносильное данному: 

Пример 5

ОДЗ иррационального уравнения  задается неравенством 3х - 2 ≥ 0, решение которого х ≥ 2/3.

В этой ОДЗ обе части уравнения неотрицательны. Возведем в квадрат обе части уравнения и получим равносильное квадратное уравнение: 3х - 2 = (2х - 1)² или 0 = 4х² - 7х + 3. Корни x₁ = 1 и х₂= 3/4 также будут корнями исходного уравнения.

Теорема 6. Если f(х) > 0 и g(x) > 0, то логарифмическое уравнение  (где a > 0, а ≠ 1) равносильно уравнению f(x) = g(x).

Пример 6

В логарифмическом уравнении  функции f(x) = Зх² + 2 и g(x) = 4|х| + 1 принимают положительные значения при всех значениях переменной х. Поэтому данное уравнение равносильно уравнению 3х + 2 = 4|х| + 1. Корни х_1,2 = 1 и х_3,4 = ±1/3 этого уравнения являются также корнями исходного уравнения.

2. Преобразование данного уравнения в уравнение-следствие

Если нарушаются условия применимости теорем 4—6, то получится уравнение-следствие. Рассмотрим соответствующие примеры.

Пример 7

а) Уравнение х - 2 = 1 имеет единственный корень х = 3. Умножим обе части данного уравнения на выражение х - 4 и получим квадратное уравнение: (х - 2)(х - 4) = х - 4 или х² - 7х + 12 = 0, которое имеет два корня: x₁ = 3 и х₂ = 4. Корень х = 4 является посторонним для уравнения х - 2 = 1. Это связано с тем, что обе части исходного уравнения были умножены на выражение х - 4, которое обращается в нуль при х = 4 (нарушены условия теоремы 4). Именно это значение оказалось посторонним корнем. Поэтому уравнение х² - 7х + 12 = 0 является следствием уравнения х – 2 = 1.

б) Рассмотрим то же самое уравнение х - 2 = 1 и возведем обе его части в квадрат. Получим квадратное уравнение: (х - 2)² = 1 или х² - 4х + 3 = 0. Оно имеет два корня: x₁ = 3 и х₂ = 1. Второй корень х = 1 является посторонним для уравнения х - 2 = 1. Это связано с тем, что обе части исходного уравнения были возведены в квадрат (четная степень). При этом левая часть х - 2 может быть и отрицательной (нарушены условия теоремы 5). Поэтому уравнение х² - 4х + 3 = 0 - следствие уравнения х – 2 = 1.

в) Обсудим уравнение Iog₇(х² + 5х) = log₇2х + 4. Потенциируя, получим уравнение: х² + 5х = 2х + 4 или х² + 3х - 4 = 0, корни которого x₁ = 1 и x₂ = -4. Второй корень х = -4 является посторонним для логарифмического уравнения, т. к. выражения х² + 5х и 2х + 4 принимают отрицательные значения. Появление постороннего корня связано с нарушением условий теоремы 6. Поэтому уравнение х² + 3х - 4 = 0 - следствие уравнения log₇(х² + 5х) = log₇2х + 4.

К появлению посторонних корней может привести расширение области определения уравнения. Возможные причины расширения ОДЗ:

1) избавление от знаменателей, содержащих переменную величину;

2) избавление от корней четной степени;

3) избавление от знаков логарифмов.

Пример 8

Решим уравнение:

 ОДЗ этого уравнения - любые значения х, кроме х = 2. Умножим обе части уравнения на выражение х - 2. Получим квадратное уравнение: х² - 4х = х - 6 или х² - 5х + 6 = 0. ОДЗ такого уравнения - любые действительные значения х. При этом область определения уравнения расширилась. Корни квадратного уравнения: x₁ = 3 и х₂ = 2. При этом корень х = 2 в ОДЗ исходного уравнения не входит и не является его решением. Итак, данное уравнение имеет единственный корень х = 3;

 ОДЗ такого уравнения задается системой неравенств  решение которой х ≥ 3. Возведем в квадрат (четная степень) обе части данного иррационального уравнения. Получим квадратное уравнение: х² - 3х = 2x - 6 или х² - 5х + 6 = 0. ОДЗ этого уравнения - любые действительные значения х. Видно, что область определения уравнения расширилась. Корни квадратного уравнения: х₁ = 3 и x₂ = 2. Второй корень в ОДЗ исходного уравнения не входит и не является его решением. Поэтому данное уравнение имеет только корень x = 3;

в) log₇(x² - 2х) = log₇(3x - 6). ОДЗ этого уравнения определяется системой неравенств  решение которой х > 2. Потенциируя, получим квадратное уравнение: х² - 2х = 3х - 6 или х² - 5х + 6 = 0. ОДЗ такого уравнения - любые действительные значения х. Область определения уравнения расширилась. Корни квадратного уравнения: x₁ = 3 и х₂ = 2. При этом корень x = 2 в ОДЗ данного уравнения не входит и является посторонним.

На примере рассмотрим этапы решения уравнения.

Пример 9

Решим уравнение 

Первый этап - технический. Выполним цепочку преобразований, получим наиболее простое уравнение и решим его.

Уединим один из корней в левой части и запишем уравнение в виде:  Возведем в квадрат обе части уравнения:  или  или  Опять уединим в левой части корень и получим:  или  Возведем обе части уравнения в квадрат: 16(3x - 2) = (10 - x)² или 0 = x² – 68x + 132. Корни этого квадратного уравнения х₁ = 2 и x₂ = 66.

Второй этап - анализ решения. Проверим выполненные преобразования на равносильность. Два раза части уравнения возводились в квадрат, что не является равносильным преобразованием. Поэтому проверка корней обязательна.

Третий этап — проверка. Подставим найденные корни в исходное уравнение.

При x = 2 получаем:  или 2 + 4 = 6 - верное равенство.

При x = 66 имеем:  - явно неверное равенство, т. к. уже первое слагаемое в левой части равно 14 и второе слагаемое положительно. Поэтому x = 66 - посторонний корень. Итак, данное уравнение имеет единственный корень x = 2.

Заметим, что корень х = 66 можно было проверить и проще. На некотором этапе преобразований было получено уравнение  Левая часть его неотрицательна. Поэтому правая часть также должна быть неотрицательной, т. е. 10 - х ≥ 0, откуда х ≤ 10. Тогда корень x = 66 будет посторонним.

3. O проверке корней

Очень часто при проверке корней уравнения используют ОДЗ.

Пример 10

Решим уравнение 

Первый этап. Запишем уравнение в виде  Используя формулу для суммы логарифмов, получим:  или  По определению логарифма имеем квадратное уравнение: 2х² + 11х + 15 = 1 или 2х² + 11х + 14 = 0. Корни этого уравнения: х₁ = -2 и х₂ = -3,5.

Второй этап. При использовании формулы для суммы логарифмов происходит расширение области определения уравнения. Поэтому проверка корней обязательна.

Третий этап. Так как неравносильные преобразования не применялись, то проверка корней может быть выполнена по ОДЗ исходного уравнения. Эта область определяется системой неравенств  Корень x₁ = -2 этой системе удовлетворяет, а корень х₂ = -3,5 не удовлетворяет уже первому неравенству. Поэтому этот корень посторонний. Итак, данное уравнение имеет единственный корень х = -2.

Заметим, что в повседневной жизни при решении уравнений обычно явно не выделяют три этапа. Хотя все эти три этапа решения в той или иной форме выполняют.

Пример 11

Решим уравнение 

Запишем уравнение в виде  и используем формулу для разности логарифмов. Получим:  или  Потенциируя, придем к тригонометрическому уравнению tgx = √3. Его решения  (где n ∈ Z ). Однако надо учесть ОДЗ уравнения, которая определяется системой неравенств 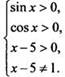 Первые два неравенства означают, что угол х располагается в первой координатной четверти. Поэтому n должно быть числом четным, т. е. n = 2k (где k ∈ Z). Тогда найденное решение имеет вид  (где k ∈ Z ). Из третьего неравенства получаем х > 5. Наши решения попадают в этот промежуток только при k = 1, 2, 3, т. е. при k ∈ N. Четвертое неравенство выполняется всегда, т. к. π - число иррациональное и х ≠ 6 при любом натуральном значении k. Итак, данное логарифмическое уравнение имеет решения  где k ∈ N.

В данном примере все три этапа решения были проведены параллельно и взаимосвязанно.

Разумеется, проверка решения по ОДЗ не является единственной и не всегда дает результат. Например, в примере 9, помимо расширения ОДЗ уравнения, имели место неравносильные преобразования. Поэтому, хотя оба значения x₁ = 2 и х₂ = 66 находились в ОДЗ данного уравнения, корень х = 66 оказался посторонним. Для подобных случаев рекомендуем проверять решения подстановкой или использовать другие соображения.

4. О потере корней

В предыдущем разделе обсуждался вопрос о появлении посторонних корней. Эти корни могут быть обнаружены путем их проверки (например, подстановкой). Гораздо хуже, если в ходе преобразований происходит потеря корней уравнения.

Укажем две причины потери корней при решении уравнений:

1) деление обеих частей уравнения на одно и то же выражение h(x) (кроме тех случаев, когда точно известно, что всюду в области определения уравнения выражение h(x) ≠ 0);

2) сужение ОДЗ в процессе решения уравнения.

В первом случае обычно используют разложение уравнения на множители, т. е. уравнение f(x)h(x) = g(x)h(x) записывают в виде g(x)[f(x) - g(x)] = 0. Далее такое уравнение распадается на два: а) h(x) = 0; б) f(x) - g(x) = 0.

Пример 12

Решим уравнение 

Перенесем все члены уравнения в левую часть и вынесем общий множитель 2х - 1 за скобки. Получаем: (2х - 1)(х² + 3 - 4х) = 0. Если произведение множителей равно нулю, то один из них равен нулю, а остальные не теряют смысла. Получаем два уравнения:

а) линейное уравнение 2х - 1 = 0 и его корень x₁ = 0,5;

б) квадратное уравнение х² - 4х + 3 = 0 и его корни х₂ = 1 и х₃ = 3. Таким образом, данное уравнение имеет три корня: х₁ = 0,5, х₂ = 1, х₃ = 3.

Во втором случае необходимо грамотно применять имеющиеся формулы.

Пример 13

Решим уравнение 

Используем формулу для логарифма частного и получим  Запишем уравнение в виде log₃(2x + 3) = log₃(x - 1). Потенциируя, получим линейное уравнение 2х + 3 = х - 1, корень которого х = -4. Легко проверить, что для такого значения х выражения 2х + 3 и х - 1 отрицательны. Поэтому х = -4 не является корнем уравнения log₃(2x + 3) = log₃(x - 1). Тем не менее х = -4 является корнем исходного уравнения. Это связано с тем, что в ходе преобразований была сужена ОДЗ уравнения. Действительно, ОДЗ исходного уравнения определяется неравенством  и х ∈ (-∞; -1,5) U (1; ∞). ОДЗ преобразованного уравнения log₃(2х + 3) = log₃(х - 1) определяется системой неравенств  решение которой х ∈ (1; ∞). Таким образом, ОДЗ исходного уравнения была сужена на промежуток (-∞; -1,5), в который и попал корень х = -4.

Разумеется, данное уравнение  надо решать по-другому. Используя определение логарифма, сразу получаем рациональное уравнение  Затем приходим к линейному уравнению 2х + 3 = х - 1 и находим единственный корень этого и исходного уравнений х = -4.

Пример 14

Решим уравнение 

Так как основания логарифмов разные, то перейдем к основанию х. Используем формулу для логарифма произведения и получим:  или  или  Введем новую переменную a = log_x2. Имеем paциональное уравнение:  или  или -2 = 3a, откуда a = -2/3. Вернемся к старой переменной. Получаем уравнение:  По определению логарифма имеем:  Возведем обе части этого равенства в степень (-3/2) и найдем  Проверка показывает, что это корень исходного уравнения. Вместе с тем легко проверить, что х = 1 также корень исходного уравнения. Он был потерян при переходе к логарифмам с основанием х (х ≠ 1). При этом произошло сужение ОДЗ уравнения.

Разумнее было бы в исходном уравнении переходить к логарифмам с известным основанием, например с основанием 2. Получаем:  или  или  Введем новую переменную b = log₂x. Имеем рациональное уравнение:  или   или 0 = 2b² + 3b, или  Корни этого уравнения b₁ = 0 и b₂ = -3/2. Вернемся к старой переменной. Получаем два уравнения: log₂x = 0 (корень х₁ = 2⁰ = 1) и  (корень ). Итак, данное уравнение имеет два корня: х₁ = 1 и .

III. Контрольные вопросы

1. Понятие равносильных уравнений.

2. Определение уравнения-следствия.

3. Три этапа решения уравнения.

4. Теоремы о равносильности уравнений (фронтальный опрос).

5. Преобразование данного уравнения в уравнение-следствие.

6. Расширение области определения уравнения.

7. Причины потери корней при решении уравнений.

IV. Задание на уроках

§ 55, № 1; 3 (а, б); 4; 6 (а); 7 (б); 8 (а); 9 (б, в); 10 (а, б); 11 (а); 12 (б, г).

V. Задание на дом

§ 55, № 2; 3 (в, г); 5; 6 (б); 7 (а); 8 (б); 9 (а, г); 10 (в, г); 11 (б); 12 (а, в).

VI. Подведение итогов уроков