алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Понятие корня n-й степени из действительного числа - Степени и корни. Степенные функции

Цель: рассмотреть корень n-й степени из числа.

Ход уроков

I. Сообщение темы и цели уроков

II. Изучение нового материала

Сначала необходимо обсудить с учащимися понятие квадратного корня из числа а: это такое число, квадрат которого равен числу а. Другими словами, х - квадратный корень из числа а, если выполнено равенство х² = а.

Предложите ученикам по аналогии ввести понятие корня n-й степени из числа а. Обобщение совершенно очевидно: корнем n-й степени из числа а называется такое число х, n-я степень которого равна а. Другими словами, х - решение уравнения хⁿ = а.

Пример 1

а) Число 4 является корнем уравнения х³ = 64, т. к. выполнено равенство 4³ = 64.

б) Числа 2 и -2 являются корнями уравнения х⁴ = 16, т. к. выполнены равенства: 2⁴ = 16 и (-2)⁴ = 16.

Вообще, при рассмотрении уравнения хⁿ = а, как правило, получаем решения, которые являются иррациональными числами. Такое решение обозначают символом  (читают: корень n-й степени из числа а). Например, решением уравнения х³ = 2 является иррациональное число, которое обозначают символом 

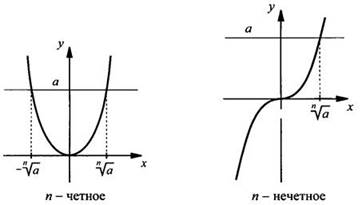
При решении уравнения хⁿ = а (где а > 0, n ∈ N, n ≥ 2) получаем в случае четного n два корня:  в случае нечетного n - один корень  Это проиллюстрировано рисунком, на котором приведен график функции у = хⁿ и приведено решение уравнения хⁿ = а.

Приведем теперь строгое определение корня.

Определение 1. Корнем n-й степени (n = 2, 3, 4, 5, ...) из неотрицательного числа а называют такое неотрицательное число, при возведении которого в степень получают число а. Таким образом, если a ≥ 0 и n = 2, 3, 4, 5, то: 1)  и 2)  Приняты термины:  - корень n-й степени из числа а, число а - подкоренное число, число n - показатель корня.

Для наиболее часто встречающихся корней приняты специальные названия: при n = 2 говорят “квадратный корень” и обозначают символом √a, при n = 3 говорят “кубический корень” и обозначают символом 

Вообще, зависимости  обозначают одну и ту же связь между неотрицательными числами а и b. Операцию нахождения корня называют извлечением корня. Такая операция является обратной по отношению к операции возведения в соответствующую степень, что видно из данных таблицы.

Пример 2

Используя определение, вычислим:

а)  так как 125 ≥ 0, 5 ≥ 0 и 5³ = 125;

б)  так как 0,0081 ≥ 0, 0,3 ≥ 0 и 0,3⁴ = 0,0081;

в)  так как 

г)  так как 

д)  так как 0 ≥ 0 и 0⁹ = 0.

Операцию извлечения корня можно ввести и для отрицательного числа а, но только в случае нечетного показателяn корня. Например, равенство (-4)³ = -64 можно записать в виде  Для этого случая определение корня аналогично уже приведенному.

Определение 2. Корнем нечетной степени n (n = 3, 5, 7, ...) из отрицательного числа а называют такое отрицательное число, при возведении которого в степень n получают число а. Таким образом, если а < 0 и n = 3, 5, 7,..., то: 1)  и 2) 

Пример 3

Используя определение, вычислим:

а)  так как -32 < 0, -2 < 0 и (-2)⁵ = -32;

б)  так как -0,125 < 0, -0,5 < 0 и (-0,5)³ = -0,125;

в)  так как 

Таким образом, корень четной степени имеет смысл (т. е. определен) только для неотрицательных подкоренных чисел; корень нечетной степени имеет смысл для любых подкоренных чисел.

В заключение остановимся на решении простейших иррациональных уравнений и неравенств.

Пример 4

Решим уравнение:

а)  Корень четной степени - число неотрицательное и не может равняться числу -1. Поэтому данное уравнение решений не имеет.

б)  Обе части уравнения - неотрицательные выражение и число. Поэтому обе части возведем в четвертую степень и получим линейное уравнение 5х - 14 = 1 или 5х = 15, корень которого х = 3. Итак, данное иррациональное уравнение имеет единственное решение х = 3.

в)  Уравнение содержит корень нечетной степени. Возведем в куб обе части и получим линейное уравнение 3х + 10 = -8 или 3х = -18, корень которого х = -6. Таким образом, данное уравнение имеет единственное решение х = -6.

г)  Левая часть уравнения - неотрицательное выражение, т. к. является квадратным корнем. Поэтому правая часть также должна быть неотрицательным выражением, т. е. х + 1 ≥ 0 (откуда х ≥ -1). Возведем в квадрат обе части данного уравнения 11 - х = (х + 1)². При этом очевидно, что подкоренное выражение 11 - х ≥ 0, т. к. (х + 1)² ≥ 0. Получим квадратное уравнение 11 - х = х² + 2х + 1 или 0 = х² + 3х - 10. Его корни x₁ = 2 и х₂ = -5. Однако условию х ≥ -1 удовлетворяет только значение х = 2. Поэтому корень х = -5 посторонний. Итак, данное иррациональное уравнение имеет единственное решение х = 2.

Пример 5

Решим неравенство:

а)  Левая часть неравенства - неотрицательное выражение, правая часть - отрицательное число. Поэтому неравенство выполнено для всех значений х из ОДЗ неравенства. Решим неравенство  например, методом интервалов. Получаем х ∈ [1,5; 4). Этот промежуток является решением данного иррационального неравенства.

б)  Левая часть неравенства - неотрицательное выражение, правая часть - положительное число. Поэтому возведем обе части неравенства в квадрат: х² + 3х ≥ 4. При этом подкоренное выражение положительно. Решим полученное квадратное неравенство х³ + 3х - 4 ≥ 0 и получим: х ∈ (-∞; -4] U [1; +∞).

в)  ОДЗ неравенства задается условием х² + 8х ≥ 0. Решение этого неравенства х ∈ (-∞; -8] U [0; +∞). Обе неотрицательные части неравенства  возведем в квадрат. Получаем квадратное неравенство х² + 8х < 9 или х² + 8х - 9 < 0. Его решение х ∈ (-9; 1). С учетом ОДЗ находим решение данного иррационального неравенства: х ∈ (-9; -8] U [0; 1).

г)  ОДЗ неравенства определяется условием х + 3 ≥ 0, откуда х ∈ [-3; +∞). При таких значениях х правая часть данного неравенства может быть и отрицательной, и положительной.

Рассмотрим эти случаи.

1) При 3 - x < 0 (т. е. х > 3) правая часть отрицательна, левая - неотрицательна. Получаем верное неравенство. Поэтому промежуток х ∈ (3; +∞) - решение данного неравенства.

2) При 3 - х ≥ 0 (т. е. х < 3) обе части неравенства неотрицательны. Возведем их в квадрат. Получаем: х + 3 > (3 - х)² или 0 > х² - 7х + 6. Решение этого квадратного неравенства - промежуток х ∈ (1; 6). С учетом ограничения х ≤ 3 находим, что промежуток х ∈ (1; 3] - решение данного неравенства.

Объединяя решения рассмотренных двух случаев, окончательно найдем решение данного иррационального неравенства: х ∈ (1; +∞).

III. Контрольные вопросы

1. Определение корня я-й степени из неотрицательного числа.

2. Корень нечетной степени из отрицательного числа.

IV. Задание на уроках

§ 33 № 1 (а, б); 2 (в, г); 3 (а, в); 4 (а, б); 9 (а, в); 11 (а, б); 12 (в, г); 14 (а, б); 15 (а, г); 16 (б, в); 17 (а, б); 18 (в).

V. Задание на дом

§ 33 № 1 (в, г); 2 (а, б); 3 (б, г); 4 (в, г); 9 (б, г); 11 (в, г); 12 (а, б); 14 (в, г); 15 (б, в); 16 (а, г); 17 (в, г); 18 (а).

VI. Подведение итогов уроков