
Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год
Функции, их свойства и графики - Степени и корни. Степенные функции
Цель: рассмотреть свойства и графики функций ![]()
Ход уроков
I. Сообщение темы и цели уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Определение корня n-й степени из неотрицательного числа.
2. Решите уравнение (неравенство):
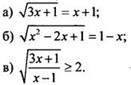
Вариант 2
1. Определение корня нечетной степени из отрицательного числа.
2. Решите уравнение (неравенство):
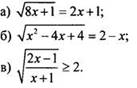
III. Изучение нового материала
Сначала
обсудим свойства функции ![]() для
неотрицательных значений аргумента. Степенная функция у = хn при
х ∈ [0; +∞) монотонна. Поэтому такая функция обратима. Найдем
обратную функцию. Из равенства у = хn выразим переменную х и
получим
для
неотрицательных значений аргумента. Степенная функция у = хn при
х ∈ [0; +∞) монотонна. Поэтому такая функция обратима. Найдем
обратную функцию. Из равенства у = хn выразим переменную х и
получим ![]() Поменяем
переменные х и у местами и получим функцию
Поменяем
переменные х и у местами и получим функцию ![]() ,
обратную для функции у = хn. Поэтому график функции
,
обратную для функции у = хn. Поэтому график функции ![]() симметричен
графику функции у = хn относительно прямой у = х для х ≥
0.
симметричен
графику функции у = хn относительно прямой у = х для х ≥
0.
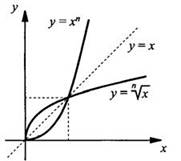
Перечислим
основные свойства функции ![]() (х
≥ 0):
(х
≥ 0):
1) область определения D(f) = [0; +∞).
2) функция не является ни четной, ни нечетной;
3) функция возрастает на [0; +∞);
4) функция ограничена снизу и не ограничена сверху;
5) наименьшее значение функции унаим = 0 при х = 0, наибольшего значения функция не имеет;
6) функция непрерывна;
7) область значений E(f) = [0; +∞);
8) функция выпукла вверх;
9) функция дифференцируема (имеет производную) в любой точке х > 0 и не имеет производной в точке х = 0.
Пример 1
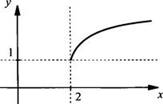
Построим
график функции ![]()
Построим
вспомогательную систему координат с началом в точке (2; 1) и осями – прямыми y
= 1 и х = 2. В этой новой системе координат построим график функции ![]()
Можно
было также сместить график функции ![]() на
две единицы вправо и на одну единицу вверх.
на
две единицы вправо и на одну единицу вверх.
Пример 2
Решим
уравнение ![]()
В
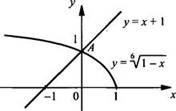
одной системе координат построим графики функций ![]() и
у = х + 1. Видно, что графики функций пересекаются в единственной точке А(0;
1). Проверка показывает, что эта точка принадлежит и графику функции
и
у = х + 1. Видно, что графики функций пересекаются в единственной точке А(0;
1). Проверка показывает, что эта точка принадлежит и графику функции ![]() , и
графику функции у = х + 1. Тогда данное уравнение имеет единственный корень: х
= 0 - абсцисса точки А.
, и
графику функции у = х + 1. Тогда данное уравнение имеет единственный корень: х
= 0 - абсцисса точки А.
Графический
способ решения подсказывает и аналитическое решение. Легко проверить, что x = 0
— корень данного уравнения. При этом функция у = х + 1 возрастает, а
функция ![]() убывает.
Тогда данное уравнение имеет только один корень.
убывает.
Тогда данное уравнение имеет только один корень.
Пример 3
Решим
неравенство ![]()
Сначала
построим график функции ![]() .
Очевидно, что у ≥ 0. Возведем обе части равенства в квадрат: у2 =
4х - х2 - и приведем его к виду (х2 - 4х + 4) +
у2 = 4 или (x - 2)2+ у2 = 22.
Видно, что графиком функции
.
Очевидно, что у ≥ 0. Возведем обе части равенства в квадрат: у2 =
4х - х2 - и приведем его к виду (х2 - 4х + 4) +
у2 = 4 или (x - 2)2+ у2 = 22.
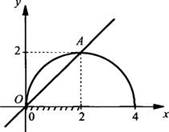
Видно, что графиком функции ![]() является
верхняя полуокружность радиуса 2 с центром в точке (2; 0). Графиком функции у =
х является биссектриса I и III координатных углов. Видно, что графики функций
пересекаются в точках O(0; 0) и А(2; 2) и данное неравенство выполняется на
промежутке х ∈ [0; 2].
является
верхняя полуокружность радиуса 2 с центром в точке (2; 0). Графиком функции у =
х является биссектриса I и III координатных углов. Видно, что графики функций
пересекаются в точках O(0; 0) и А(2; 2) и данное неравенство выполняется на
промежутке х ∈ [0; 2].
Остановимся
теперь на свойствах функции ![]() в
случае нечетного значения n и любых значений аргумента x. Очевидно,
что такая функция является нечетной. Действительно, получаем:
в
случае нечетного значения n и любых значений аргумента x. Очевидно,
что такая функция является нечетной. Действительно, получаем: ![]() Так
как выполнено равенство у(-х) = -у(х), то функция
Так
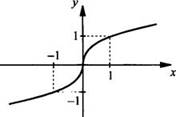
как выполнено равенство у(-х) = -у(х), то функция ![]() нечетная
и ее график симметричен относительно начала координат. На рисунке приведен
график этой функции.
нечетная
и ее график симметричен относительно начала координат. На рисунке приведен
график этой функции.
Перечислим
основные свойства функции ![]() для
нечетного значения n:
для
нечетного значения n:
1) область определения D(f) = (-∞; +∞);
2) функция нечетная и ее график симметричен относительно начала координат;
3) функция возрастает на (-∞; +∞);
4) функция не ограничена;
5) функция наименьшего и наибольшего значения не имеет;
6) функция непрерывна;
7) область значений E(f) = (-∞; +∞);
8) функция выпукла вниз на промежутке (-со; 0] и выпукла вверх на промежутке [0; +∞);
9) функция дифференцируема (имеет производную) в любой точке х ≠ 0 и не имеет производной в точке х = 0.
Пример 4
Решим
неравенство ![]()
В
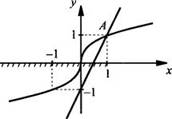
одной системе координат построим графики функций ![]() и
у = 2х - 1. Графики функций пересекаются в единственной точке А(1; 1), и данное
неравенство выполняется на промежутке х ∈(-∞;
1].
и
у = 2х - 1. Графики функций пересекаются в единственной точке А(1; 1), и данное
неравенство выполняется на промежутке х ∈(-∞;
1].
Пример 5
Построим
и прочитаем график функции у = f(х), где ![]()
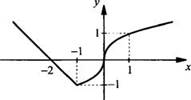
Сначала
построим график функции у = -х - 2 на промежутке (-∞; -1). Затем строим
график функции ![]() на
промежутке [-1; +∞). С учетом построенного графика перечислим основные
свойства функций:
на
промежутке [-1; +∞). С учетом построенного графика перечислим основные
свойства функций:
1) область определения D(f) = (-∞; +∞);
2) функция не является ни четной, ни нечетной;
3) функция убывает на (-∞; 1] и возрастает на [-1; +∞);
4) функция ограничена снизу и не ограничена сверху;
5) наименьшее значение функции унаим = -1 при х = -1, наибольшего значения функция не имеет;
6) функция непрерывна;
7) область значений E(f) = [-1; +∞);
8) функция выпукла вниз на промежутке [-1; 0] и выпукла вверх на промежутке [0; +∞);
9) функция дифференцируема (имеет производную) в любой точке х, кроме х = -1 и х = 0. Не имеет производной в точках х = -1 и х = 0.
Пример 6
Найдем
область определения и область значений функции: ![]()
а) Область определения функции задается условием 4х2 - 9 ≥ 0. Решение этого неравенства D(f) = (-∞; -1,5] U [1,5; +∞). В этих промежутках функция принимает значения E(f) = [0; +∞).
б) Функция определена при всех значениях х, т. е. D(f) = (-∞; +∞). При этом сама функция также принимает все значения, т. е. E(f) = (-∞; +∞).
в)
Область определения функции задается условиями х - 2 ≥ 0 и х2 +
5 ≥ 0. Решение этой системы неравенств D(f) = [2; +∞). В этом
промежутке функции х – 2 ≥ 0 и х2 + 5 возрастающие. При
этом х - 2 ≥ 0 и х2 + 5 ≥ 9, тогда ![]() и
и ![]()
![]() Поэтому
область значений данной функции E(f) = [12; +∞).
Поэтому
область значений данной функции E(f) = [12; +∞).
IV. Контрольные вопросы
1.
Приведите свойства и график функции ![]()
2.
Перечислите свойства и приведите график функции ![]() для
нечетных n.
для
нечетных n.
V. Задание на уроках
§ 34, № 1 (а, б); 3 (а); 4 (а, б); 5 (в, г); 6; 8 (а, б); 10 (в, г); 12; 14 (а, б); 15 (а); 16 (в); 17 (а, б); 18 (в); 19 (а, б); 21 (а); 22 (б).
VI. Задание на дом
§ 34, № 1 (в, г); 3 (в); 4 (в, г); 5 (а, б); 7; 8 (в, г); 10 (а, б); 13; 14 (в, г); 15 (б); 16 (г); 17 (в, г); 18 (а); 19 (в, г); 21 (б); 22 (а).
VII. Подведение итогов уроков
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.