алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Свойства корня n-й степени - Степени и корни. Степенные функции

Цель: обсудить основные свойства корней и их применение к решению задач.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Найдите область определения функции:

2. Постройте график функции:

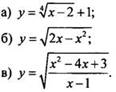
Вариант 2

1. Найдите область определения функции:

2. Постройте график функции:

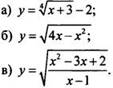
III. Изучение нового материала

Для вычисления иррациональных выражений необходимо знать свойства корней n-й степени и уметь ими пользоваться.

Теорема 1. Корень n-й степени (n = 2, 3, 4, ...) из произведения двух неотрицательных чисел равен произведению корней n-й степени из этих чисел, т. е. 

Докажем это утверждение. Для удобства введем обозначения:  Надо доказать, что для неотрицательных чисел х, у, z выполнено равенство х = y ∙ z. При введенных обозначениях имеем:  тогда  или  откуда х = y ∙ z. Это и требовалось доказать.

Пример 1

Вычислим: 

Разумеется, приведенную формулу можно применять слева направо и справа налево.

Пример 2

Вычислим:  

Теорема 2. Корень n-й степени из отношения неотрицательного числа а и положительного числа b равен отношению корней n-й степени из этих чисел, т. е. 

Докажем такое утверждение. Пусть 

Надо доказать, что для неотрицательных чисел х и у и положительного числа z выполнено равенство . При введенных обозначениях получаем:  тогда  или  откуда . Таким образом, утверждение доказано.

Пример 3

Вычислим: 

Пример 4

Найдем: 

Пример 5

Вычислим 

Прежде всего обратим смешанное число  в неправильную дробь:  Теперь, используя теорему 2, найдем: 

Разумеется, теоремы 1 и 2 являются обобщениями аналогичных свойств квадратных корней (8 класс). Рассмотрим теперь другие свойства радикалов.

Теорема 3. Чтобы возвести корень n-й степени из неотрицательного числа а в натуральную степень k, надо в эту степень возвести подкоренное выражение, т. е.  Очевидно, что такое утверждение является следствием теоремы 1. Действительно, получаем: 

Пример 6

Вычислим: 

Теорема 4. Чтобы извлечь корень n-й степени из корня k- й степени из неотрицательного числа а, надо извлечь корень степени nk из этого числа, т. е. 

Докажем это утверждение. Обозначим  Надо доказать, что для неотрицательных чисел х и у выполнено равенство х = у. Возведем в n-ю степень х и получим:  Теперь такое равенство возведем в степень k. Имеем: (хⁿ)^k = а или х^nk = а. Также возведем в степень nk величину у и получим: у^nk = а. Очевидно, что x^nk = у^nk, и тогда х = у.

Утверждение доказано.

Пример 7

Упростим выражение:

Теорема 5. Если показатели корня и подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится, т. е. 

Обозначим  (тогда по определению корня выполнено равенство x^np = a^kp) и  (тогда имеем уⁿ = а^k). Возведем в степень р обе части последнего равенства: у^nр =а^kp. Сравнивая равенства х^nр = а^kр и у^nр = а^kp, получаем х^nр = у^nр, откуда х = у (что и требовалось доказать).

Пример 8

а)  (показатели корня и подкоренного выражения разделили на 4);

б)  (показатели корня и подкоренного выражения умножили на 2).

Пример 9

Упростим выражение 

Каждый корень, входящий в выражение, представим в виде корня степени 12 (теорема 5) и учтем теорему 1. Получаем:  

IV. Контрольные вопросы (фронтальный опрос)

1. Сформулируйте (и докажите) теорему о корне из произведения чисел.

2. Сформулируйте (и докажите) теорему о корне из частного двух чисел.

3. Возведение корня из числа в натуральную степень.

4. Извлечение корня из корня числа.

V. Задание на уроках

§ 35, № 1 (а, г); 4 (а, б); 9 (а, г); 10 (б); 12 (а, б); 13 (б); 14 (а, в); 15 (б); 16 (а); 19 (б, в); 20 (а, б); 22 (в, г); 24 (а, г); 26 (б); 28; 30 (а, в).

VI. Задание на дом

§ 35, № 1 (б, в); 4 (в, г); 9 (б, в); 10 (г); 12 (б, г); 13 (а); 14 (б, г); 15 (а); 16 (б); 19 (а, г); 20 (в, г); 22 (а, б); 24 (б, в); 26 (а); 29; 30 (б, г).

VII. Подведение итогов уроков