алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Преобразование выражений, содержащих радикалы - Степени и корни. Степенные функции

Цель: рассмотреть свойства корней и их использование для преобразования выражений.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Корень из произведения двух чисел (с доказательством).

2. Вычислите: 

3. Упростите выражение 

Вариант 2

1. Корень из частного двух чисел (с доказательством).

2. Вычислите: 

3. Упростите выражение 

III. Изучение нового материала

Приведем полученные на прошлом уроке основные свойства корня n-й степени:

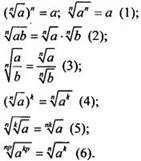
Приведенные формулы используют для преобразования выражений, содержащих корни (радикалы). Такие выражения называют иррациональными. Рассмотрим наиболее типичные примеры.

Пример 1

Сравним числа:

а)  Представим данные корни в виде корней одной и той же степени, используя свойство 5. Получаем:  и  Так как 9 > 8 > 0, то имеем  или 

б)  (при a > 1, n ∈ N и n ≥ 2). Используя свойство 5, представим данные корни в виде корней одинаковой степени. Получаем:  Так как  то имеем  или 

Во многих случаях требуется выполнять операции вынесения из-под корня и внесения под корень некоторых выражений. В случае корней четной степени учащиеся, как правило, допускают ошибки.

Еще раз напомним, что  если n - четное натуральное число.

Пример 2

а) Вынесем множитель за знак корня 

Учтем ОДЗ данного выражения: a - любое действительное число, b ≥ 0. Используя свойства корней, получаем:   (учтем, что 

б) Внесем множитель под знак корня 

ОДЗ данного выражения: b ≥ 0 и a - любое действительное число. Поэтому необходимо рассмотреть два случая:

если a ≥ 0, то 

если а < 0, то -а = |а| и  

Итак, данное выражение 

Понятие корня n-й степени необходимо и в преобразованиях выражений.

Пример 3

Упростим числовое выражение:

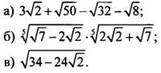
а) Вынесем множители за знаки корней. Получаем: 

б) Используем свойство произведения корней и формул разности квадратов. Имеем: 

в) Предположим, что подкоренное выражение  является квадратом разности, т. е.  где а и b - некоторые положительные числа. Возведем в квадрат правую часть равенства:  Приравняем целую и иррациональную части. Получаем систему уравнений  Решением этой системы являются числа а = 4 и b = 3. Таким образом, 

 Было учтено, что √2 ≈ 1,4 и 

В ряде случаев полезно избавляться от корней (иррациональности) в знаменателях дробей. Для этого используют формулы сокращенного умножения.

Пример 4

Избавимся от иррациональности в знаменателе дроби 

Запишем знаменатель дроби в виде  Очевидно, что такое выражение является неполным квадратом разности чисел  Поэтому умножим числитель и знаменатель данной дроби на сумму  (сопряженную величину) и учтем формулу суммы кубов. Получаем: 

Этот же прием можно использовать и для решения более сложных задач.

Пример 5

Найдем сумму дробей 

Избавимся в сумме А от иррациональности в знаменателях дробей:

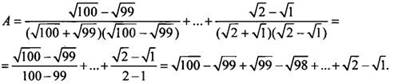
Так как в рассматриваемой сумме сокращаются все слагаемые, кроме первого и последнего, то она равна 

Пример 6

У простим выражение 

Для того чтобы A было определено, необходимо выполнить условия: 1 - х ≥ 0, 4х² - 12х + 9 ≥ 0. Первое из них выполнено для х ≤ 1, второе - для всех х, так как 4х² – 12x + 9 = (2х - 3)² ≥ 0. Тогда выражение А имеет вид:  Раскрывая знак абсолютной величины для х ≤ 1 (а при таких х выражение 2х - 3 < 0), имеем: 

Из приведенного примера видно, что в рассматриваемых выражениях успешно используются формулы сокращенного умножения. Рассмотрим еще один пример.

Пример 7

Упростим выражение  Под каждым из радикалов, входящих в А, находится полный квадрат суммы чисел, что, однако, является неочевидным. Чтобы убедиться в этом, введем новую переменную   Подставив это выражение в А, получим: 

 Так как арифметический корень у ≥ 0, то выражения у + 1 и 2у + 1 положительны. Поэтому  Это выражение определено при х ≥ 5/3.

Заметим, что во многих случаях выражения, содержащие радикалы, с помощью простейших замен сводятся к алгебраическим рациональным выражениям.

Пример 8

Упростим выражение 

Введем очевидные замены  тогда х = у² и а = z². Подставив х и а в выражение А, получим: 

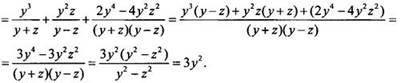
Возвращаясь к исходным переменным х и а, найдем А = 3x. Это выражение А определено при х ≥ 0, а ≥ 0, х ≠ а.

IV. Задание на уроках

§ 36, № 1; 6 (а, б); 8 (в, г); 9 (а, г); 11 (а, б); 12 (г); 13 (б); 14 (в); 16 (г); 17 (а); 19 (б); 23 (г); 24 (а, б); 27 (в, г); 29 (а); 30 (б).

V. Задание на дом

§ 36, № 2; 6 (в, г); 8 (а, б); 9 (б, в); 11 (в, г); 12 (б); 13 (г); 14 (а); 16 (б); 17 (в); 19 (г); 23 (б); 24 (в, г); 27 (а, б); 29 (б); 30 (а).

VI. Подведение итогов уроков