алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Иррациональные уравнения и неравенства (факультативное занятие) - Степени и корни. Степенные функции

Цель: рассмотреть основные типы иррациональных уравнений и неравенств и способы их решения.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Сравните числа: 

2. Упростите выражение  (при а ≤ 0).

3. Решите неравенство (х⁴ - 2)(х³ + 1) ≤ 0.

Вариант 2

1. Сравните числа: 

2. Упростите выражение  (при а ≤ 0).

3. Решите неравенство (х⁶ - 3)(х³ + 8) ≤ 0.

III. Изучение нового материала

Уравнение (неравенство), в котором под знаком корня содержится переменная, называют иррациональным.

Пример 1

а) Уравнения и неравенства   являются иррациональными, т. к. под знаком радикала находится переменная.

б) Уравнения и неравенства:  не являются иррациональными, т. к. переменная не находится под знаком корня. Отметим, что под знаками корня содержатся какие-то числа. При этом первое уравнение и второе неравенство являются квадратными. Третье уравнение и четвертое неравенство являются линейными.

Введем два важнейших понятия, полезных при решении иррациональных уравнений и неравенств. Первое из них - область допустимых значений (ОДЗ) - вам уже знакомо. ОДЗ называется множество значений переменной, при которых уравнение или неравенство имеет смысл. В рассматриваемой теме ОДЗ, как правило, определяется возможностью извлечения корня четной степени из выражений.

Пример 2

ОДЗ уравнения  задается неравенствами  решение которых 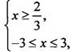 откуда  Этот промежуток является ОДЗ данного уравнения.

В ряде случаев нахождения ОДЗ позволяет решить уравнение или неравенство.

Пример 3

Решим неравенство 

ОДЗ данного неравенства задается условиями  Решение этих неравенств  откуда х = 4. Видно, что ОДЗ неравенства состоит из одной точки х = 4. Проверим, является ли это число решением данного неравенства. Подставим его в неравенство и получим:  или 0 ≥ -1. Получили верное неравенство. Поэтому решение данного неравенства - число х = 4.

Другим важным понятием при решении является область существования решений (ОСР), т. е. множество значений переменной, при которых решение уравнения или неравенства возможно.

Пример 4

Рассмотрим уравнение 

В левой части уравнения находится арифметический корень четной степени. По определению эта величина неотрицательная. Поэтому в правой части уравнения может стоять только неотрицательное выражение. Получаем условие х - 2 ≥ 0, которое определяет ОСР. Следовательно, ОСР данного уравнения - все значения х из промежутка [2; ∞).

Очевидно, что решение иррационального уравнения или неравенства может находиться только в множестве значений переменной, которое является пересечением ОДЗ и ОСР.

Пример 5

Решим неравенство 

ОДЗ неравенства задается условием -х² + 6х – 8 ≥ 0, решение которого х ∈ [2; 4]. Так как в левой части данного неравенства находится неотрицательная величина (арифметический корень четной степени), то и правая часть должна быть неотрицательной: х - 5 ≥ 0, откуда х ∈ [5; ∞) - ОСР. Видно, что пересечение ОДЗ и ОСР неравенства является пустым множеством. Поэтому данное неравенство решений не имеет.

Заметим, что одним из приемов решения иррациональных уравнений и неравенств является возведение в степень обеих частей. В случае уравнений такая операция может привести к появлению посторонних корней, которые легко удаляются при проверке. При решении неравенств необходимо внимательно контролировать ОДЗ и ОСР. Полезно сочетать аналитическое решение с графическим как в случае уравнений, так и в случае неравенств.

Остановимся сначала на основных типах иррациональных уравнений и способах их решения. Систематизация этих типов весьма условна.

1. Уравнения с одним знаком радикала

Пример 6

Решим уравнение 

Запишем уравнение в виде  и решим его двумя способами. Учтем, что для уравнения ОДЗ х ∈ [7/2; ∞) и ОСР х ∈ [21; ∞). Поэтому корни уравнения могут находиться только в промежутке х ∈ [21; ∞).

1-й способ. Возведем обе части уравнения в квадрат: 2x - 7 = x² - 42х + 441 или 0 = х² - 44х + 448. Корни этого квадратного уравнения x₁ = 28 и x₂ = 16. Для данного иррационального уравнения корень х = 16 является посторонним, т. к. не входит в ОСР.

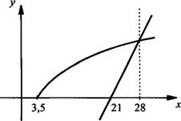
Для иллюстрации построим графики функций  и у₂ = х - 21. Видно, что эти графики пересекаются в единственной точке, абсцисса которой x = 28 и является корнем данного уравнения.

Недостаток этого способа решения - достаточно громоздкие коэффициенты полученного квадратного уравнения 0 = х² - 44х + 448.

2-й способ. Введем новую переменную  (где t ≥ 0) и выразим х:  Тогда данное уравнение имеет вид:  или 0 = t² – 2t - 35 (заметим, что коэффициенты этого квадратного уравнения небольшие), корни которого t₁ = 7 и t₂ = -5 (не подходит, т. к. t ≥ 0). Вернемся к старой переменной и найдем корень данного уравнения: 

Из приведенного примера видно, что эффективным приемом является использование новой переменной (замена переменной).

Пример 7

Решим уравнение 

Введем новую переменную  (где t ≥ 0) и выразим соотношение х² - 4х. Имеем: t² = х² - 4х + 20, откуда х² - 4х = t² - 20. Тогда данное уравнение имеет вид: t² – 20 – 3t + 10 = 0 или t² – 3t - 10 = 0. Корни этого уравнения t₁ = 5 и t₂ = -2 (не подходит, т. к. t ≥ 0). Вернемся к старой переменной и получим квадратное уравнение 5² = х² - 4х + 20 или 0 = х² - 4х - 5, корни которого x₁ = 5 и х₂ = -1. Оба этих корня являются также корнями исходного уравнения.

2. Уравнения с двумя знаками радикала

Пример 8

Решим уравнение 

Обсудим способы решения подобных уравнений.

1-й способ. Такой способ является традиционным и состоит в уединении радикала и возведении обеих частей уравнения в степень. Отметим, что ОДЗ уравнения х ∈ [-1; ∞). Запишем уравнение в виде  и возведем обе части уравнения в квадрат:  Тогда  Вновь возведем обе части уравнения в квадрат: (х + 1)² = 4(х + 1) или (х + 1)(х - 3) = 0. Корни того уравнения x₁ = -1 и х₂ = 3 также являются решениями данного уравнения.

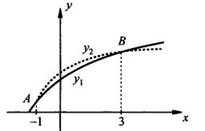
Проиллюстрируем наше решение графически. Построим графики функций  (сплошная линия) и  (штрихпунктирная линия). Видно, что графики имеют две общие точки А и В, абсциссы х₁ = -1 и х₂ = 3 которых являются корнями иррационального уравнения.

2-й способ. Введем новую переменную  (где t ≥ 0). Тогда t² = х + 1 и х = t² - 1. Данное уравнение имеет вид:  и представляет собой уравнение уже с одним радикалом. Далее его можно решить, например, традиционным способом. Запишем уравнение в виде  и возведем в квадрат обе части уравнения: 2t² + 1 = t² + 2t + 1 или t(t - 2) = 0. Корни такого уравнения t₁ = 0 и t₂ = 2 удовлетворяют условию t ≥ 0. Теперь найдем x₁ = 0 - 1 = -1 и х₂ = 2² - 1 = 3.

3-й способ. Введем две новые переменные  (где а, b ≥ 0). Тогда одно уравнение легко записать сразу: а - b = 1. Чтобы получить второе уравнение, возведем величины а и b в квадрат: а² = 2х + 3 и b² = х + 1. Для исключения переменной х умножим второе соотношение на 2 и вычтем из первого: а² - 2b² = 1. Таким образом, исходное иррациональное уравнение свелось к системе алгебраических уравнений  При этом для нахождения х достаточно найти любую из величин а или b.

Из первого уравнения выразим a = b + 1 и подставим во второе: (b + 1)² - 2b² = 1 или 0 = b(b - 2). Корни этого уравнения b₁ = 0 и b₂ = 2 удовлетворяют условию b ≥ 0 (тогда a = b + 1 тем более положительно). Находим х = b² - 1 и получаем: х₁ = -1 и х₂ = 3.

Последний способ решения полезен и в случае уравнений других типов.

3. Однородные иррациональные уравнения

Пример 9

Решим уравнение 

Так как в уравнение входят корни нечетной степени, то х может быть любым действительным числом. Введем новые переменные  Тогда уравнение имеет вид: а² – 3b² = 2abили a² - 2ab - 3b² = 0. Левая часть этого уравнения представляет собой однородный многочлен второй степени по переменным а и b. Решая полученное квадратное уравнение (считая, что a - неизвестная, b - постоянная величина), найдем a = -b и а = 3b. Вернемся к неизвестной х. Имеем два случая:

а) a = -b или  Возведем обе части уравнения в куб: х - 1 = -(х + 1) - и найдем x₁ = 0;

б) а = 3b или  Обе части уравнения возводим в куб: х - 1 = 27(х + 1) - и находим 

Итак, данное иррациональное уравнение имеет два корня: х₁ = 0 и х₂ = -14/13.

4. Уравнения с радикалами больших степеней

Пример 10

Решим уравнение 

Очевидно, что х может быть любым действительным числом. Введем новые переменные  Запишем первое уравнение a + b = 3. Чтобы получить второе уравнение, возведем в куб величины а и b и получим: а³ = 3х - 1 и b³ = 2х - 5. Для исключения переменной х умножим первое равенство на 2, второе - на 3: 2а³ = 6х - 2 и 3b³ = 6х - 15 - и вычтем эти соотношения: 2а³ – 3b³ = 13. Таким образом, исходное иррациональное уравнение свелось к системе алгебраических уравнений 

Из первого уравнения выразим b = 3 - а и подставим во второе: 2а³ - 3(3 - а)³ = 13 или 5a³ - 27а² + 81а - 94 = 0. Это кубическое уравнение имеет единственный действительный корень а = 2, Находим  Итак, данное уравнение имеет одно решение х = 3.

5. Уравнения с громоздкими радикалами

Пример 11

Решим уравнение 

Каждое подкоренное выражение является полным квадратом. Однако это далеко не очевидно. Введем две новые переменные  (где х ≥ 2). С помощью этих величин выразим переменную х: х = а² - 1 и х = b² + 2. Тогда уравнение имеет вид  или  или |а + 1| + |b - 3| = 5, или а + 1 + |b - 3| = 5 (учтено, что а ≥ 0), или а + |b- 3| = 4. В полученном равенстве раскроем знак модуля и вернемся к неизвестной х.

а) Если b - 3 < 0 (т. е. b < 3 или ), то равенство имеет вид: а - b + 3 = 4, или а = b + 1, или  Возведем в квадрат обе части этого уравнения:  или  (при этом выполнено условие ). Тогда 1 = х - 2 и х = 3 - корень исходного иррационального уравнения.

б) Если b - 3 ≥ 0 (т. е. b ≥ 3 или ), то равенство имеет вид: а + b - 3 = 4, или а + b = 7, или а = 7 - b, или  Возведем в квадрат обе части этого уравнения:  или  откуда  (при этом выполнено условие ). Возведем в квадрат обе части такого уравнения:  откуда  - также корень данного уравнения.

6. Уравнения, в которых важна группировка членов

Даже в достаточно сложных уравнениях традиционный способ решения (возведение в степень) дает хорошие результаты, если предварительно сделать группировку членов уравнения.

Пример 12

Решим уравнение 

Учтем ОДЗ: х ∈ [-1; ∞) - и запишем уравнение в виде  учитывая коэффициенты при неизвестной. Возведем в квадрат обе части:  или  Очевидно, что уравнение имеет два корня: х₁ = -4 (не входит в ОДЗ) и х₂ = -1. Итак, исходное иррациональное уравнение имеет единственный корень х = -1.

В заключение этой части занятия еще раз отметим полезность и целесообразность введения новых переменных (замен неизвестных), рассмотрев следующий пример.

Пример 13

Решим уравнение 

Понятно, что возведение в куб обеих частей уравнения ничего не дает, т. к. возникает уравнение девятой степени. Поэтому введем новую неизвестную  Сразу можно написать первое уравнение: х³ + 1 = 2t. Чтобы получить второе уравнение, возведем в куб выражение для величины t: t³ = 2х - 1 или t³ + 1 = 2х. Получим систему алгебраических уравнении 

Вычтем уравнения друг из друга: х³ - t³ = 2(t - х). Перенесем все члены уравнения в левую часть и разложим ее на множители:  или  Произведение множителей равно нулю, если один из них равен нулю. Получаем: х - t = 0 (т. е. х = t) и  (это уравнение не имеет решений, т. к. дискриминант  при всех значениях t). Подставим t = х в первое уравнение системы и получим кубическое уравнение: х³ + 1 = 2х или х³ - 2х + 1 = 0, которое имеет корни x₁ = 1 и  Эти корни являются также решениями данного иррационального уравнения.

IV. Контрольные вопросы

1. Какие уравнения (неравенства) называются иррациональными? Приведите примеры.

2. Дайте определение области допустимых значений (ОДЗ) уравнения или неравенства.

3. Что называется областью существования решений (ОСР) уравнения или неравенства?

V. Творческие задания (на уроках и дома)

Решите уравнения:

VI. Подведение итогов уроков