алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Системы иррациональных уравнений. Иррациональные неравенства (факультативное занятие) - Степени и корни. Степенные функции

Цели: рассмотреть наиболее типичные системы иррациональных уравнений; обсудить решение иррациональных неравенств.

Ход уроков

I. Сообщение темы и целей уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Дайте определение области допустимых значений (ОДЗ) уравнения или неравенства. Приведите примеры.

2. Решите уравнения:

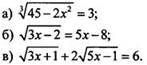
Вариант 2

1. Дайте определение области существования решений (ОСР) уравнения или неравенства. Приведите примеры.

2. Решите уравнения:

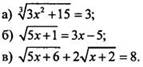
III. Изучение нового материала

Прежде всего остановимся на системах иррациональных уравнений. Как правило, такие системы решатся с помощью замены переменных (или переменной).

Пример 1

Решим систему уравнении 

Введем две новые переменные  Тогда получим систему алгебраических уравнений  Левую часть второго уравнения разложим на множители  и подставим первое уравнение во второе. Приходим к симметричной системе уравнений  Из первого уравнения выразим b = 3 - а и подставим во второе. Получаем: а² - а(3 - а) + (3 - а)² = 3 или а² - 3а + 2 = 0. Корни этого уравнения а₁ = 1 и а₂ = 2. Соответствующие значения b₁ = 2 и b₂ = 1. Вернемся к старым переменным и получим две простейшие системы уравнении:  (решение х = 1, у = 8) и  (решение х = 8, у = 1). Таким образом, данная система уравнений имеет два решения: (1; 8) и (8; 1).

Пример 2

Решим систему уравнений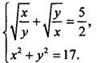 

Сначала рассмотрим первое уравнение. Введем для него новую неизвестную  Тогда уравнение имеет вид:  или 2t² - 5t + 2 = 0. Корни этого уравнения t₁ = 2 (тогда  и x = 4y) и t₂ = 1/2 (откуда  и y = 4x).

Вернемся к старым переменным и получим системы алгебраических уравнений:  (решения х = 4, у = 1 и х = -4,у = -1) и  (решения х = 1, у = 4 и х = -1, у = -4). Таким образом, исходная система имеет четыре решения: (4; 1), (-4; -1), (1; 4), (-1; -4).

Достаточно часто при решении систем иррациональных уравнений их необходимо преобразовать и найти более простую связь между неизвестными.

Пример 3

Решим систему уравнений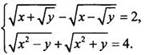 

Возведем первое уравнение в квадрат и получим:  или  Учтем, что х - 2 ≥ 0 (т. е. х ≥ 2 - ОСР), и вновь возведем обе части уравнения в квадрат: х² - 4х + 4 = х²- у, откуда у = 4х - 4. Таким образом, нашли линейную связь между неизвестными х и у.

Подставим соотношение у = 4x - 4 во второе уравнение системы:  или  или  (учтено, что х ≥ 2 и |х - 2| = х - 2), откуда  (заметим, что х ≤ 6 - ОСР). Возведем в квадрат, обе части уравнения:  - и найдем  которое удовлетворяет условиям 2 ≤ х ≤ 6. Теперь определим  Итак, данная система имеет единственное решение (5/2; 6).

Обратимся теперь к иррациональным неравенствам. Если в случае уравнений и систем уравнений, как правило, было конечное число решений (и их можно было легко проверить подстановкой), то в случае неравенств решением являются числовые промежутки, которые подстановкой проверить невозможно. Поэтому в иррациональных неравенствах необходимо четко контролировать ОДЗ и ОСР.

Пример 4

Решим неравенство 

ОДЗ неравенства задается условием  Так как левая часть неравенства по определению арифметического корня неотрицательна, а правая часть является отрицательным числом, то ОСР - любое действительное число х. Поэтому данное неравенство выполняется при всех значениях х, которые входят в ОДЗ. Другими словами, данное неравенство равносильно неравенству  или  или  и х ≠ 3. Решая такое неравенство методом интервалов, получим: 

Запомните железное правило: обе части неравенства можно возводить в четную степень, если эти части неотрицательны.

Пример 5

Решим неравенство 

ОДЗ неравенства задается условием 6х + 4 ≥ 0, откуда х ∈ [-2/3; ∞). Так как левая часть неотрицательна, то правая часть неравенства тем более должна быть неотрицательной.

Поэтому ОСР определяется условием 3х - 2 ≥ 0, откуда х ∈ [2/3; ∞). Так как обе части неравенства неотрицательны, то возведем их в квадрат. При этом знак неравенства сохраняется. Получаем: 6х + 4 ≤ 9х² - 12х + 4 или 0 ≤ х(х - 2). Решение этого квадратного неравенства х ∈ (-∞; 0] U [2; ∞). С учетом ОДЗ и ОСР получаем решение данного иррационального неравенства х ∈ [2; ∞).

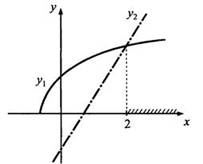
Дадим графическую иллюстрацию решения. На рисунке приведены эскизы графиков  (сплошная линия) и у₂ = 3х - 2 (штрихпунктирная линия). Видно, что неравенство у₁ ≤ у₂ (график у₁ располагается не выше графика у₂) при х ∈ [2; ∞).

Пример 6

Решим неравенство 

ОДЗ неравенства х ∈ [-7; ∞), ОСР - любое действительное число х. При этом правая часть неравенства может быть как отрицательной, так и неотрицательной. В связи с этим естественным образом возникают два случая.

а) Если х + 3 < 0, то неравенство, очевидно, выполняется при всех х, входящих в ОДЗ. Имеем систему линейных неравенств  решение которых  откуда х ∈ [-7; -3).

б) Если х + 3 ≥ 0, то имеем право возвести в квадрат обе части данного иррационального неравенства. Получаем систему неравенств:  При этом в силу второго неравенства величина 2х + 14 больше квадрата некоторого выражения и будет положительной. Поэтому решения второго неравенства (и всей системы этого случая) автоматически входят в ОДЗ. Никаких дополнительных условий записывать не надо.

Решая систему случая б, получаем:  или  Решение этих неравенств  откуда х ∈ [-3; 1).

Объединяя ответы случаев а и б, получаем окончательное решение данного иррационального неравенства х ∈ [-7; 1).

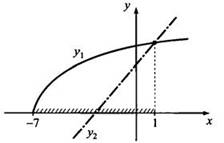
Приведем графическую интерпретацию решения неравенства. Построим эскизы графиков функций  (сплошная линия) и у₂ = х + 3 (штрихпунктирная линия). Неравенство у₁ > у₂ (т. е. график у₁ лежит выше графика y₂) выполняется при х в [-7; 1).

Разумеется, при решении иррациональных неравенств используются те же приемы, что и в случае уравнений и систем уравнений, в частности замена переменной.

Пример 7

Решим неравенство 

ОДЗ данного неравенства задается условием 5 - х > 0, откуда х < 5. Введем новую переменную  (где t > 0). Получаем неравенство  Так как величина t > 0, то умножим обе части неравенства на t. При этом знак неравенства сохраняется. Получаем квадратное неравенство: 3 - t² < 2t или 0 < t² + 2t - 3. Его решения t < -3 и t > 1. Так как t > 0, то неравенство t < -3 не выполняется. Рассмотрим неравенство t > 1 (при этом условие t > 0 выполнено) или  Возведем в квадрат обе неотрицательные части этого неравенства. Получаем: 5 - х > 1, откуда х < 4. Итак, решение данного неравенства х ∈ (-∞; 4).

Как и при решении неравенств других типов, наиболее эффективным и мощным методом решения иррациональных неравенств является метод интервалов. Однако использовать его можно только в области непрерывности рассматриваемой функции.

Пример 8

Решим неравенство 

ОДЗ неравенства задается условиями 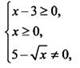 откуда х ∈ [3; 25) U (25; ∞). В этой области левая часть неравенства является непрерывной функцией. Найдем точки, в которых числитель и знаменатель дроби равны нулю. Для этого решаем уравнения  (корень х = 4) и  (решение х = 25). Отметим эти точки на числовой оси.

Определим знак величины  например, при х = 9 и получим:  Построим диаграмму знаков левой части неравенства. Теперь легко записать ответ: х ∈ [3; 4] U (25; ∞).

Метод интервалов удобно использовать, если кроме иррациональных функций в неравенство входят и функции других видов.

Пример 9

Решим неравенство 

ОДЗ неравенства задается условиями 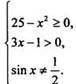 Решение первых двух неравенств дает промежуток (1/3; 5]. В этом интервале найдем точки, в которых числитель и знаменатель дроби обращаются в нуль. Получаем уравнения:  (корень х = 4) и  (решения ). Отметим эти точки на числовой прямой.

Определим знак левой части неравенства, например, в точке х = 3 и получим:  Построим диаграмму знаков дроби. На основании диаграммы выпишем ответ: 

IV. Творческие задания (на уроках и дома)

1) Решите системы иррациональных уравнений:

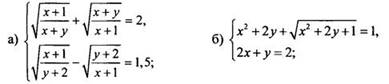
2) Решите неравенство:

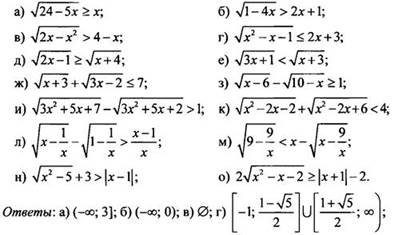
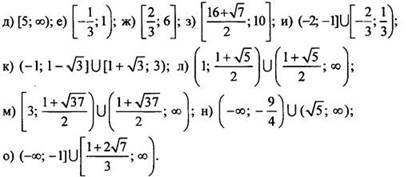
V. Подведение итогов уроков