алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Обобщение понятия о показателе степени - Степени и корни. Степенные функции

Цели: обобщить понятие степени числа; рассмотреть свойства степеней.

Ход урока

I. Сообщение темы и целей урока

II. Изучение нового материала

В более ранних классах было определено понятие степени числа с целым показателем. Выражение аⁿ имеет смысл при всех целых n и любых значениях а, кроме а = 0 и n ≤ 0.

Пример 1

а) Выражения  и т. д. определены.

б) Выражения 0^-3, 0^-7, 0⁰ не имеют смысла.

Напомним свойства таких степеней. Для любых чисел а, b и любых целых чисел m и n выполнены равенства:

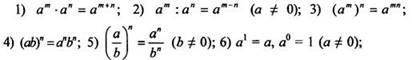
7) если m > n, то а^m > аⁿ при а > 1 и а^m <аⁿ при 0 < а < 1.

Теперь необходимо понять смысл выражений  и т. д. Для этого надо таким образом обобщить понятие степени, так чтобы выполнялись все или часть перечисленных свойств степеней. Рассмотрим равенство  Тогда по определению корня q-й степени разумно считать, что  будет корнем q-и степени из числа а^p.

Итак, степенью числа а > 0 с рациональным показателем  (где р - целое число, q - натуральное (q > 1)) называется число  т. е.  При этом степень числа 0 определена только для положительных показателей, т. е. 0^r = 0 для любого r > 0.

Пример 2

По определению степени с рациональным показателем и свойствам корней получаем: 

Сделаем ряд замечаний, связанных с понятием степени с рациональным показателем.

1) Для любого а > 0 и любого рационального числа r число а^r > 0.

2) По основному свойству дробей рациональное число можно записать в виде  для любого натурального числа k. Тогда значение степени не зависит от формы записи рационального числа, т. к. 

3) При а < 0 рациональная степень числа а не определена. Поясним это примером. Рассмотрим  С другой стороны,  и тогда  Получаем противоречие.

Для приведенного определения степени с рациональным показателем выполняются все приведенные ранее основные свойства степеней, но только для положительных оснований.

Итак, для любых рациональных чисел s и t и любых положительных чисел а и b справедливы равенства:

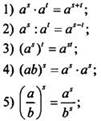
6) если 0 < a < b, to a^s <b^sпри s > 0 и a^s > b^sпри s < 0;

7) если s > t, to a^s > b^tпри a > a^tи a^s < a^tпри 0 < a < 1.

Перечисленные свойства доказываются исходя из определения степени с рациональным показателем, свойств корней и свойств степени с целым показателем.

Пример 3

Докажем свойство 1.

Пусть  где n и l - натуральные числа, m и k - целые. Тогда получаем: 

Аналогично доказывают свойства 2-5.

Пример 4

Докажем свойство 6.

Запишем число S > 0 в виде  где m и n - натуральные числа. Из неравенства 0 < a < b и свойств степени с целым показателем следует, что а^m < b^m. По свойству корней из такого неравенства получаем:  или  или а^s< b^s.

Случай S < 0 рассматривается аналогично.

Обсудим применение приведенных свойств.

Пример 5

Вычислим выражение 

Используя свойства степени с рациональным показателем, запишем выражение в виде 

Пример 6

Упростим выражение 

Перейдем к рациональным показателям степени и получим: 

Пример 7

Вычислим выражение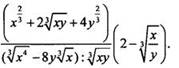 

Используем определение рационального показателя степени и свойства степеней. Имеем: 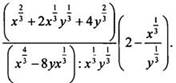 Для удобства введем новые переменные  и получим:

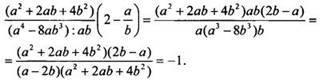
В этом примере оказалось целесообразным использование новых переменных, т. к. это сразу позволило перейти к выражению с натуральными показателями степени, с которым удобнее проводить преобразования.

Пример 8

Сравним числа 

Число  запишем в виде степени с рациональным показателем  Так как  то по последнему свойству степеней  или 

III. Контрольные вопросы

1. Дайте определение степени числа с рациональным показателем.

2. В каком случае определена степень числа О?

3. Перечислите основные свойства степеней числа (фронтальный опрос).

IV. Задание на уроке

§ 37, No 1 (а, б); 2 (г); 5 (в, г); 7 (а, б); 9; 14 (а, в); 19 (в, г); 24 (а, г); 26 (б); 27 (а, б); 28 (в, г); 30 (а, б); 32 (а); 33 (б).

V. Задание на дом

§ 37, № 1 (в, г); 2 (а); 6 (б, в); 7 (в, г); 10; 14 (б, г); 19 (а, б); 24 (б, в); 26 (г); 27 (в, г); 29 (б); 30 (в, г); 32 (б); 33 (а).

VI. Подведение итогов урока