алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Степенные функции, их свойства и графики - Степени и корни. Степенные функции

Цели: обобщить понятие степенной функции; рассмотреть свойства и графики таких функций.

Ход урока

I. Сообщение темы и целей урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (тест).

Вариант 1

1. Найдите значение выражения: 

Ответы: 

2. Упростите выражение: 

Ответы: 

3. Сократите дробь: 

Ответы: 

Вариант 2

1. Найдите значение выражения: 

Ответы: 

2. Упростите выражение: 

Ответы: 

3. Сократите дробь: 

Ответы: 

III. Изучение нового материала

Функции вида у = x^r (где r - любое действительное число (в том числе и иррациональное)) называют степенными функциями. Пока будем рассматривать только рациональные показатели r. Многие такие функции изучались ранее. Если r - натуральное число (r = n), то получаем функцию у = хⁿ. При n = 1; 2; 3 получаем графики прямой (n = 1), параболы (n = 2) и кубической параболы (n = 3). График степенной функции у = хⁿ в случае четного n (n = 4, 6, 8) похож на параболу (у = х²), а в случае нечетного n (n = 5, 7, 9, ...) - на кубическую параболу (у = х³).

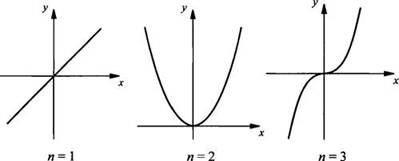
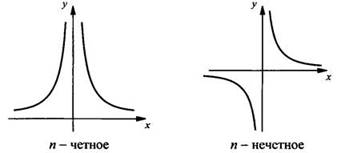
Если r = -n, то получаем степенную функцию у = х^-n или  Вид таких функций при четных и нечетных n представлен на рисунке.

При r = 0 имеем функцию у = х⁰ или у = 1 (где х ≠ 0). Графиком такой функции является горизонтальная прямая у = 1 с выколотой точкой х = 0 (х > 0).

Рассмотрим теперь степенные функции  с рациональными показатели степени. Их свойства и графики существенно зависят от показателя степени 

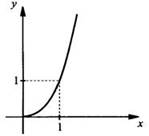
Свойства функции  для 

1. Область определения D(f) = [0; +∞).

2. Определенной четности не имеет.

3. Возрастает на промежутке [0; +∞).

4. Ограничена снизу и не ограничена сверху.

5. Наименьшее значение y_наим = 0, наибольшего значения не имеет.

6. Непрерывна.

7. Область значений E(f) = [0; +∞).

8. Выпукла вниз.

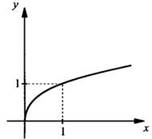
Свойства функции  для 

1. Область определения D(f) = [0; +∞).

2. Определенной четности не имеет.

3. Возрастает на промежутке [0; +∞).

4. Ограничена снизу и не ограничена сверху.

5. Наименьшее значение у_наим = 0, наибольшего значения не имеет.

6. Непрерывна.

7. Область значений E(f) = [0; +∞).

8. Выпукла вверх.

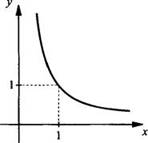
Свойства функции  для 

1. Область определения D(f) = (0; +∞).

2. Определенной четности не имеет.

3. Убывает на промежутке (0; +∞).

4. Ограничена снизу и не ограничена сверху.

5. Наименьшего и наибольшего значений не имеет.

6. Непрерывна.

7. Область значений E(f) = (0; +∞).

8. Выпукла вниз.

Наконец обсудим производную степенной функции.

Теорема (без доказательств). Если х > 0 и r - любое рациональное число, то производная степенной функции у = х^r вычисляется по формуле y' = rx^r-1.

Пример 1

Найдем производную функцию:

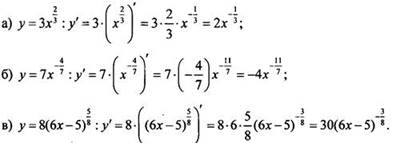
При этом было использовано правило дифференцирования 

Пример 2

Исследуем функцию  на монотонность и экстремумы и построим ее график.

1. Найдем производную данной функции: 

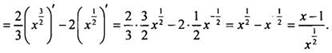
2. Функция существует при х ≥ 0, производная существует при х > 0. Поэтому критических точек у функции нет. Стационарную точку найдем из условия у' = 0 или  откуда х = 1.

3. Очевидно, что при х ∈ (0; 1], значение у' ≤ 0 и функция у(х) убывает на этом промежутке. При х ∈ [1; +∞) значение у' ≥ 0 и функция у(х) возрастает. В точке х = 1 функция у(х) имеет минимум 

4. График функции у(х) пересекает ось абсцисс в точке, которая является решением уравнения  или  откуда х = 0 или х = 3.

5. Построим график функции у(х).

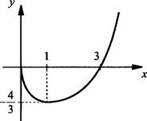
Пример 3

Найдем наименьшее и наибольшее значения функции  на:

а) отрезке [0; 27]; б) интервале (0; 27); в) отрезке [8; 27].

1. Найдем производную данной функции: 

2. Функция существует при х ≥ 0, производная существует при х > 0. Поэтому критических точек у функции нет. Стационарную точку найдем из условия у' = 0 или  откуда  и х = 1.

3. При х ∈ (0; 1] значение у' ≥ 0 и функция у(х) убывает на этом промежутке. При x ∈ [1; +∞) значение у’ = 0 и функция y(х) возрастает. В точке х = 1 функция у(х) имеет минимум 

а) Найдем значения функции на концах промежутка [0; 27]. у(0) = 0,  Точка минимума лежит на данном промежутке, и  Тогда наименьшее значение функции на отрезке  наибольшее значение 

б) Так как концы промежутка 0 и 27 интервалу (0; 27) не принадлежат, то функция у(х) наибольшего значения не имеет. Точка х = 1 лежит на данном интервале, и наименьшее значение функции 

в) На промежутке [8; 27] функция у(х) возрастает. Поэтому наименьшее значение функции  и наибольшее значение 

Пример 4

Напишем уравнение касательной к графику функции  в точке a = 1.

Напомним общий вид уравнения касательной: 

1. Найдем значение функции: 

2. Найдем производную функции: и ее значение f'(1) = 1.

3. Подставим значения f(a), f’(а) и а в уравнение касательной и получим: у = 1 + 1 ∙ (х - 1) или у = х.

IV. Контрольные вопросы

1. Определение степенной функции у = x^r.

2. Свойства функции  и ее график для:  

3. Производная степенной функции.

V. Задание на уроке

§ 38, № 3 (а); 7; 11; 12 (а, г); 15(6); 17; 20 (а, б); 26 (а, в); 27 (в, г); 28 (б); 30 (а, б); 31 (а); 32 (г); 33 (а); 39 (б).

VI. Задание на дом

§ 38, № 3 (б); 8; 10; 12 (б, в); 15 (в); 18; 21 (в, г); 26 (б, г); 27 (а, б); 28 (г); 30 (в, г); 31 (б); 32 (а); 33 (б); 39 (а).

VII. Подведение итогов урока