
Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год
Зачетная работа по теме Степени и корни. Степенные функции - Степени и корни. Степенные функции
Цель: проверка знаний учащихся по вариантам одинаковой сложности.
Ход уроков
I. Сообщение темы и цели уроков
II. Характеристика зачетной работы
Работа составлена в двух равноценных вариантах. По сравнению с контрольной работой увеличено количество заданий. Соответственно” У учащихся возрастает возможность выбора задач. Все задания разбиты на три блока А, В и С. Самые простые задачи находятся в части А, более сложные - в части В, еще сложнее - в части С. Каждая задача из А оценивается в 1 балл, из В - в 2 балла, из С — в 3 балла. Поэтому за правильное решение всех задач блока А можно получить 7 баллов, блока В - 8 баллов и блока С - 9 баллов (всего 24 балла). Оценка 3 ставится за 6 баллов, оценка 4 - за 10 баллов, оценка 5 - за 14 баллов.
Так как эта работа является зачетной, то в нее не включены принципиально новые задачи. Поэтому разбору заданий работы отдельного задания можно и не посвящать (решения задач могут быть вывешены на стенде). Для стендового размещения разбор вариантов приводится.
III. Варианты зачетной работы
Вариант 1
А
1.
Вычислите значение числового выражения ![]()
2.
Расположите числа ![]() в
порядке возрастания.
в
порядке возрастания.
3.
Найдите области определения и значений функции ![]()
4.
Постройте график функции ![]()
5.
Определите число решений системы уравнений ![]() Найдите
эти решения.
Найдите
эти решения.
6.
Упростите выражение ![]()
7.
Найдите производную функции ![]()
В
8.
Найдите значение выражения ![]()
9.
Упростите выражение ![]()
10.
Решите уравнение ![]()
11.
Постройте график функции ![]()
C
12.
Даны две функции: ![]() Докажите
тождество f(g(x)) = g(f(x)) и найдите значение выражения f(g(2)).
Докажите
тождество f(g(x)) = g(f(x)) и найдите значение выражения f(g(2)).
13.
Решите уравнение ![]()
14.
Прямая касается графика функции ![]() и
проходит через точку (-11/3; 0). Найдите координаты точки пересечения этой
прямой с осью ординат.
и
проходит через точку (-11/3; 0). Найдите координаты точки пересечения этой
прямой с осью ординат.
Вариант 2
А
1.
Вычислите значение числового выражения ![]()
2.
Расположите числа ![]() в
порядке возрастания.
в
порядке возрастания.
3.
Найдите области определения и значений функции ![]()
4.
Постройте график функции ![]()
5.
Определите число решений системы уравнений ![]() Найдите
эти решения.
Найдите
эти решения.
6.
Упростите выражение ![]()
7.
Найдите производную фикции ![]()
В
8.
Найдите значение выражения ![]()
9.
Упростите выражение ![]()
10.
Решите уравнение ![]()
11.
Постройте график функции ![]()
С
12.
Даны две функции: ![]() Докажите
тождество f(g(x)) = g(f(x)) и найдите значение выражения f(g(-2)).
Докажите
тождество f(g(x)) = g(f(x)) и найдите значение выражения f(g(-2)).
13.
Решите уравнение ![]()
14.
Прямая касается графика функции ![]() и
проходит через точку (-15/4; 0). Найдите координаты точки пересечения этой
прямой с осью ординат.
и
проходит через точку (-15/4; 0). Найдите координаты точки пересечения этой
прямой с осью ординат.
Ответы
Вариант 1
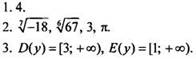
4. График построен.
5. Одно решение (1; 1).
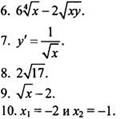
11. График построен.
Решения
12. Функции f(x) и g(x) взаимообратные. По свойству таких функций f(g(x)) = g(f(x)) = х Так как обычно такого свойства не помнят, то вычислим значения данных функций непосредственно:
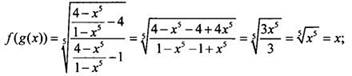
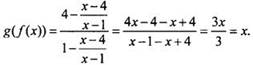 Таким
образом, тождество доказано и f(g(2)) = 2.
Таким
образом, тождество доказано и f(g(2)) = 2.
Ответ: тождество доказано, f(g(2)) = 2.
13.
Введем новые переменные ![]() Получаем
первое уравнение: a - b = 3. Возведем в куб переменные а и b: а3 =
х + 5 и b3 = х - 4. Вычтем эти выражения и получим второе
уравнение: а3 - b3 = 9, или (a - b)(a2 +
ab + b2) = 9, или a2 + ab + b2 = 3.
Имеем систему двух уравнений:
Получаем
первое уравнение: a - b = 3. Возведем в куб переменные а и b: а3 =
х + 5 и b3 = х - 4. Вычтем эти выражения и получим второе
уравнение: а3 - b3 = 9, или (a - b)(a2 +
ab + b2) = 9, или a2 + ab + b2 = 3.
Имеем систему двух уравнений: ![]() Из
первого уравнения выразим а = b + 3 и подставим во второе уравнение. Получаем
квадратное уравнение: (b + 3)2 + (b + 3)b + b2 =
3 или b2 + 3b + 2 = 0, корни которого b1 = -1 и
b2 = -2. Учтем, что х = b3 + 4 и найдем x1 =
3 и х2 = -4.
Из
первого уравнения выразим а = b + 3 и подставим во второе уравнение. Получаем
квадратное уравнение: (b + 3)2 + (b + 3)b + b2 =
3 или b2 + 3b + 2 = 0, корни которого b1 = -1 и
b2 = -2. Учтем, что х = b3 + 4 и найдем x1 =
3 и х2 = -4.
Ответ: x1 = 3 и х2 = -4.
14.
Напишем уравнение касательной. Найдем производную функцию ![]() и
получим:
и
получим: ![]()
![]() Предположим,
что касание происходит в точке х = а. Получаем уравнение касательной:
Предположим,
что касание происходит в точке х = а. Получаем уравнение касательной: ![]() или
или ![]() Для
нахождения величины а учтем, что касательная проходит через точку (-11/3; 0).
Получаем уравнение:
Для
нахождения величины а учтем, что касательная проходит через точку (-11/3; 0).
Получаем уравнение: 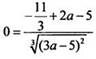 или
или ![]() откуда
а = 13/3. Тогда уравнение касательной имеет вид:
откуда
а = 13/3. Тогда уравнение касательной имеет вид: 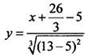 или
или 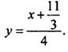 Подставим
значение х = 0 и найдем точку пересечения касательной с осью ординат: у =
11/12. Таким образом, координаты этой точки (0; 11/12).
Подставим
значение х = 0 и найдем точку пересечения касательной с осью ординат: у =
11/12. Таким образом, координаты этой точки (0; 11/12).
Ответ: (0; 11/12).
Ответы
Вариант 2
4. График построен.
5. Одно решение (1; 1).
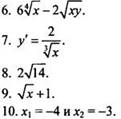
11. График построен.
Решения
12. Функции f(x) и g(x) взаимообратные. По свойству таких функций f(g(x)) = g(f(x)) = х. Так как обычно такого свойства не помнят, то вычислим значения данных функций непосредственно:
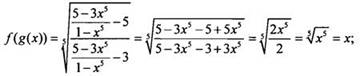
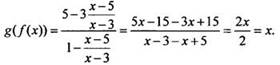 Таким
образом, тождество доказано и f(g(-2)) = -2.
Таким
образом, тождество доказано и f(g(-2)) = -2.
Ответ: тождество доказано, f(g(-2)) = -2.
13.
Введем новые переменные ![]() Получаем
первое уравнение: a - b = 1. Возведем в куб переменные а и b: а2 =
х - 3 и b2 = х - 10. Вычтем эти выражения и получим второе
уравнение: а3 - b3 = 7, или
Получаем
первое уравнение: a - b = 1. Возведем в куб переменные а и b: а2 =
х - 3 и b2 = х - 10. Вычтем эти выражения и получим второе
уравнение: а3 - b3 = 7, или ![]() или
a2 + ab + b2 = 7. Имеем систему двух
уравнений:
или
a2 + ab + b2 = 7. Имеем систему двух
уравнений: ![]() Из
первого уравнения выразим а = b + 1 и подставим во второе уравнение. Получаем
квадратное уравнение:
Из
первого уравнения выразим а = b + 1 и подставим во второе уравнение. Получаем
квадратное уравнение: ![]() или
b2 + b - 2 = 0, корни которого b1 = -2 и b2 =
1. Учтем, что х = b3 + 10, и найдем x1 = 2 и х2 =
11.
или
b2 + b - 2 = 0, корни которого b1 = -2 и b2 =
1. Учтем, что х = b3 + 10, и найдем x1 = 2 и х2 =
11.
Ответ: x1 = 2 и х2 = 11.
14.
Напишем уравнение касательной. Найдем производную функцию ![]() и
получим:
и
получим: ![]()
![]() Предположим,
что касание происходит в точке х = а. Получаем уравнение касательной:
Предположим,
что касание происходит в точке х = а. Получаем уравнение касательной: ![]() или
или ![]() Для
нахождения величины а учтем, что касательная проходит через точку (-19/4; 0).
Получаем уравнение:
Для
нахождения величины а учтем, что касательная проходит через точку (-19/4; 0).
Получаем уравнение: ![]() или
0 = -19 + 8а + 9, откуда а = 5/4. Тогда уравнение касательной имеет вид:
или
0 = -19 + 8а + 9, откуда а = 5/4. Тогда уравнение касательной имеет вид: ![]() или
или ![]() Подставим
значение х = 0 и найдем точку пересечения касательной с осью ординат: у = 3/4.
Таким образом, координаты этой точки (0; 3/4).
Подставим
значение х = 0 и найдем точку пересечения касательной с осью ординат: у = 3/4.
Таким образом, координаты этой точки (0; 3/4).
Ответ: (0; 3/4).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.