
Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год
Решение показательных уравнений и неравенств - Показательная и логарифмическая функции
Цели: систематизировать виды показательных выражений; рассмотреть способы решений уравнений, систем уравнений, неравенств.
Ход уроков
I. Сообщение темы и целей уроков
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (тест).
Вариант 1
1. Найдите значение выражения
Ответы: а) 1; б) 25; в) 5; г) 1/5.
2. Упростите выражение
Ответы:
3. Найдите область значений функции
Ответы: ![]()
Вариант 2
1.
Найдите значение выражения ![]()
Ответы: а) 1; б) 4; в) 2; г) 1/4.
2.
Упростите выражение ![]()
Ответы: ![]()
3.
Найдите область значений функции ![]()
Ответы: ![]()
III. Изучение нового материала
Показательные уравнения
Показательным уравнением называется уравнение, в котором неизвестное л: входит только в показатели степени при некоторых постоянных основаниях.
Пример 1
а)
Уравнение ![]() показательное;
показательное;
б)
уравнение ![]() не
является показательным. Рассмотрим систематику показательных выражений и
способы решения уравнений. Так как показательная функция ax монотонна
и ее область значений (0; ∞), то простейшее показательное уравнение ax =
b имеет единственный корень при b > 0. Именно к виду ax = b
надо сводить более сложные уравнения.
не
является показательным. Рассмотрим систематику показательных выражений и
способы решения уравнений. Так как показательная функция ax монотонна
и ее область значений (0; ∞), то простейшее показательное уравнение ax =
b имеет единственный корень при b > 0. Именно к виду ax = b
надо сводить более сложные уравнения.
1. Простейшие уравнения
Пример 2
Решим
уравнение ![]()
Правую
часть уравнения представим в виде степени числа 4 и получим: ![]() Так
как равны степени числа 4, то равны и показатели степеней. Имеем квадратное
уравнение х2 + 3х = -2 или х2 + 3х + 2 = 0.
Корни этого уравнения x1 = -1 и х2 = -2
являются и решениями данного уравнения.
Так
как равны степени числа 4, то равны и показатели степеней. Имеем квадратное
уравнение х2 + 3х = -2 или х2 + 3х + 2 = 0.
Корни этого уравнения x1 = -1 и х2 = -2
являются и решениями данного уравнения.
2. Уравнения, решаемые его преобразованиями
Пример 3
Решим
уравнение ![]()
Так
как все слагаемые в левой части уравнения имеют вид 5х+а (где а
- некоторое число), то вынесем общий множитель 5х за скобки.
Получаем: ![]() или
5х ∙ 100 = 4. Разделим обе части уравнения на число 100.
Имеем:
или
5х ∙ 100 = 4. Разделим обе части уравнения на число 100.
Имеем: ![]() или
5х = 5-2. Так как равны степени числа 5, то равны и
показатели степеней. Тогда находим единственный корень данного уравнения х =
-2.
или
5х = 5-2. Так как равны степени числа 5, то равны и
показатели степеней. Тогда находим единственный корень данного уравнения х =
-2.
Вынесение общего множителя за скобки можно использовать и при решении уравнений, содержащих степени с двумя разными основаниями.
Пример 4
Решим
уравнение ![]()
В
данное уравнение входят числа 2 и 3 в различных степенях. Поэтому сгруппируем
члены уравнения, содержащие степени числа 3, в левой части, а члены, содержащие
степени числа 2, - в правой. Получаем: ![]() В
левой части вынесем за скобки общий множитель
В
левой части вынесем за скобки общий множитель ![]() в
правой - общий множитель
в
правой - общий множитель ![]() Имеем:
Имеем: ![]() или
или ![]() или
или ![]() Разделим
обе части этого уравнения на правую часть (очевидно, она не равна нулю):
Разделим
обе части этого уравнения на правую часть (очевидно, она не равна нулю): ![]() или
или 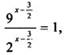 или
или ![]() Так
как равны степени числа 9/2, то равны и показатели степеней:
Так
как равны степени числа 9/2, то равны и показатели степеней: ![]() откуда
х = 3/2.
откуда
х = 3/2.
3. Уравнения, решаемые разложением на множители
Одним из наиболее распространенных преобразований является разложение уравнения на множители. В частности, оно используется при различных основаниях степеней.
Пример 5
Решим
уравнение ![]()
Число
5400 разложим на простые множители: ![]() Тогда
уравнение имеет вид:
Тогда
уравнение имеет вид: ![]() Разделим
обе части уравнения на его правую часть. Получаем или
Разделим
обе части уравнения на его правую часть. Получаем или ![]() или
или ![]() или
или ![]() тогда
x - 2 = 0 и х = 2.
тогда
x - 2 = 0 и х = 2.
Разложение на множители также используется и в уравнениях, содержащих, помимо показательных функций, другие функции.
Пример 6
Решим
уравнение ![]()
Перенесем
все члены уравнения в левую часть, сгруппируем их и вынесем общие множители за
скобки. Имеем: ![]() или
или ![]() или
или ![]() или
или ![]() Так
как произведение двух множителей равно нулю, то один из них равен нулю.
Получаем два уравнения:
Так
как произведение двух множителей равно нулю, то один из них равен нулю.
Получаем два уравнения:
а) 5х - 1 = 0 или 5х = 50, откуда х = 0;
б)
2 sin x - 1 = 0 или sin x = 1/2, тогда ![]()
![]() где
n ∈ Z.
где
n ∈ Z.
4. Уравнения, решаемые с помощью замены неизвестной
Как и в уравнениях других видов, в случае показательных уравнений часто используется замена неизвестной.
Пример 7
Решим
уравнение ![]()
Запишем
данное уравнение в виде ![]() и
введем новую неизвестную t = 3х > 0. Получаем
уравнение
и
введем новую неизвестную t = 3х > 0. Получаем
уравнение ![]() или
3t2 – 8t - 3 = 0. Корни этого квадратного уравнения t1 =
3 и t2 = -1/3 (не подходит, т. к. t > 0). Получаем
простейшее показательное уравнение 3х = 3, решение которого х =
1.
или
3t2 – 8t - 3 = 0. Корни этого квадратного уравнения t1 =
3 и t2 = -1/3 (не подходит, т. к. t > 0). Получаем
простейшее показательное уравнение 3х = 3, решение которого х =
1.
Пример 8
Решим
уравнение ![]()
Учтем
основное тригонометрическое тождество ![]() тогда
тогда ![]() Уравнение
теперь имеет вид:
Уравнение
теперь имеет вид: ![]() Введем
новую неизвестную
Введем
новую неизвестную ![]() и
получим уравнение
и
получим уравнение ![]() или
t2 - 6t + 8 = 0. Корни этого квадратного уравнения t1 =
2 и t2 = 4. Вернемся к старой неизвестной х и получим два
уравнения:
или
t2 - 6t + 8 = 0. Корни этого квадратного уравнения t1 =
2 и t2 = 4. Вернемся к старой неизвестной х и получим два
уравнения:
а) ![]() тогда
sin2х = 1 или sinx = ±1. Решение этих уравнений
тогда
sin2х = 1 или sinx = ±1. Решение этих уравнений ![]() где
n ∈ Z.
где
n ∈ Z.
б) ![]() откуда
sin2х = 2. Это уравнение решений не имеет, т. к. функция синус
ограниченна: sinx ≤ 1 и sin2x ≤ 1 - при всех х.
откуда
sin2х = 2. Это уравнение решений не имеет, т. к. функция синус
ограниченна: sinx ≤ 1 и sin2x ≤ 1 - при всех х.
В ряде случаев для решения показательного уравнения приходится вводить две новые переменные и сводить уравнение к однородному.
Пример 9
Решим
уравнение ![]()
Запишем
данное уравнение в виде ![]() и
введем две новые неизвестные
и
введем две новые неизвестные ![]() Получаем
однородное уравнение а2 + b2 - 2ab = 0 или (а -
b)2 = 0, откуда а - b = 0 или а = b. Вернемся к старой
неизвестной х. Получаем уравнение
Получаем
однородное уравнение а2 + b2 - 2ab = 0 или (а -
b)2 = 0, откуда а - b = 0 или а = b. Вернемся к старой
неизвестной х. Получаем уравнение ![]() Так
как равны степени числа 3, то равны и показатели степеней. Имеем квадратное
уравнение: х + 6 = х2 или 0 = х2 - х - 6, корни
которого x1 = -2 и х2 = 3.
Так
как равны степени числа 3, то равны и показатели степеней. Имеем квадратное
уравнение: х + 6 = х2 или 0 = х2 - х - 6, корни
которого x1 = -2 и х2 = 3.
5. Уравнения, решаемые с помощью его специфики
Название этого типа уравнений достаточно условно: при решении любого уравнения в той или иной степени учитывается его специфичность. Поэтому рассмотрим несколько примеров.
Пример 10
Решим
уравнение ![]()
Легко
угадать корень уравнения: х = 2. Действительно, при подстановке получаем верное
равенство: 72 + 242 = 252. Покажем,
что других решений уравнение не имеет. Разделим все члены уравнения на его
правую часть и получим: ![]() Очевидно,
что функции
Очевидно,
что функции ![]() убывающие,
т. к. их основания меньше 1.
убывающие,
т. к. их основания меньше 1.
Сумма этих функций также является функцией убывающей. Поэтому по теореме о корне данное уравнение имеет единственное решение.
Пример 11
Решим
уравнение ![]()
Данное уравнение не является показательным, т. к. неизвестная входит и в основание, и в показатель степени.
При
решении уравнений вида ![]() необходимо
помнить, что число х0 будет корнем этого уравнения, если имеет
место один из следующих четырех случаев:
необходимо
помнить, что число х0 будет корнем этого уравнения, если имеет
место один из следующих четырех случаев:
а) f(х0) = -1, а числа g(x0) и h(x0) - целые числа одинаковой четности;
б) f(х0) = 0, а числа g(x0) и h(х0) положительные;
в) f(х0) = 1, а функции g(x) и h(х) определены при х = х0;
г)
g(x0) = h(х0), а функции ![]() определены
при х = х0.
определены
при х = х0.
Рассмотрим все перечисленные выше случаи:
а) х - 2 = -1, т. е. х= 1. При этом х2 + 2х = 12 + 2 ∙ 1 = 3 и 11х - 20 = 11 ∙ 1 - 20 = -9, т. е. числа 3 и -9 - целые числа одинаковой четности и числа (-1)3 и (-1)-9 существуют и равны - 1;
б) х - 2 = 0, т. е. х = 2. При этом х2 + 2х = 22 + 2 ∙ 2 = 8 и 11х - 20 = 11 ∙ 2 - 20 = 2, т. е. числа 8 и 2 положительные и числа 08 и 02 существуют и равны;
в) х - 2 = 1, т. е. х = 3. При этом х2 + 2х = 32 + 2 ∙ 3 = 15 и 11х - 20 = 11 ∙ 3 - 20 = 13, т. е. функции х2 + 2х и 11х - 20 при х = 3 определены. Заметим, что числа 115 и 113 равны друг другу и равны 1;
г) х2 + 2х = 11х - 20 или х2 - 9х + 20 = 0, т. е. x1 = 4 и х2 = 5.
При
х = 4 функции, входящие в уравнение, определены: ![]() и
и ![]() -
и их значения равны друг другу и равны 224. При х = 5 функции также
определены:
-
и их значения равны друг другу и равны 224. При х = 5 функции также
определены: ![]() - и
их значения равны 335.
- и
их значения равны 335.
Итак, уравнение имеет пять корней: x1 = 1, х2 = 2, х3 = 3, x4 = 4, x5 = 5.
Обратимся теперь к задачам, для решения которых необходимо найти области изменения функций, входящих в уравнение.
Пример 12
Решим
уравнение ![]()
Найдем
области изменения функций ![]() Первая
функция показательная с основанием 2 > 1, и так как |х - 1| ≥ 0, то у
≥ 20 = 1. Вторая функция - парабола, направленная ветвями
вниз, проходящая через точки х = 0 и х = 2. Максимум этой параболы достигается
при х = 1 и равен у = 2 ∙ 1 - 12 = 1. При остальных х у
≤ 1. Таким образом, значения этих двух функций совпадают только при х = 1
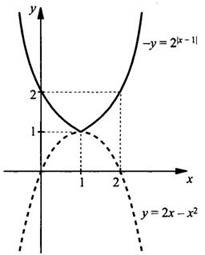
и равны 1. Итак, х = 1 - корень уравнения. Полезно решение в простейших
случаях, например в этом, иллюстрировать графическим решением (см. рисунок).
Первая
функция показательная с основанием 2 > 1, и так как |х - 1| ≥ 0, то у
≥ 20 = 1. Вторая функция - парабола, направленная ветвями
вниз, проходящая через точки х = 0 и х = 2. Максимум этой параболы достигается
при х = 1 и равен у = 2 ∙ 1 - 12 = 1. При остальных х у
≤ 1. Таким образом, значения этих двух функций совпадают только при х = 1
и равны 1. Итак, х = 1 - корень уравнения. Полезно решение в простейших
случаях, например в этом, иллюстрировать графическим решением (см. рисунок).
6. Уравнения, решаемые графически
При решении уравнений, содержащих показательные и другие функции, достаточно часто используется графический способ.
Пример 13
Решим
уравнение ![]()
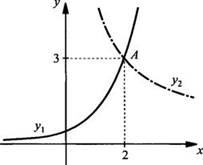
Построим
графики функций ![]() Видно,
что графики этих функций пересекаются в единственной точке А, абсцисса которой
х = 2 является решением данного уравнения.
Видно,
что графики этих функций пересекаются в единственной точке А, абсцисса которой
х = 2 является решением данного уравнения.
Показательные неравенства
При решении простейших показательных неравенствaf(x) v b используется монотонность показательной функции: при 0 < a < 1 функция убывающая, при a > 1 - возрастающая. Поэтому при рассмотрении показателей степеней в первом случае знак неравенства меняется на противоположный, во втором - сохраняется.
Пример 14
Решим
неравенство ![]()
Запишем
неравенство в виде ![]() Так
как основание 2 показательной функции больше единицы (показательная функция
возрастающая), то показатели степеней связаны неравенством того же знака:
Так
как основание 2 показательной функции больше единицы (показательная функция
возрастающая), то показатели степеней связаны неравенством того же знака: ![]() или
х2 - 14,5 + 30 < 0. Решение этого квадратного неравенства х ∈ (2,5; 12).
или
х2 - 14,5 + 30 < 0. Решение этого квадратного неравенства х ∈ (2,5; 12).
Пример 15
Решим
неравенство ![]() Так
как основание 0,8 показательной функции меньше 1 (показательная функция
убывающая), то показатели степеней связаны неравенством противоположного знака:
х3 - 3х + 4 ≤ 2 или х3 - 3х + 2 ≤
0. Разложим левую часть на множители: (х - 1)2(х + 2) ≤ 0 и
решим это кубическое неравенство методом интервалов. Получаем решение: х ∈ (-∞;
-2] U {1}.
Так
как основание 0,8 показательной функции меньше 1 (показательная функция
убывающая), то показатели степеней связаны неравенством противоположного знака:
х3 - 3х + 4 ≤ 2 или х3 - 3х + 2 ≤
0. Разложим левую часть на множители: (х - 1)2(х + 2) ≤ 0 и
решим это кубическое неравенство методом интервалов. Получаем решение: х ∈ (-∞;
-2] U {1}.
![]()
При решении более сложных неравенств используются те же приемы, что и при решении аналогичных уравнений.
Пример 16
Решим
неравенство ![]()
Введем
новую неизвестную t = 3х > 0 и получим рациональное
неравенство: ![]() или
или ![]() или
или ![]() Учтем,
что t > 0, и решим это неравенство методом интервалов. Получаем: t ∈ (1/3; 3].
Вернемся к старой неизвестной. Имеем двойное неравенство 3-1 <
3х ≤ 3. Так как основание 3 степеней больше единицы, то
показатели степеней связаны неравенствами того же знака: -1 < х ≤ 1
или x ∈ (-1; 1].
Учтем,
что t > 0, и решим это неравенство методом интервалов. Получаем: t ∈ (1/3; 3].
Вернемся к старой неизвестной. Имеем двойное неравенство 3-1 <
3х ≤ 3. Так как основание 3 степеней больше единицы, то
показатели степеней связаны неравенствами того же знака: -1 < х ≤ 1
или x ∈ (-1; 1].
Пример 17
Решим
неравенство ![]()
ОДЗ
неравенства х ∈ (2; ∞).Запишем неравенство в виде ![]() и
найдем корни соответствующего уравнения: x1 = 3 и х2 =
4. Решая методом интервалов это неравенство с учетом ОДЗ, получаем: х ∈ (2; 3] U
[4; ∞).
и
найдем корни соответствующего уравнения: x1 = 3 и х2 =
4. Решая методом интервалов это неравенство с учетом ОДЗ, получаем: х ∈ (2; 3] U
[4; ∞).
![]()
Системы показательных уравнений
При решении систем показательных уравнений применяются те же способы, что и для решения показательных уравнений. Достаточно часто системы непосредственно сводятся к системам алгебраических уравнений.
Пример 18
Решим
систему уравнений ![]()
Запишем
данную систему уравнений в виде ![]() Получаем
систему алгебраических уравнений
Получаем
систему алгебраических уравнений ![]() Из
второго уравнения выразим у = 2х - 4 и подставим в первое. Имеем:
Из
второго уравнения выразим у = 2х - 4 и подставим в первое. Имеем: ![]() или
5х2 – 2x - 3 = 0. Корни этого уравнения x1 = 1
и х2 = -3/5. Найдем соответствующие значения у1 =
-2 и
или
5х2 – 2x - 3 = 0. Корни этого уравнения x1 = 1
и х2 = -3/5. Найдем соответствующие значения у1 =
-2 и ![]() Итак,
система уравнений имеет два решения: (1; -2) и
Итак,
система уравнений имеет два решения: (1; -2) и ![]()
Разумеется, при решении систем уравнений широко используется замена неизвестных.
Пример 19
Решим
систему уравнений ![]()
Из
второго уравнения найдем: 2х - у = 3, откуда y = 2х - 3. Подставим это
соотношение в первое уравнение и получим: ![]() или
или ![]() Введем
новую неизвестную: t = 3х > 0. Имеем квадратное
уравнение
Введем
новую неизвестную: t = 3х > 0. Имеем квадратное
уравнение ![]() или
2t2 + 27t - 405 = 0, корни которого t1 = 0 и t2 =
-22,5 (не подходит, т. е. t > 0). Возвращаясь к старым неизвестным, получаем
уравнение 3х = 9, находим: х = 2 и у = 1.
или
2t2 + 27t - 405 = 0, корни которого t1 = 0 и t2 =
-22,5 (не подходит, т. е. t > 0). Возвращаясь к старым неизвестным, получаем
уравнение 3х = 9, находим: х = 2 и у = 1.
Пример 20
Решим
систему уравнений ![]()
Систему
уравнений запишем в виде 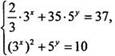 и
введем новые переменные a = 3х и b = 5y (при
этом a, b > 0). Получаем систему алгебраических уравнений
и
введем новые переменные a = 3х и b = 5y (при
этом a, b > 0). Получаем систему алгебраических уравнений 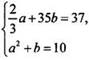 или
или ![]() Из
второго уравнения выразим b = 10 - а2 и подставим в первое.
Имеем: 2а + 105(10 - а2) = 111 или 0 = 105а2 - 2а -
939. Корни этого квадратного уравнения а1 = 3 и а2 =
-313/105 (не подходит, т. к. а > 0). Найдем b = 10 - 32 = 1.
Вернемся к старым неизвестным. Получаем систему простейших показательных
уравнений
Из
второго уравнения выразим b = 10 - а2 и подставим в первое.
Имеем: 2а + 105(10 - а2) = 111 или 0 = 105а2 - 2а -
939. Корни этого квадратного уравнения а1 = 3 и а2 =
-313/105 (не подходит, т. к. а > 0). Найдем b = 10 - 32 = 1.
Вернемся к старым неизвестным. Получаем систему простейших показательных
уравнений ![]() откуда
х = 1 и у = 0.
откуда
х = 1 и у = 0.
IV. Задание на уроках
§ 40, № 7 (а, б); 12 (в, г); 13 (а, в); 15 (б, г); 17 (а, б); 18 (а); 21 (б); 23 (а, б); 26 (в, г); 28 (б); 29 (а); 34 (а, б); 39 (а, в); 41 (б, г); 45 (а, в); 49 (а, б); 50 (a).
V. Задание на дом
§ 40, № 7 (в, г); 12 (а, б); 13 (б, г); 15 (а, в); 17 (в, г); 18 (б); 21 (а); 23 (в, г); 26 (а, б); 28 (г); 29 (б); 34 (в, г); 39 (б, г); 41 (а, в); 45 (б, г); 49 (в, г); 50 (б).
VI. Творческие задания
1. Решите показательное уравнение:

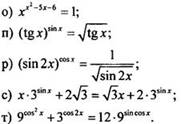
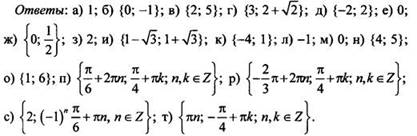
2. Решите показательное неравенство:
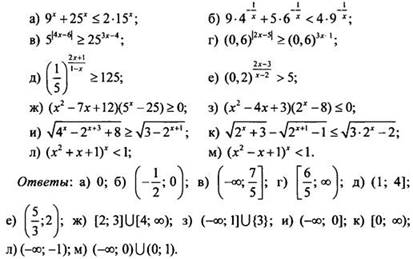
3. Решите систему показательных уравнений:
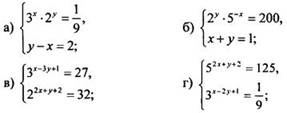
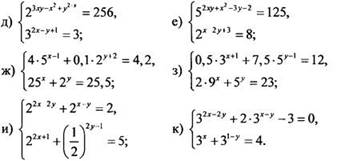
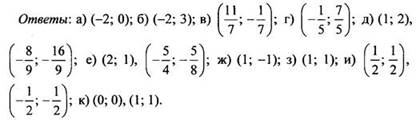
VII. Подведение итогов уроков
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.