алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Функция y = log_ax, ее свойства и график - Показательная и логарифмическая функции

Цель: рассмотреть логарифмическую функцию, ее свойства и график.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Вычислите: 

2. Решите уравнение: 

Вариант 2

1. Вычислите: 

2. Решите уравнение: 

III. Изучение нового материала

Как следует из предыдущего материала, показательная функция у = a^x (где a > 0 и а ≠ 1) монотонна, а значит, обратима. Выразим из этого равенства х = log_aу. Поменяем местами х и у и получим: у = log_ax. Таким образом, функции у = a^x и у = log_ax являются взаимообратными. Функцию, заданную формулой у = log_ax (где a > 0 и а ≠ 1), называют логарифмической функцией с основанием а.

Графики показательной и логарифмической функций, имеющие одинаковое основание а (как и любых взаимообратных функций) симметричны относительной прямой у = х. На рисунке приведены графики показательной и логарифмической функций, например, для случая а > 1.

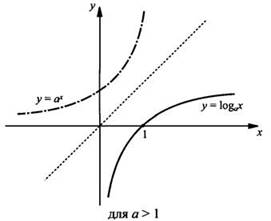
Приведем графики логарифмических функций у = log_ax для оснований 0 < а < 1 и а > 1.

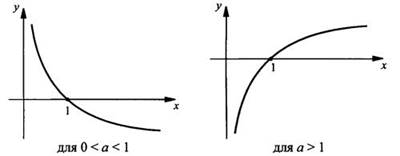
Исходя из приведенных графиков, перечислим основные свойства логарифмической функции.

1) Область определения функции D(f) = (0; +∞).

2) Функция определенной четности не имеет.

3) Функция убывающая при 0 < a < 1 и возрастающая при a > 1.

4) Функция не ограничена.

5) Функция не имеет ни наименьшего, ни наибольшего значений.

6) Функция непрерывна.

7) Область значений функции E(f) = (-∞; +∞).

8) Функция выпукла вниз при 0 < a < 1 и выпукла вверх при a > 1.

Рассмотрим примеры использования свойств логарифмической функции.

Пример 1

Найдем область определения функции у = log₂(-x² + 2х + 3).

Область определения логарифмической функции - множество всех положительных чисел R₊. Поэтому данная функция определена при всех х, для которых выполнено неравенство -х² + 2х + 3 > 0 или х² - 2х – 3 < 0. Решение этого квадратного неравенства х ∈ (-1; 3). Итак, область определения данной функции D(y) = (-1; 3).

Пример 2

Найдем область определения функции 

Область определения данной функции задается неравенством  Запишем его в виде  Так как основание логарифма 0,3 меньше единицы, то логарифмическая функция убывающая. Поэтому полученное неравенство равносильно двойному линейному неравенству 0 < 2х - 1 ≤ 1 или 1 < 2х ≤ 2, решение которого х ∈ (1/2; 1). Следовательно, область определения данной функции D(y) = (1/2; 1).

Пример 3

Найдем область значений функции 

Как и в примере 1, область определения данной функции D(y) = (-1; 3). Рассмотрим вспомогательную функцию z(x) = -х² + 2х + 3. Ее графиком является парабола, направленная ветвями вниз с вершиной в точке с координатами х = 1 и z = 4. При изменении х на промежутке (-1; 3) значения z ∈ (0; 4]. Функция  является убывающей, т. к. основание 1/2 логарифма меньше единицы. Поэтому значения y меняются от +∞ до  Итак, область значений данной функции Е(у) = [-2; +∞).

Пример 4

Установить четность (или нечетность) функции 

Сначала найдем область определения функции. Она задается неравенством xsinx > 0. При х > 0 получаем: sinx > 0. Решение этого неравенства  где n ∈ Z и n ≥ 0. При x < 0 sinx < 0. Решение такого неравенства  где k ∈ Z и k ≤ 0. Построив эти промежутки на числовой оси, легко увидеть, что область определения функции является симметричным множеством.

Теперь найдем  Так как выполнено равенство у(-х) = у(х), то по определению функция y(х) четная.

Достаточно часто встречаются задачи, связанные с построением графиков логарифмических функций. Для их построения используют те же приемы, что и для функций других видов. В ряде случаев функцию предварительно необходимо преобразовать.

Пример 5

Построим график функции:  

а) Учтем, что х - 1 > 0, т. е. х > 1. Выполним очевидные преобразования: (при условии х > 1).

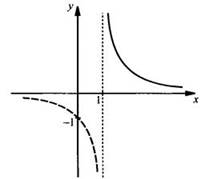
б) Очевидно, что этот график легко построить, используя схему: 

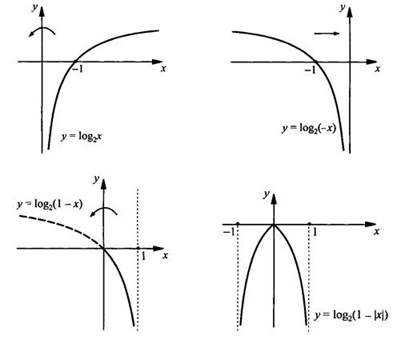
в) Несмотря на устрашающий вид функции у, график ее очень простой. D(y) функции задается условием  т. е.  Отсюда cosx = ±1 или x = πn, n ∈ Z. В этих точках у = 0.

Свойства монотонности логарифмической функции используются для сравнения чисел.

Пример 6

Сравним числа:  

а) Логарифмическая функция с основанием большим единицы является возрастающей, т. е. большему значению аргумента соответствует большее значение функции. Так как 7 < 8, то и log₅7 < log₅8, т. е. второе число больше.

б) Логарифмическая функция с основанием меньше единицы убывает в области определения, т. е. большему значению аргумента соответствует меньшее значение функции. Так как 7 < 8, то  т. е. первое число больше.

в) Оценим данные числа. Учтем, что основания логарифмов больше единицы. Так как 23 < 25, то log₅23 < log₅25 = 2. Учтем, что 39 > 36, и тогда log₆39 > log₆36 = 2. Итак, первое число меньше 2, а второе число больше 2. Поэтому log₅23 < log₆39, т. е. второе число больше.

IV. Контрольные вопросы

1. Дайте определение логарифмической функции.

2. Приведите графики логарифмической функции.

3. Перечислите основные свойства логарифмической функции (фронтальный опрос).

V. Задание на уроках

§ 42, № 1 (а, б); 3 (в, г); 5 (а); 6 (а, б); 8 (в, г); 9 (а); 10 (б); 11 (а, б); 14 (в, г); 17 (а, б); 19 (в, г); 22 (а); 23 (б); 25 (б).

VI. Задание на дом

§ 42, № 1 (в, г); 3 (а, б); 5 (б); 6 (в, г); 8 (а, б); 9 (б); 10 (а); 11 (в, г); 14 (а, б); 17 (в, г); 19 (а, б); 22 (б); 23 (в).

VII. Творческие задания

Постройте графики функций, уравнений, неравенств:

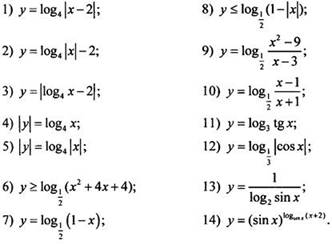
VIII. Подведение итогов уроков