
Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год
Логарифмические неравенства - Показательная и логарифмическая функции
Цель: рассмотреть особенности решения логарифмических неравенств.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Решите уравнение:
![]()
2. Решите систему уравнений:
![]()
Вариант 2
1. Решите уравнение:
![]()
2. Решите систему уравнений:
![]()
III. Изучение нового материала
При решении простейших логарифмических неравенств loga х v b необходимо учитывать монотонность логарифмической функции loga х: при 0 < a < 1 эта функция убывает, при a > 1 возрастает.
Пример 1
Решим неравенство log2 (x - 13) ≤ 3.
ОДЗ
неравенства задается условием х - 13 > 0. Запишем данное неравенство в
виде ![]() Так
как основание логарифмов 2 больше единицы, то логарифмическая функция
возрастающая и аргументы логарифмов связаны неравенством того же знака: х - 13
≤ 8. С учетом ОДЗ получаем, что данное неравенство равносильно двойному
линейному неравенству 0 < х - 13 ≤ 8, решение которого х ∈ (13; 21].
Так
как основание логарифмов 2 больше единицы, то логарифмическая функция
возрастающая и аргументы логарифмов связаны неравенством того же знака: х - 13
≤ 8. С учетом ОДЗ получаем, что данное неравенство равносильно двойному
линейному неравенству 0 < х - 13 ≤ 8, решение которого х ∈ (13; 21].
Пример 2
Решим
неравенство ![]()
ОДЗ
неравенства определяется условием 3х - 2 > 0. Так как основание логарифмов 2
меньше единицы, то логарифмическая функция убывающая и аргументы логарифмов
связаны неравенством противоположного знака, т. е. 3х - 2 > 7. С учетом ОДЗ
получаем, что данное неравенство равносильно системе неравенств ![]() Так
как второе неравенство более жесткое, чем первое, то полученная система (в свою
очередь) равносильна второму неравенству 3х - 2 > 7, решение которого х ∈ (3;
∞).
Так
как второе неравенство более жесткое, чем первое, то полученная система (в свою
очередь) равносильна второму неравенству 3х - 2 > 7, решение которого х ∈ (3;
∞).
Такие же соображения используются и при решении более сложных неравенств.
Пример 3
Решим
неравенство ![]()
Учтем,
что основание логарифма 1/2 меньше единицы, ОДЗ неравенства и ![]() Тогда
данное неравенство равносильно двойному неравенству
Тогда
данное неравенство равносильно двойному неравенству ![]() Запишем
это неравенство в виде системы неравенств и решим ее методом интервалов.
Получаем:
Запишем
это неравенство в виде системы неравенств и решим ее методом интервалов.
Получаем: 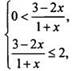 или
или 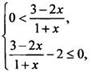 или
или 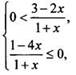 откуда
откуда 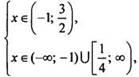 тогда
тогда ![]() Итак,
решение данного неравенства
Итак,
решение данного неравенства ![]()
Пример 4
Решим
неравенство ![]()
ОДЗ
неравенства: х ∈ (0; +∞). Возьмем от обеих частей неравенства логарифм по
основанию 10. При этом знак неравенства не изменится, т. к. основание логарифма
больше 1: ![]() Введем
замену у = lgx и придем к неравенству третьей степени
Введем
замену у = lgx и придем к неравенству третьей степени ![]() или
или ![]() которое
легко решается разложением на множители
которое
легко решается разложением на множители ![]() или
у - 3 > 0, откуда у > 3. Получаем простейшее логарифмическое неравенство
lgx > 3, откуда х > 103 = 1000. Итак, решение неравенства
х ∈ (1000; +∞).
или
у - 3 > 0, откуда у > 3. Получаем простейшее логарифмическое неравенство
lgx > 3, откуда х > 103 = 1000. Итак, решение неравенства
х ∈ (1000; +∞).
В случае, если в основание показательной или логарифмической функции входит неизвестная величина х, то, естественно, необходимо рассмотреть ситуации, когда это основание принадлежит промежутку (0; 1) и когда принадлежит промежутку (1; +∞).
Пример 5
Решим
неравенство ![]()
ОДЗ
неравенства определяется условиями 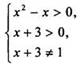 или
или 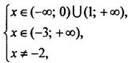 откуда
х ∈ (-3; - 2) U (-2; 0) U (1; +∞).
откуда
х ∈ (-3; - 2) U (-2; 0) U (1; +∞).
а)
При 0 < х + 3 < 1, т. е. х ∈ (-3; -2),
имеем: ![]() откуда
х2 - х > х + 3, так как при таком основании логарифмическая
функция убывающая. Решив это неравенство, найдем: х ∈ (-∞;
-1) U (3; +∞). Однако необходимо учесть ограничения на х (х ∈ (-3; -
2)). Тогда получаем х ∈ (-3; - 2).
откуда
х2 - х > х + 3, так как при таком основании логарифмическая
функция убывающая. Решив это неравенство, найдем: х ∈ (-∞;
-1) U (3; +∞). Однако необходимо учесть ограничения на х (х ∈ (-3; -
2)). Тогда получаем х ∈ (-3; - 2).
б)
При х + 3 > 1, т.е. х ∈ (-2; +∞), а с учетом ОДЗ х ∈ (-2; 0) U
(1; +∞), имеем: ![]() откуда
х2 – х < х + 3, так как при основании большем 1
логарифмическая функция возрастающая. Решив это неравенство, найдем х ∈ (-1; 3). С
учетом ограничений на х получаем: х ∈ (-1; 0) U
(1; 3).
откуда
х2 – х < х + 3, так как при основании большем 1
логарифмическая функция возрастающая. Решив это неравенство, найдем х ∈ (-1; 3). С
учетом ограничений на х получаем: х ∈ (-1; 0) U
(1; 3).
Объединяя первый и второй случаи, получаем решение неравенства: х ∈ (-3; -2) U (-1; 0) U (1; 3).
Разумеется, при решении логарифмических неравенств (как и других неравенств) очень эффективен метод интервалов.
Пример 6
Решим
неравенство ![]()
ОДЗ
неравенства задается условиями ![]()
Решение
этой системы линейных неравенств х > -0,5. Найдем значения х, при которых
числитель и знаменатель данной дроби обращаются в нуль. Решив уравнение log2(x
+ 3) - 2 = 0, найдем х = 1. Решая уравнение log5(2x + 1) - 1 = 0,
получим х = 2. Нанесем эти точки на координатную ось. Для любого значения х,
входящего в ОДЗ, определим знак данной дроби. Например, для х = 10
получаем: ![]() Сделаем
грубые оценки: log213 ≈ 4 и log221 ≈ 2.
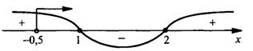
Поэтому данная дробь имеет положительный знак. Теперь, учитывая ОДЗ выражения,
строим диаграмму его знаков. Из диаграммы видно, что решения неравенства -
промежуток х ∈ [1; 2).
Сделаем
грубые оценки: log213 ≈ 4 и log221 ≈ 2.
Поэтому данная дробь имеет положительный знак. Теперь, учитывая ОДЗ выражения,
строим диаграмму его знаков. Из диаграммы видно, что решения неравенства -
промежуток х ∈ [1; 2).
Особенно полезен метод интервалов, если в неравенство входят выражения разных типов.
Пример 7
Решим
неравенство ![]()
Очевидно,
что ОДЗ неравенства х > 4. Числитель дроби обращается в нуль при х = 7,
знаменатель - 1 при х = -1 и х = 5. Отметим эти точки на координатной оси.
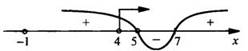
Определим знак данного выражения. Например, при х = 13 получаем: ![]() С
учетом ОДЗ выражения строим диаграмму его знаков. Из диаграммы получаем решения
неравенства х ∈ (4; 5) U [7; +∞).
С
учетом ОДЗ выражения строим диаграмму его знаков. Из диаграммы получаем решения
неравенства х ∈ (4; 5) U [7; +∞).
IV. Задание на уроке
§ 45, № 3 (а, б); 5 (в, г); 7 (б); 9 (а, б); 10 (б); 12 (а, б); 13 (в); 16 (б); 17 (a); 18 (б).
V. Задание на дом
§ 45, № 3 (в, г); 5 (а, б); 7 (г); 9 (в, г); 10 (г); 12 (в, г); 13 (г); 15 (б); 16 (a); 17 (б); 18(a).
VI. Творческие задания
Решите неравенство:

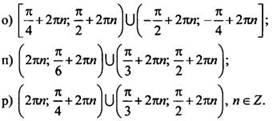
VII. Подведение итогов урока
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.