алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Переход к новому основанию логарифма - Показательная и логарифмическая функции

Цель: найти связь между логарифмами с разными основаниями от данного числа.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

Решите неравенство:

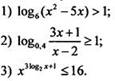
Вариант 2

Решите неравенство:

III. Изучение нового материала

В процессе изучения темы встречались логарифмы с самыми разными основаниями. Возникает естественный вопрос: существует ли связь между логарифмами с разными основаниями данного числа, т. е. как связаны между собой log_a b и log_c b? На этот вопрос отвечает следующая теорема.

Теорема. Если а, b, с - положительные числа и а, с ≠ 1, то выполняется равенство  (формула перехода к новому основанию логарифма).

Докажем это утверждение. Введем обозначения: х = log_a b, у = log_c b, z = log_c a. Надо доказать, что  Из введенных обозначений следует, что  Последнее равенство возведем в степень х и получим: (с^z)^х = а^х или zx = а^х. Сравнивая это равенство с равенствами а^х = b = с^y, имеем: c^zx = c^y, откуда zx = у и х = y/z, т. е. 

Пример 1

По полученной формуле перехода к новому основанию логарифма, например, имеем: 

Формула полезна тем, что позволяет переходить в логарифмах к любому новому основанию, необходимому по условию задачи.

Пример 2

Вычислим выражение 

Так как основания логарифмов разные, то перейдем к одному основанию, например 3. При этом  Тогда получаем: 

Пример 3

Решим уравнение 

В логарифмах перейдем к одному основанию, например числу 2. Получаем:  или  Чтобы избавиться от дробных множителей, умножим все члены уравнения на число 6. Имеем:  или 11log₂x = 33, откуда log₂x = 3 и x = 2³ = 8.

Пример 4

Решим уравнение 

Перейдем в логарифмах к основанию 5 и получим:  или  или  или  Так как log₅10 ≠ 0, то, разделив обе части уравнения на эту величину, получим log₅x = log₅2, откуда х = 2.

Разумеется, формула перехода к новому основанию используется и при решении более сложных задач.

Пример 5

Найдем:

Тогда имеем: 

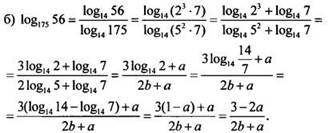
В данном примере необходимо было найти log₁₄2, поэтому число 2 пришлось выразить через числа 14 и 7 (2 = 14/7), логарифмы которых по основанию 14 были известны.

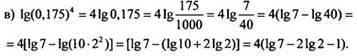
Таким образом, задача будет решена, если удастся найти lg7 и lg2 по известным значениям lg196 = с и lg56 = d. Имеем:  Если обозначить lg 2 = x, lg 7 = у, to для их определения получаем систему линейных уравнений:  Из нижнего уравнения имеем: у = d - 3х. Подставляя это выражение в верхнее уравнение, получим: 2x + 2(d - 3х) = с или -4х + 2d = с, откуда  Тогда  Учтем, что 

Пример 6

Решим уравнение 

Установить ОДЗ этого уравнения достаточно трудно, так как пришлось бы решать логарифмические неравенства, поэтому отметим пока что х > 1. Перейдем в первом логарифме к основанию 0,2:  - и введем замену  Тогда уравнение имеет вид:  Определим ОДЗ этого уравнения из условий 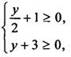 т. е. у ∈ [-2; +∞). Решим это уравнение, уединив один радикал  и возведя равенство в квадрат:  Тогда  Еще раз возведя в квадрат, получим: 16у + 48 = у² + 12у + 36 или у² - 4у - 12 = 0. Корни этого уравнения у₁ = -2, у₂ = 6 входят в ОДЗ исходного уравнения, однако проверка показывает, что у₂ = 6 исходному уравнению не удовлетворяет.

Итак, получаем простейшее логарифмическое уравнение:  откуда  и х = 26.

Отметим два следствия из приведенной теоремы, которые достаточно часто используются при решении задач (предлагается доказать самостоятельно).

Следствие 1. Если а и b положительные числа, отличные от 1, то справедливо равенство 

Следствие 2. Если а и b положительные числа и а ≠ 1, то для любого числа r ≠ 0 справедливо равенство 

IV. Задание на уроке

§ 46, № 1 (а, б); 2; 5 (в, г); 7 (а); 8 (б); 9 (а, г); 10 (а); 11; 13 (а); 14 (б); 15 (a); 16 (б).

V. Задание на дом

§ 46, № 1 (в, г); 3; 5 (а, б); 7 (б); 8 (а); 9 (б, в); 10 (б); 12; 13 (б); 14 (а); 15 (б); 16 (a).

VI. Творческие задания

1. Упростите выражение:

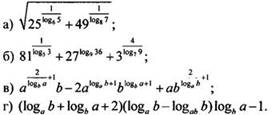
Ответы: 

2. Решите уравнение:

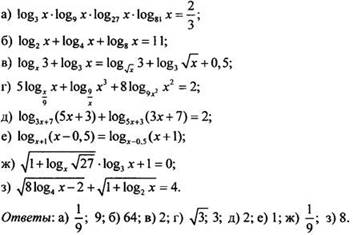
VII. Подведение итогов урока