алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Таблица первообразных. Три правила нахождения первообразных - Первообразная - Первообразная и интеграл

Цель: отработать практические навыки интегрирования.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Сформулируйте основное свойство первообразной.

2. Найдите общий вид первообразных для функции f(х) и напишите ту первообразную, график которой проходит через точку А:

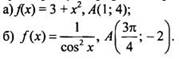
Вариант 2

1. Объясните геометрический смысл основного свойства первообразной.

2. Найдите общий вид первообразных для функции f(x) и напишите ту первообразную, график которой проходит через точку A:

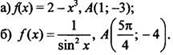
III. Изучение нового материала

Для дальнейшей работы необходимо знать первообразные для основных (изучаемых в школе) функций (см. таблицу) и правила интегрирования.

Таблица первообразных для функций

Приведенную таблицу легко проверить, выполнив обратную операцию - продифференцировать функцию F(x) и сравнить результат с функцией f(х) (рекомендуем сделать это самостоятельно).

Следующий шаг в изучении рассматриваемой темы - правила интегрирования и их применение для нахождения первообразных функций. Эти правила похожи на соответствующие правила дифференцирования.

Правило 1. Если функция F(x) - первообразная для функции f(x), a G(х) - первообразная для g(x), то функция F(x) + G(x) - первообразная для функции f(x) + g(x). Можно сформулировать короче: первообразная для суммы функций равна сумме первообразных каждой функции.

Используя определение первообразной, имеем: F'(x) = f(x) и G’(x) = g(x), тогда 

Пример 1

Найдем первообразную для функции 

Учтем, что функция  представляет собой алгебраическую сумму трех функций. Используя таблицу первообразных и правило 1, найдем: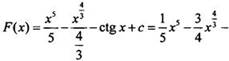 

Правило 2. Если функция F(x) - первообразная для функции f(х), а k - постоянная, то функция kF(х) - первообразная для функции kf(x). Или короче: первообразная для произведения числа и функции равна произведению числа на первообразную функции.

Исходя из определения первообразной и используя правило дифференцирования, получаем: 

Пример 2

Найдем первообразную функции 

Используя рассмотренное правило и таблицу первообразных, получаем: 

Правило 3. Если функция F(x) - первообразная для функции f(х), то функция  - первообразная для функции f(kх + m), где k и m — постоянные. Короче: первообразная для функции, зависящей от аргумента kх + m (где k и m - постоянные), равна произведению числа 1/k на первообразную для функции от х при значении аргумента kх + m.

Учитывая правило дифференцирования сложной функции, получаем: 

Пример 3

Найдем первообразную функции 

Так как первообразная для функции cos х есть функция sin х, то в соответствии с правилом 3 первообразная для функции  - функция 

Пример 4

Найдем первообразную для функции 

Запишем функцию в виде  Так как первообразная для функции х^-7 есть функция  то первообразная для f(x) — функция 

Разумеется, три рассмотренных правила интегрирования можно использовать совместно.

Пример 5

Найдем первообразную для функции 

Учитывая правила 1 - 3, найдем первообразную для данной функции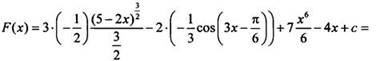 

Как и ранее, разобранные правила используются и при решении физических задач.

Пример 6

Точка массой m = 2 кг движется вдоль оси Ох под действием силы, направленной вдоль этой оси и равной  Найдите закон x(t) движения точки, если при t = 2/3 с скорость точки равна 23/9 м/с, координата равна 40/81 м. Здесь F - сила в ньютонах, t - время в секундах, х - путь в метрах.

По второму закону Ньютона F = mа (где а - ускорение тела), откуда  Для данной задачи имеем: 

Скорость тела v(t) есть первообразная для ее ускорения a(t). Поэтому находим  Постоянную c₁ определим, используя начальное условие  Получаем равенство  откуда c₁ = 2. Тогда скорость тела меняется по закону 

Аналогично координата x(t) есть первообразная для скорости v(t). Поэтому получаем 

 Для нахождения постоянной с₂ вновь используем начальное условие  Имеем равенство:  или  откуда  Итак, закон движения точки 

В заключение урока сделаем ряд важных замечаний.

1. Имеется существенное отличие в правилах интегрирования и дифференцирования. Не существует правил для нахождения первообразных от произведения функций, частного функций, сложной функции (при нахождении производных такие правила имеют место).

2. В связи с п. 1 процесс интегрирования намного сложнее операции дифференцирования. Например, нахождение первообразных для функций   и т. д. является достаточно сложной задачей и требует применения разнообразных приемов. В то же время вычисление производных от этих функций никакого труда не составляет.

3. В соответствии с п. 1 первообразные для некоторых функций (например,  и т. д.) существуют, но не могут быть записаны с помощью элементарных функций.

4. Первообразная функция в курсе математического анализа называется неопределенным интегралом (в этом курсе понятия первообразной не существует). Причины такого термина будут понятны на следующих уроках.

IV. Контрольные вопросы (фронтальный опрос)

1. Первообразные основных элементарных функций.

2. Три правила нахождения первообразных.

V. Задание на уроках

§ 48, № 3 (а); 5 (б, в); 6 (а, б); 7 (б, в); 8 (а, г); 9 (а, б); 10 (в, г); 11 (а, г); 15; 17 (а, б); 18 (а); 19; 20 (а); 21 (б, в); 22 (а).

VI. Задание на дом

§ 48, № 3 (б); 5 (а, г); 6 (в, г); 7 (а, г); 8 (б, в); 9 (в, г); 10 (а, б); 11 (б, в); 16; 17 (в, г); 18 (б); 20 (б); 21 (а); 22 (б).

VII. Подведение итогов уроков