алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Интегрирование функций с помощью их преобразования (факультативное занятие) - Первообразная - Первообразная и интеграл

Цель: рассмотреть некоторые приемы интегрирования функций.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Найдите первообразную функции:

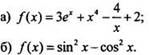
2. Найдите ту первообразную функцию f(x) = 4х + 7, график которой касается оси абсцисс.

Вариант 2

1. Найдите первообразную функции:

2. Найдите ту первообразную функцию f(x) = 6х - 4, график которой касается оси абсцисс.

III. Изучение нового материала

Разумеется, первообразную можно найти только для тех функций, которые приведены в таблице. Поэтому основной принцип интегрирования - приведение более сложных функций к тем, которые даны в таблице. Существуют следующие методы интегрирования:

1. Метод непосредственного (табличного) интегрирования (был рассмотрен на предшествующих уроках).

2. Метод замены переменной интегрирования. Простейший случай линейной замены (нахождение первообразной функции f(kx + m)) был также рассмотрен на предыдущих занятиях.

3. Метод преобразования функции в сумме функций будет рассмотрен на этом уроке.

4. Метод интегрирования по частям достаточно сложен и будет изучаться в вузе.

Ранее отмечалось, что одна из сложностей при интегрировании состоит в отсутствии формул для первообразных произведения и частного функций. Поэтому необходимо произведение и частное функций представить в виде суммы функций (если это возможно). На примерах рассмотрим самые типичные ситуации.

Пример 1

Найдем первообразную функции f(x) = (3х + 1)(2х - 3).

Умножим многочлены и запишем функцию в виде f(x) = 6х² - 7х - 3. Первообразную такой функции уже легко найти: 

Пример 2

Найдем первообразную функции 

В данной функции выделим целую часть. Для этого столбиком разделим числитель на знаменатель и получим Найдем первообразную такой функции: 

Пример 3

Найдем первообразную функции 

Прежде всего заметим, что квадратный трехчлен х² + 2х - 15 имеет корни и может быть разложен на множители: х² + 2х - 15 = (х – 3)(x + 5). Очевидно, что дробь  может получиться при сложении дробей со знаменателями х - 3 и х + 5. При этом числители дробей неизвестны. Обозначим их величинами а и b соответственно (где a и b - некоторые числа) и представим дробь в виде  В правой части равенства приведем дроби к общему знаменателю:  Получили равенство  которое выполняется, если  Решение этой системы линейных уравнений а = 2 и b = 3. Таким образом, имеем:  Теперь легко найти первообразную функции: 

Пример 4

Найдем первообразную функции 

Избавимся от иррациональности в знаменателе функции. Для этого числитель и знаменатель дроби умножим на величину, сопряженную знаменателю. Ползаем:  Найдем первообразную этой функции: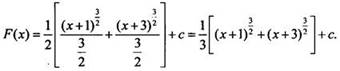 

Очень часто при интегрировании дробей используют почленное деление числителя на знаменатель.

Пример 5

Найдем первообразную функции 

Почленно разделим числитель на знаменатель и запишем функцию в виде  Теперь легко найти первообразную функции: 

Пример 6

Найдем первообразную функции f(x) = tg²x.

Используем основное тригонометрическое тождество и запишем функцию в виде  Найдем первообразную этой функции: F(x) = tg х - х + с.

При интегрировании тригонометрических функций часто используют различные тригонометрические формулы.

Пример 7

Найдем первообразную функции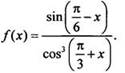 

Используем формулу приведения и преобразуем функцию: 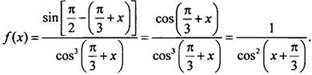 Найдем первообразную функции 

Пример 8

Найдем первообразную функции 

Используя метод вспомогательного угла, преобразуем выражение  и получим:  Тогда функция имеет вид  Используем формулу понижения степени 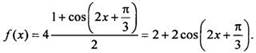 Найдем первообразную такой функции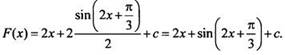 

Пример 9

Найдем первообразную функции f(x) = sin⁴x.

Вновь дважды используем формулу понижения степени и запишем функцию в виде 

 Находим первообразную такой функции: 

И наконец, очень часто используют формулы преобразования произведения тригонометрических функций в сумму функций.

Пример 10

Найдем первообразную функции 

Преобразуем произведение косинусов в их сумму и запишем функцию в виде  Найдем первообразную этой функции: 

IV. Задания на уроках и дома

Найдите первообразную функции:

Ответы из-за их громоздкости не приводятся.

V. Подведение итогов уроков