
Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год
Задачи, приводящие к понятию определенного интеграла. Понятие определенного интеграла - Определенный интеграл - Первообразная и интеграл
Цель: рассмотреть типичные задачи, связанные с определенным интегралом, и его понятие.
Ход уроков
I. Сообщение темы и цели уроков
II. Изучение нового материала
Типичные задачи
Задача 1. Площадь криволинейной трапеции.
В курсе геометрии были получены формулы для вычисления площадей простейших фигур (треугольники и некоторые многоугольники) и объемов тел (призмы, пирамиды, цилиндры, конусы, шары). В то же время круг таких задач намного разнообразнее, и необходимо рассмотреть общий подход к подобным задачам.
Сначала рассмотрим понятие криволинейной трапеции. Пусть на отрезке [а; b] оси абсцисс задана непрерывная функция f(x), не меняющая на нем знака. Фигуру, ограниченную графиком этой функции, отрезком [a; b] и прямыми х = а и х = b, называют криволинейной трапецией.
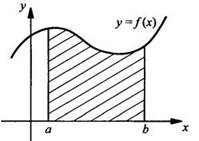
Было бы заманчиво научиться вычислять площади криволинейных трапеций в случае произвольных функций f(х).
Разобьем отрезок [а; b] на n равных частей точками х1, х2, ..., хn. Построим прямоугольники со сторонами xk+1 – хk и f(хk).
![]()
Площадь такого прямоугольника равна
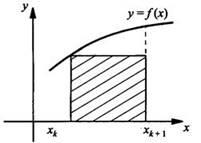
![]() (где
Δхk - длина отрезка [хk; хk+1], т.
е. Δхk = хk+1 - хk). Если такую
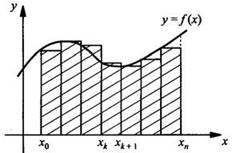
процедуру проделать для всех значений х (х = 0, 1, 2, ..., n - 1), то площадь
криволинейной трапеции S можно приближенно оценить площадью ступенчатой фигуры.
(где
Δхk - длина отрезка [хk; хk+1], т.
е. Δхk = хk+1 - хk). Если такую
процедуру проделать для всех значений х (х = 0, 1, 2, ..., n - 1), то площадь
криволинейной трапеции S можно приближенно оценить площадью ступенчатой фигуры.
![]() При
этом
При
этом ![]()
![]() (хотя
такое условие необязательно).
(хотя
такое условие необязательно).
Итак,
S ≈ Sn, и это приближенное равенство тем точнее, чем больше и,
т. к. на маленьком по длине отрезке [хk; хk+1] функция
f(х) меняется очень незначительно. Будем считать, что площадь криволинейной
трапеции S равна пределу последовательности (Sn), т. е. ![]()
Задача 2. Масса неоднородного стержня.
Дан прямолинейный неоднородный стержень, концы которого имеют координаты х = а и х = b. Плотность стержня в точке х может быть вычислена по формуле ρ = ρ(х). Найдем массу стержня.
![]()
Из курса физики известно, что масса Δm стержня длиной Δх с линейной плотностью р вычисляется по формуле Δm = ρΔх. Для решения данной задачи используем алгоритм задачи 1.
1) Разобьем отрезок [а; b] на n равных частей.
2) Рассмотрим частичный отрезок [хk; хk+1] и будем считать, что плотность во всех точках этого отрезка постоянна и равна ρ(хk).
3)
Найдем приближенное значение массы этого отрезка ![]()
4)
Найдем приближенное значение массы т всего стержня m ≈ Sn,
где ![]()
5)
Точное значение массы стержня равно пределу последовательности (Sn),
т. е. ![]()
Задача 3. Перемещение точки.
По прямой движется точка, скорость которой в зависимости от времени вычисляется по формуле v = v(t). Найдем перемещение точки за промежуток времени [а; b].
Напомним, что при равномерном движении с постоянной скоростью v перемещение S вычисляется по формуле S = vt. Для решения нашей задачи используем уже рассмотренные идеи.
1) Разделим промежуток времени [а; b] на n равных частей.
2) Рассмотрим промежуток времени [tk; tk+1] и будем считать, что за этот промежуток времени скорость тела была постоянной и равнялась v(tk).
3)
Найдем приближенное значение перемещения Sk точки за промежуток
времени [tk; tk+1]. Это значение равно ![]()
4)
Найдем приближенное значение перемещения S ≈ Sn, где ![]()
5)
Перемещение равно пределу последовательности (Sn), т. е. ![]()
Решение трех рассмотренных и (многих) других задач приводит к одной и той же математической модели. Такая модель должна быть изучена и приспособлена к решению реальных задач. Пока эта модель достаточно сложна, что видно из следующего примера.
Пример 1
Найдем площадь криволинейной трапеции, ограниченной осью абсцисс, параболой у = х2 и прямой х = 1.
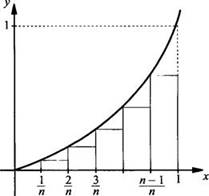
Построим
график функции у = х2. Разобьем отрезок интегрирования [0; 1] на n
равных частей. Будем аппроксимировать криволинейную трапецию объединением
прямоугольников, построенных под такой трапецией. На каждом промежутке ![]() строим
прямоугольник высотой
строим
прямоугольник высотой ![]() где
k = 1, 2, 3, ..., n - 1, n. Площадь такого прямоугольника равна
где
k = 1, 2, 3, ..., n - 1, n. Площадь такого прямоугольника равна ![]() Сумма
площадей всех подобных прямоугольников составляет
Сумма
площадей всех подобных прямоугольников составляет ![]() Теперь
нужно найти сумму квадратов натуральных чисел 1, 2, ..., n - 2, n - 1. Для
этого воспользуемся хорошо известной в математике формулой
Теперь
нужно найти сумму квадратов натуральных чисел 1, 2, ..., n - 2, n - 1. Для
этого воспользуемся хорошо известной в математике формулой ![]() Тогда
получаем:
Тогда
получаем: ![]()
![]() Очевидно,
что при n → ∞ величина 1/n → 0, и тогда
Очевидно,
что при n → ∞ величина 1/n → 0, и тогда ![]() Итак,
получили:
Итак,
получили: ![]() т.
е. площадь данной криволинейной трапеции равна 1/3.
т.
е. площадь данной криволинейной трапеции равна 1/3.
Понятие определенного интеграла
При рассмотрении трех типичных задач для непрерывной на отрезке [a; b] функции f(х) была использована следующая математическая модель.
1) Отрезок [а; b] разбивался на п равных частей.
2)
Составлялась сумма ![]() (эту
сумму называют интегральной суммой).
(эту
сумму называют интегральной суммой).
3)
Вычислялся ![]() Доказывается,
что такой предел существует. Его называют определенным интегралом от
функции f(х) на отрезке [а; b] и обозначают символом
Доказывается,
что такой предел существует. Его называют определенным интегралом от
функции f(х) на отрезке [а; b] и обозначают символом ![]() (читается:
интеграл от а до b эф от икс дэ икса). Числа а и b называются пределами
интегрирования: а — нижним пределом, b - верхним. Знак ∫
называют знаком интегрирования. Функция f(х) называется подынтегральной
функцией, переменная х - переменной интегрирования.
(читается:
интеграл от а до b эф от икс дэ икса). Числа а и b называются пределами
интегрирования: а — нижним пределом, b - верхним. Знак ∫
называют знаком интегрирования. Функция f(х) называется подынтегральной
функцией, переменная х - переменной интегрирования.
Вернемся
к трем рассмотренным задачам. Тогда площадь S криволинейной трапеции (задача 1)
можно записать в виде ![]() В
этом состоит геометрический смысл определенного интеграла.
В
этом состоит геометрический смысл определенного интеграла.
Массу
m прямолинейного стержня с плотностью ρ(х) (задача 2) можно записать в
виде ![]() В
этом состоит физический смысл определенного интеграла.
В
этом состоит физический смысл определенного интеграла.
Перемещение
S точки, движущейся по прямой со скоростью v(t) (задача 3) можно записать в
виде ![]() В
этом также заключается физический смысл определенного
интеграла.
В
этом также заключается физический смысл определенного
интеграла.
Учитывая широту применения интегрирования, понятию определенного интеграла можно придавать самый различный геометрический, физический, технический и т.д. смысл.
Формула Ньютона-Лейбница
Пока введенное понятие определенного интеграла мало что дает — появился новый символ. Необходимо научиться вычислять такие интегралы. Оказывается, определенный интеграл связан с первообразной.
Теорема. Если функция f(х) непрерывна на отрезке [а; b], то справедлива
формула ![]() где
F(x) - первообразная для f(х). Такую формулу называют формулой
Ньютона-Лейбница.
где
F(x) - первообразная для f(х). Такую формулу называют формулой
Ньютона-Лейбница.
На
практике вместо записи F(b) - F(a) используют запись ![]() (ее
иногда называют двойной подстановкой). Тогда формулу Ньютона-Лейбница можно
записать в виде
(ее
иногда называют двойной подстановкой). Тогда формулу Ньютона-Лейбница можно
записать в виде ![]()
При вычислении определенного интеграла находят первообразную F(x) для функции f(х), вычисляют ее значение для верхнего F(b) и нижнего F(a) пределов интегрирования и находят их разность F(b) - F(a).
Пример 2
Вычислим ![]()
Первообразная
для функции f(x) = х2 есть функция ![]() Тогда
Тогда ![]() Сравните
эти вычисления с вычислениями примера 1.
Сравните
эти вычисления с вычислениями примера 1.
Пример 3
Вычислим ![]()
Первообразная
для функции ![]() (формула
понижения степени) есть функция
(формула
понижения степени) есть функция ![]() Тогда
Тогда 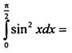
![]()
Пример 4
Вычислим ![]()
Первообразная
для функции ![]() есть
функция F(x) = ln|х|. Тогда
есть
функция F(x) = ln|х|. Тогда ![]()
Давайте
теперь уточним терминологию. Будем придерживаться терминов, принятых в курсе
математического анализа, изучаемого в вузах. Исходя из структуры формулы
Ньютона-Лейбница ![]() первообразную
функцию F(x) называют неопределенным интегралом и обозначают
символом
первообразную
функцию F(x) называют неопределенным интегралом и обозначают
символом ![]() т.
е.
т.
е. ![]() Такой
термин связан с тем, что для функции f(x) существует бесконечно много
первообразных, т. е. первообразная однозначно не определена. Соответственно,
число
Такой
термин связан с тем, что для функции f(x) существует бесконечно много
первообразных, т. е. первообразная однозначно не определена. Соответственно,
число ![]() по
аналогии называют определенным интегралом, т. к. это вполне
конкретное число. Заметим, что по определению первообразной (неопределенного
интеграла) справедливо равенство
по
аналогии называют определенным интегралом, т. к. это вполне
конкретное число. Заметим, что по определению первообразной (неопределенного
интеграла) справедливо равенство ![]()
Пример 5
Вычислим 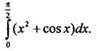
Сначала
найдем неопределенный интеграл ![]() затем
определенный интеграл
затем
определенный интеграл ![]()
![]()
Очень часто при вычислении определенных интегралов полезно использовать их геометрический смысл - площадь соответствующей криволинейной трапеции.
Пример 6
Используя геометрический смысл интеграла, вычислим:
![]()
Построим график подынтегральной функции f(х) = |х - 1|.
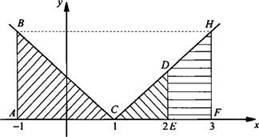
а)
Видно, что значение данного интеграла равно площади многоугольника ABCDE,
состоящего из двух прямоугольных равнобедренных треугольников: АВС (АВ = АС =
2) и СОЕ (СЕ = ED = 1). Тогда ![]()
б)
Значение данного интеграла равно площади трапеции EDHF с основаниями ED = 1 и
HF = 2 и высотой EF = 1. Поэтому ![]()
![]()
Пример 7
Используя
геометрический смысл интеграла, вычислим ![]()
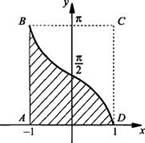
Построим
график подынтегральной функции f(x) = arccos x. Также построим прямоугольник
ABCD и измерениями АD = 2 и АВ = π и площадью S = AD ∙ AB = 2π.
Видно, что площадь криволинейной трапеции АВD составляет ровно половину площади
прямоугольника ABCD. Поэтому ![]()
Пример 8
Используя геометрический смысл интеграла, вычислим:
![]()
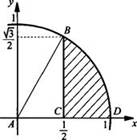
Построим
график подынтегральной функции ![]() Очевидно,
что у ≥ 0. Возведем обе части равенства в квадрат: у2 = 1
- х2 или х2 + у2 = 1. Получили
уравнение окружности с центром в начале координат и радиуса 1. Поэтому с учетом
условия у ≥ 0 графиком данной функции является верхняя полуокружность.
Очевидно,
что у ≥ 0. Возведем обе части равенства в квадрат: у2 = 1
- х2 или х2 + у2 = 1. Получили
уравнение окружности с центром в начале координат и радиуса 1. Поэтому с учетом
условия у ≥ 0 графиком данной функции является верхняя полуокружность.
а)
Значение данного интеграла равно площади четверти круга радиуса 1.Поэтому ![]()
б)
Значение этого интеграла равно площади криволинейной трапеции BCD. Эта площадь
равна разности площади сектора ABD (с углом π/3): ![]() -
и площади прямоугольного треугольника АВС:
-
и площади прямоугольного треугольника АВС: ![]() Поэтому
значение данного интеграла
Поэтому
значение данного интеграла ![]()
Заметим,
что в примерах 7 и 8 были найдены соответствующие определенные интегралы,
исходя из геометрического смысла. В то же время нахождение аналогичных неопределенных
интегралов представляет достаточно серьезную задачу. Кроме того, эти интегралы
и выглядят сложно, например: ![]() и
и ![]()
Таким образом, геометрический смысл определенного интеграла во многих задачах очень полезен при его вычислении.
III. Контрольные вопросы
1. Понятие криволинейной трапеции.
2. Задачи, приводящие к понятию определенного интеграла.
3. Понятие определенного интеграла.
4. Геометрический и физический смысл определенного интеграла.
5. Формула Ньютона - Лейбница.
IV. Задание на уроках
§ 49, № 1 (а, б); 2 (в, г); 4 (а, б); 5 (в, г); 6 (а, г); 7 (в, г); 8 (а, б); 9 (в, г); 10 (a).
V. Задание на дом
§ 49, № 1 (в, г); 2 (а, б); 4 (в, г); 5 (а, б); 6 (б, в); 7 (а, б); 8 (в, г); 9 (а, б); 10 (б).
VI. Подведение итогов уроков
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.