алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Итоги контрольной работы - Урок 3 - Определенный интеграл - Первообразная и интеграл

Цели: сообщить результаты работы; рассмотреть наиболее типичные ошибки; разобрать трудные задачи.

Ход урока

I. Сообщение темы и целей урока

II. Итоги контрольной работы

III. Ответы и решения

Ответы

Вариант 1

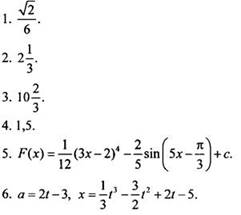
Вариант 2

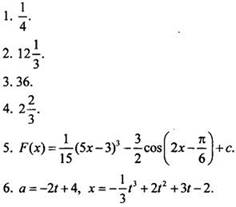
Вариант 3

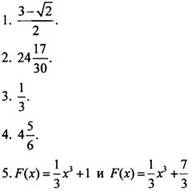 (учесть, что в точке касания F(x) = f₂(х) и f₁(х) = f₂(х)).

Вариант 4

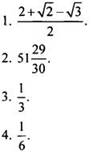
 (учесть, что в точке касания F(x) = f₂(х) и f₁(х) = f₂(х)).

Решения

Вариант 5

1. Используем правило интегрирования функций f(kx + m) и получим:  

Ответ: 

2. Разложим подынтегральную функцию в сумму функций:

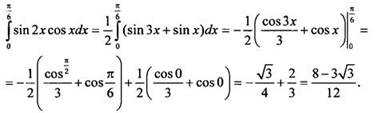
Ответ: 

3. Раскроем знак модуля, построим график подынтегральной функции и вычислим площадь полученной фигуры.

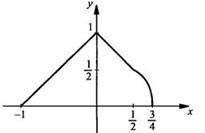
Имеем: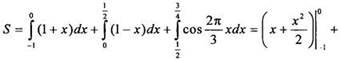 

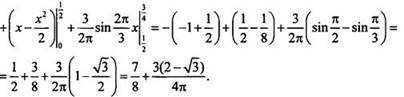
Ответ: 

4. Используем формулу понижения степени и преобразуем подынтегральную функцию:  Площадь искомой фигуры 

Ответ: 

5. В функции  разложим знаменатель на множители и запишем ее в виде:  Теперь найдем общий вид первообразных: 

Ответ: 

6. Пусть дана функция F(x). Тогда тангенс угла наклона касательной по условию задачи tga = F'(x) = 3х² в каждой точке х. Таким образом, надо найти первообразную F(x) для функции f(x) = 3х². Получаем: F(x) = х³ + с. Так как график этой первообразной проходит через точку A(1; 2), то координаты этой точки удовлетворяют уравнению первообразной. Имеем равенство 2 = 1³ + с, откуда постоянная с = 1. Таким образом, уравнение заданной кривой F(x) = х³ + 1.

Ответ: F(x) = х³ + 1.

Вариант 6

1. Используем правило интегрирования функций f(kx + m) и получим:  

Ответ: 

2. Разложим подынтегральную функцию в сумму функций:

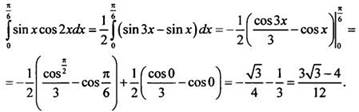
Ответ: 

3. Раскроем знак модуля, построим график подынтегральной функции и вычислим площадь полученной фигуры.

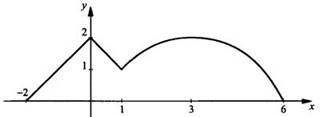
Имеем: 

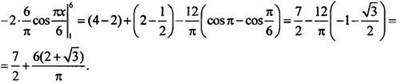
Ответ: 

4. Используем формулу понижения степени и преобразуем подынтегральную функцию:  Площадь искомой фигуры 

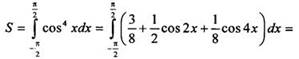
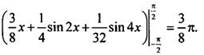
Ответ: 

5. В функции  разложим знаменатель на множители и запишем ее в виде:  Теперь найдем общий вид первообразных: 

Ответ: 

6. Пусть дана функция F(x). Тогда тангенс угла наклона касательной по условию задачи tga = F'(x) = 2х в каждой точке х. Таким образом, надо найти первообразную F(x) для функции f(x) = 2х. Получаем: F(x) = х² + с. Так как график этой первообразной проходит через точку А(2; 5), то координаты этой точки удовлетворяют уравнению первообразной. Имеем равенство 5 = 2² + с, откуда постоянная с = 1. Таким образом, уравнение заданной кривой F(x) = х² + 1.

Ответ: F(x) = х² + 1.