алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Зачетная работа по теме Первообразная и интеграл - Определенный интеграл - Первообразная и интеграл

Цель: проверить знания учащихся по вариантам одинаковой сложности.

Ход уроков

I. Сообщение темы и цели уроков

II. Варианты зачетной работы

Вариант 1

А

1. Докажите, что функция F(x) = 3 + 4 sin2x является первообразной для функции f(x) = 8 cos 2x при x ∈ R.

2. Для функции  найдите первообразную, график которой проходит через точку А(2; 4). Постройте график этой функции.

3. Найдите общий вид первообразных для функции:

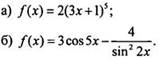
4. Вычислите площадь фигуры, ограниченной линиями у = х³ + 2х, у = 0, х = 1, х = 2.

5. Найдите площадь лунки, ограниченной синусоидами у = 3sin x и у = sin х, 0 ≤ х ≤ π.

6. Точка движется по прямой со скоростью v(t) = 4t + sin πt. Найдите путь, пройденный точкой за время от t₁ = 1 до t₂ = 5.

В

7. Вычислите площадь фигуры, ограниченной линиями 

8. Найдите неопределенные интегралы (первообразные):

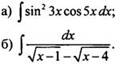
9. Вычислите площадь фигуры, ограниченной графиком функции f(х) = х³ - 3х и касательной к этому графику, проведенной в точке a = -1.

C

10. Найдите 

11. Из геометрических соображений вычислите интеграл 

12. Из точки (0; с) проведены касательные к параболе f(x) = 1 - х². При каком значении с площадь фигуры, ограниченной этими касательными и параболой, равна 18?

Вариант 2

А

1. Докажите, что функция F(x) = 7 + 5 cos 3х является первообразной для функции f(х) = -15 sin 3х при х ∈ R.

2. Для функции  найдите первообразную, график которой проходит через точку А(1; 2). Постройте график этой функции.

3. Найдите общий вид первообразных для функции:

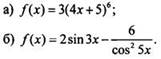
4. Вычислите площадь фигуры, ограниченной линиями у = х³ + 4х, у = 0, х = 1, х = 3.

5. Найдите площадь лунки, ограниченной косинусоидами у = 4 cos x и 

6. Точка движется по прямой со скоростью v(t) = 6t + 2 sin πt. Найдите путь, пройденный точкой за время от t₁ = 3 до t₂ = 5.

В

7. Вычислите площадь фигуры, ограниченной линиями  

8. Найдите неопределенные интегралы (первообразные):

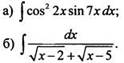
9. Вычислите площадь фигуры, ограниченной графиком функции  и касательной к этому графику, проведенной в точке a = -1.

С

10. Найдите 

11. Из геометрических соображений вычислите интеграл 

12. Из точки (0; с) проведены касательные к параболе f(x) = 3 - х². При каком значении с площадь фигуры, ограниченной этими касательными и параболой, равна 144?

III. Ответы и решения

Вариант 1

Ответы

1. Доказано.

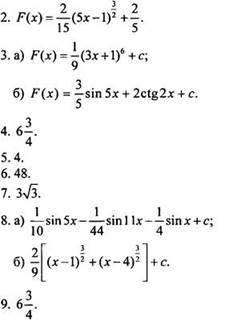
10. Знаменатель подынтегральной функции  разложим на множители и запишем ее в виде:  Попытаемся представить функцию f(х) в виде суммы двух дробей со знаменателями х - 1 и х + 2 и числителями а и b. т. е.  Сложим эти дроби:  Имеем равенство:  которое выполняется при условиях  Решение этой системы уравнений а = 2 и b = 3. Тогда функция f(x) имеет вид:  Получаем: 

Ответ: 

11. Построим график подынтегральной функции  Получаем:  (где y - 5 ≥ 0, т. е. y ≥ 5) или х² +(у - 5)² = 2². Это уравнение верхней полуокружности с центром в точке A(0; 5) и радиуса 2. Теперь легко вычислить площадь построенной фигуры, состоящей из прямоугольника (с размерами 4 и 5) и полукруга радиуса 2. Получаем: 

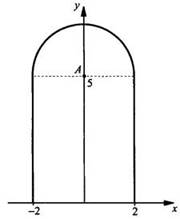
Ответ: 20 + 2π.

12. Очевидно, что парабола f(x) = 1 – х² и касательные к ней симметричны относительно оси ординат. Поэтому достаточно вычислить площадь криволинейной трапеции АВС, которая по условию будет равна 9. Предположим, что касание происходит в точке а. Получим уравнение касательной АС.

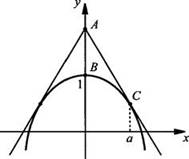
Найдем f(x) = -2х. Тогда уравнение касательной имеет вид:  Так как касательная проходит через точку A(0; с), то с = а² + 1. Необходимо найти точку касания а. Для этого запишем площадь фигуры ABC:  Получаем уравнение  откуда а = 3. После этого находим 

Ответ: 10.

Вариант 2

Ответы

1. Доказано.

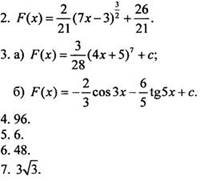
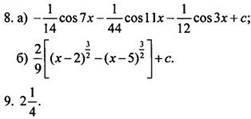
Решения

10. Знаменатель подынтегральной функции  разложим на множители и запишем ее в виде  Попытаемся представить функцию f(x) в виде суммы двух дробей со знаменателями х – 3 и х + 2 и числителями а и b, т. е.  Сложим эти дроби:  Имеем равенство:  которое выполняется при условиях  Решение этой системы уравнений а = 3 и b = 2. Тогда функция f(x) имеет вид:  Получаем: 

Ответ: 

11. Построим график подынтегральной функции 

Получаем:  (где 6 - у ≥ 0, т. е. у ≤ 6) или х² + (y - 6)² = 3². Это уравнение нижней полуокружности с центром в точке A(0; 6) и радиуса 3. Теперь легко вычислить площадь построенной фигуры, состоящей из квадрата (со стороной 6) без полукруга радиуса 3. Получаем: 

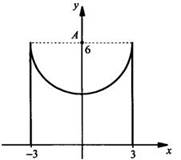
Ответ: 36 - 4,5π.

12. Очевидно, что парабола f(х) = 3 - х² и касательные к ней симметричны относительно оси ординат. Поэтому достаточно вычислить площадь криволинейной трапеции АВС, которая по условию будет равна 72. Предположим, что касание происходит в точке а. Получим уравнение касательной АС.

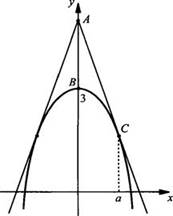
Найдем f’(x) = -2х. Тогда уравнение касательной имеет вид:  Так как касательная проходит через точку А(0; с), то с = а² + 3. Необходимо найти точку касания а. Для этого запишем площадь фигуры АВС:  Получаем уравнение  откуда а = 6. После этого находим с = а² + 3 = 6² + 3 = 39.

Ответ: 39.