Основная литература
	Яблонский СВ. Введение в дискретную математику. М.: Высшая школа, 2002	учебник			2
	Ершов Ю.Л., Палютин Е.А. Математическая логика. М.: Наука, 2007	учебник			4	2
Дополнительная лите а				а
	1. Мальцев А.И. Алгоритмы и рекурсивные функции. М. : Наука, 1986	учебник			2
	2.Лавров и.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. М.: Наука, 1975	учебник			З

В перечень основной литературы включаются основные учебники и пособия (как правило, три - четыре наименования) по дисциплинам социальногуманитарного профиля за последние 5 лет, по другим направлениям за последние 10 лет.

Дополнительная литература должна включать не более 10 наименований.

Тезисы лекционных занятий.

Тема 1. Основные понятия теории множеств. Способы задания множеств.

Операции над множествами и их свойства.

Понятие множества является одним из основных понятий математики и поэтому не определяется через другие. Его можно пояснить только на примерах. Так можно говорить о множестве студентов некоторого факультета, о множестве натуральных чисел и т. д. Математический смысл слова «множество» отличается от того, как оно используется в обыденной речи, где его связывают с большим числом предметов. В математике этого не требуется. Здесь рассматривают множество, состоящее из одного объекта, и множество, не содержащее ни одного объекта.

В некоторых случаях множества обозначают буквами латинского алфавита А В С . . .. Множество не содержащее ни одного объекта называют пустым и обозначают знаком б. Объекты, из которых состоит множество, называют его элементами. В математике и других науках нередко приходится выяснять, принадлежит какой-либо объект рассматриваемому множеству или не принадлежит. Предложение вида «Объект а принадлежит множеству А» можно записать используя символы: аеА. Прочитать его можно по разному верхнее, «а элемент множества А» «множество А содержит элемент а». Предложение «Объект а не принадлежит множеству А» можно записать так: а кА. Множества бывают конечные и бесконечные, так множество дней недели конечно, а множество точек на прямой или множество натуральных чисел - бесконечно.

Способы задания множеств. Как уже говорилось понятие множества мы используем без определения. Но как узнавать, является та или иная совокупность множеством или не является?

Считают, что множество определяется своими элементами, т. е. Множество задано , если о любом объекте можно сказать принадлежит он этому множеству либо не принадлежит.

Множество можно задать, перечислив все его элементы. При этом возможна запись А={З 4,5,6} , в которой перечисляемые элементы заключаются в фигурные скобки. Однако, если множество бесконечно, то его элементы перечислить нельзя. Трудно задать и конечное множество с большим числом элементов. В таких случаях применяют другой способ задания множеств: указывают характеристическое свойство его элементов.

Характеристическое свойство — это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит. Например, множество А двузначных чисел, символически А={х хдвузначное число } . Здесь характеристическое свойство «быть двузначным числом». Оно решает вопрос о том, принадлежит какой-либо объект множеству А или не принадлежит. Так 21 Е-А 125 КА. Случается, что одно и то же множество можно задать, указав различные характеристические свойства его элементов. Например, множество квадратов можно задать как множество прямоугольников с равными сторонами и как множество ромбов с прямыми углами. Другой пример, задание

числового множества М, порождающей процедурой: 1) 5 ем; 2) если аеМ, то — е а

М; З) если аеМ,  Нетрудно показать, что М={5            -4

54                          ' 5 ' 4

Иногда определить, обладает ли тот или иной объект заданным свойством, и тем более найти все такие объекты, может быть сложной задачей. Например, найти множество корней уравнения означает решить уравнение. Решение вопроса о том, существует ли процедура распознавания тех или иных свойств математических объектов, относится к теории алгоритмов.

Отношения между множествами.

Определение. Множество В называется подмножеством множества А, если каждый элемент множества В является элементом множества А. Символически это записывают ВсА. Считают, что ZcA и что АсА для любого множества А. Выпишем , например, все подмножества множества А={2,З,4} : б, А, {2},{3},{4}, {2,3}, {2,4}, {3,4} т.е. восемь подмножеств.

Определение. Множества А и В называются равными, если АсВ и ВсА.

Символически пишут А=В. из определения следует, что порядок записи элементов множества не существенен, т. е. Например, {2,3,4}={3,4,2}. Наглядно отношения между множествами изображают при помощи кругов (диаграмм) Эйлера. Для этого множества, сколько бы они не содержали элементов, представляют при помощи кругов, овалов, или любых других геометрических фигур.

в

Рис. 1

В ряде случаев целесообразно рассматривать универсальное множество У, т.е. все рассматриваемые в последующем множества являются подмножествами этого универсального множества У.

Операции над множествами и их свойства.

Если А и В множества, то с помощью теоретико-множественных операций могут быть получены другие множества.

Определение. Пересечением множеств А и В называется множество (символически АаВ), содержащее только такие элементы, которые принадлежат множеству А и множеству В, т.е. хеАпВ сэ хеА и х ЕВ. (Наглядно изобразить пересечение множеств

А и В можно с помощью диаграмм Эйлера)

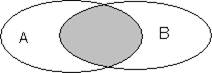
рис.2

Например: если А ={               В={2,З,5}, то АпВ={2,З}.

Определение 2. Объединением множеств А и В (символически АЛ) называется множество, содержащее только такие элементы, которые принадлежат множеству А или множеству В, т.е. хеАиВ сэ хеА или хеВ. Наглядное изображение рис.З

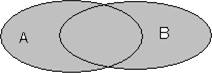
рис.З

Например: если А={            В={2,З,5}, то              1,2,3,5}.

Определение З. Разностью множеств А и В называется множество (символически А \ В), содержащее только такие элементы множества А, не принадлежащие множеству В

т.е. хеА \ В сэ хеА и хеВ. Наглядное изображение рис.4

рис.4

Например: А={            В={2,З,5}, то А \ В={ Ц.

Определение 4. Дополнение множества А до универсального множества У называется множество (символически А ), содержащее элементы универсального множества, не лежащие в А, т.е. А \ А. Наглядное изображение рис.5

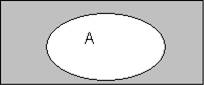
рис.5

Например: У- множество натуральных чисел, А={р р>7}, тогда А={ 4,5,6}. Определение 5. Разбиением множества А на непересекающиеся классы Al,A2, Ап называется множество подмножеств Al,A2, . . . Ап, если: 1) подмножества Al,A2, . . . Ап попарно не пересекаются

2) объединение всех подмножеств Al,A2, . Ап совпадает с множеством А.

Например: Разбиение множества студентов университета на группы.

Основные свойства операций:

1 операции объединения)

2.АаВ=ВпА(коммутативность операции пересечения)

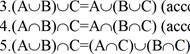(ассоциативность объединения)

(ассоциативность пересечения)

(дистрибутивность операции пересечения относительно операции объединения)

(дистрибутивность операции объединения относительно операции пересечения)

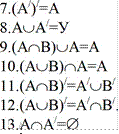
Определение Р(А)- множество всех подмножеств множества А называется Булеан множества А.

Тема 2. Упорядоченная пара, кортеж. Декартово произведение множеств и его свойства.

Определение 6. Упорядоченной парой называется двух-элементное множество {а,в} , для которого каким-то образом определен порядок следования элементов.

Символически          где а считается первой компонентой, а в второй.

Аналогично определяется понятие упорядоченной тройки упорядоченной п-ки ф1,а2,.. ее также называют кортежом длины п.

Два кортежа <al,a2,..        <Bl,B2,. .          называются равными (символически (аьа2,..

) тогда и только тогда, когда al-=Bl, и=в2,.. „ ап—Вп

Таким образом пары не равны, т.е.               (3,2)

Определение 7. Декартовым (прямым) произведением множеств А и В (символически А*В) называется множество всевозможных упорядоченных пар, у которых первая компонента из множества А, а вторая из множества В, т.е. аеА,в еВ} .

т.е.                          ,                     , тогда                                                                             <3,4>}.

Аналогично определяется декартово произведение трех и т.д. п множеств, т.е. al eAl,a2GA2,.. .,апеАп}

Если все Ai равны А, то Al *А2*...            обозначается А^П и называется п-ой степенью множества А. Примеры: 1 .если R множество действительных чисел, то R²- множество всевозможных пар действительных чисел. Множество R² можно изобразить множеством точек координатной плоскости, R - множеством точек трехмерного пространства.

2.Географические координаты точки земной поверхности: широта и долгота представляют элемент декартового произведения Ш *Д, где Ш=[-9О,9О], 180].

Вообще говоря

Тема З. Отношения и отображения на множествах. Виды отношений и отображений.

Определение 8. Отношением Р на множествах А и В называется любое подмножество РсА*В. Если            ер, то говорят элемент а связан с элементом отношением Р.

Областью определения отношения Р называется множество всех элементов множества А для которых существует элемент множества В с которым он связан этим отношением Р. Областью значений отношения Р называется множество всех элементов множества В для которых сутцествует элемент множества А с которым он связан отношением Р.

Множество всех пар       таких, что пара         ер называется обратным по отношению к Р и обозначается Р-1 (инверсией к Р).

Пусть Р с Х *У F с Y*Z. Композицией отношений Р и F называется отношение Р F с X*Z такое, что пара<хџ>е Р • F тогда и только тогда, когда существует у, такое, что пара <х,у> ер, а пара    eF.

Определение 9. Отношение FcA*B называется отображением А в В (символически F:

А—>В), если для любых аеА, Bl,B2GB из того, что E-F и E-F следует щ=в2. Если eF, то говорят элемент в образ элемента а, элемент а-прообраз элемента в при отображении Е

Отображение F: А—>В называется отображением А на В, если для любого в ев сутцествует аеА такой,             E-F.

Отображение F: А—>В называется одно-однозначным, если для любых al,a2GA и в ев из того, E-F и E-F следует м=а2. Отображение F: А—>В называется взаимно-однозначным, если F отображение А на В и взаимно-однозначное.

Пусть F: А—>В. Возьмем F-l cB*A. Понятно, что не всякое является отображением. Например: ,             ,           , ,         ,5>,<4,6>,<5,6>}.

Здесь отношение Fl не отображение,               eFl и (2,3) eF1.

F2 является отображением А в В, но не является отображением А на В. Инверсия к F2 отношение Ь- не является отображением.

F3 взаимно-однозначное отображение, т.к. оно одно-однозначное и отображение А на

в.

Пусть f: Х—>У, g:Y—>Z. Композицией отображений fII g называется отображение g • f : X—>Z такое, что  g • ћогда и только тогда, когда для некоторого у пара 4 и пара

Понятно, что операция • некоммутативная, но ассоциативная. Два множества А и В называются равномощными, если существует взаимно однозначное отображение F: А—>В. В этом случае пишут А — В и говорят мощность множества А равна мощности множества В. Если множество А содержит п элементов, то пиплуг А =n. Если множество А равномощно множеству натуральных чисел, то пишут А = о, т.е. первой бесконечной мощности. Эти и конечные множества называют счетными. Можно показать, что множество действительных чисел не равномощно множеству натуральных чисел, хотя и бесконечно. Множество равномощное множеству действительных чисел называют множеством мощности континуума, которое на данном этапе мы можем называть второй бесконечностью.

Например множество целых чисел равномощно множеству рациональных чисел, а также множеству натуральных чисел. Множество действительных чисел равномощно множеству иррациональных чисел, а также множеству всех подмножеств множества натуральных чисел.

Тема 4. Функции, операции на множествах, нейтральный и обратный элементы. Числовая функция, суперпозиция функций, обратная функция.

Отображение F: А—>В называется функцией, если существует общая процедура (алгоритм) получения (вычисления) для любого элемента аеА его образа в ев.

(Примерами вычислительных процедур могут считаться формулы, графики, таблицы.)

Функция F: называется п-местной операцией на множестве А. Если А множество функций, то употребляют термин оператор: примером может служить оператор дифференцирования функции. 2-х местная операция * называется коммутативной (перестановочной), если для любых элементов а,в Е-А выполняется а*в=в*а и называется ассоциативной, если для любых элементов а,в,с ЕА выполняется

(а*в)*с=а*(в*с). Операция * называется дистрибутивной (сочетательной) относительно операции • если для любых а,в,с из А выполняется (а•в)*с=(а*с)•(в*с).

Элемент а Е-А называется нейтральным справа относительно операции , если для любого в Е-А выполняется в*а=в и нейтральным слева, если а*в=в. Элемент называется нейтральным, если он нейтральный и справа и слева (иногда его называют единичным, как например для операции умножения - 1, или нулевым, как для операции сложения — О. В общем случае он обозначается через е.

Теорема. Если нейтральный элемент для операции существует, то он единственный для этой операции.

Примеры: В множестве ЬЦеЛЫХ чисел О является нейтральным элементом относительно сложения, а 1 нейтральным элементом относительно умножения.

Элемент a-l Е-А называется обратным справа для элемента аеА относительно операции , если выполняется а*а       обратный слева, если а        и просто обратным для а, если он обратный и справа и слева. Примеры: В множестве фрациональных чисел —3 обратный элемент для З относительно операции сложения, а — обратный элемент З

относительно операции умножения.

Определение 10. Функция F: А^П В называется числовой п-местной функцией, если А и В числовые множества. Символически F(xl,№,.. .,хп ). Суперпозиция (композиция) функции f: R—>R от функции g:R—>R является функция f(g):R—>R такая, что ef(g) тогда и только тогда, когда существует zeR такое, что ef(g) и ef(g). В общем случае f: от gl,g,. . . , где у: к <. Символически .,y). Класс элементарных функций есть множество всех суперпозиций так называемых основных элементарных функций (одноместных: степенных, показательных, логарифмических, тригонометрических, обратных тригонометрических и двухместных функций, представляющих арифметические операции). В суперпозиции функций могут измениться как сами переменные, так и их число.

Если обратное отношение F-l для F является функцией, то F-1 называется обратной функцией.

Формула — это выражение, описывающее суперпозицию и содержащее функциональные знаки, символы независимых переменных (аргументов) и констант (параметров). Формула с использованием скобок определяет порядок действий при вычислении. Функция f: Rⁿ        называется п-местной символически записывают   .

Метод определения объектов называется индуктивным, когда вводятся начальные объекты, и задается способ образования из них других, более сложных объектов. Функция, ставящее в соответствие элементам множества М значение единицу, а элементам дополнения множества М до универсального множества значение ноль называется характеристической функцией множества М.

Тема 5. Унарные, бинарные, тернарные, п-местные отношения на множестве.

Виды бинарных отношений.

Пусть А множество. Любое РсА^П называется п-местным (парным) отношением на множестве А. Если п=2, то Р называют бинарным (двухместным) отношением на А. Если n=l, то Р называют унарным (одноместным) отношением на А. Если ер, то говорят элемент а с элементом в находится в отношении Р и иногда записывают аРв или а=Р(в).

Примеры: 1) Отношение равенства двух чисел.

З) Отношение старшинства между людьми по возрасту или званию.

4) Родственные и другие отношения между людьми: «быть отцом», «быть внуком», «быть одноклассниками».

Обратное отношение Р-1 к отношению Р называют инверсией отношения Р.

Примеры: Инверсией к отношению «больше» является отношение «меньше», старше моложе, дороже —дешевле.

Отношение Р на множестве А называется:

1)      Рефлексивное (соответственно антирефлексивным), если для любого аеА, ер   ЕР).

2)      Симметричное, если для любых а,в еА, из того, что            ер следует      ер.

З) Антисимметричное, если для любых а,в еА, из того, что ер и ер следует а=в.

4)      Транзитивное, если для любых а,в,с еА, из того, что           ер и     ер следует

5)      Отношением эквивалентности, если оно одновременно рефлексивное, симметричное и транзитивное.

6)      Отношением порядка, если оно одновременно антисимметричное и транзитивное

7)      Отношением строгого порядка, если оно одновременно антирефлексивное, антисимметричное и транзитивное.

8)      Отношением нестрогого порядка, если оно одновременно рефлексивное, антисимметричное и транзитивное.

Примеры: Пусть А={          . Рассмотрим 4 отношения:

Р²={<а,а>,                       <а,с>,                       ;

Р <а,с>, <с,а>, . В таблице сведены свойства, кото ым довлетво яют эти соотношения:

	рефлексивно	антирефлексивно	симметрично	антисимметрично	транзитивно

Имеется связь между отношениями эквивалентности на множестве и разбиениями этого множества.

Теорема. Каждому отношению эквивалентности на множестве соответствует разбиение этого множества на непересекающиеся классы и обратно, каждому разбиению соответствует отношение эквивалентности.

Определение. Множество с заданным отношением порядка на нем называют упорядоченным множеством.

Множество А с отношением порядка Р называется

1)     Линейно-упорядоченным, если для любых а,в еА, а#в, выполняется одно из двух, либо           ер либо          ер.

2)     Дискретным, если для любого аеА либо существует веА такой, что не существует такого сеА, что       ер и     ер либо не существует такого веА, что     ер. З) Плотно-упорядоченным, если для любых       из А    ер, существует сеА, ер,     ер

4)      Элемент аеА называется максимальным (минимальным) по порядку Р, если не сутцествует веА, т.ч. ер ЕР). Таких элементов может существовать несколько.

5)      Элемент аеА называется наибольшим (наименьшим) в А по порядку Р, если для любого веА,       следует           ер        ЕР). Такой элемент может и не сутцествовать.

6)      Отношение Р называется вполне упорядоченным, если для любого МсА в М сутцествует наименьший элемент по порядку Р.

Примеры: 1) Отношение «равенства» является рефлексивным, симметричным, транзитивным и значит отношением эквивалентности

2)Отношение «больше», «меньше» являются антирефлексивными, антисимметричными, транзитивными.

З)Отношение «параллельности прямых» является рефлексивным, симметричным, транзитивным и значит отношением эквивалентности.

Пусть М-упорядоченное множество отношением порядка <. Элемент а называется минимальным (максимальным), если не существует в такого, что а (а< в). Элемент а называется наименьшим (наибольшим), если для любого в либо « в, либо а=в (либо а, либо а=в).

Понятно, если наименьший (наибольший) элемент существует, то он совпадает с минимальным (наибольшим).

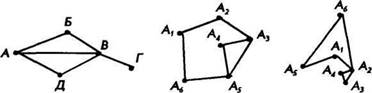
Пример упорядоченного множества, имеющего два минимальных элемента и ни одного наименьшего (рис. 6)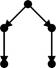

Рис.б

Тема 6. Алгераические структуры. Группы, кольца, поля. Изоморфизм алгебраических структур.

Мнжество М вместе с заданной на нем системой отношений и операций р

) называется алгебраической структурой, С) называется сигнатурой этой алгебраической структуры, а М — носителем, Кномер отношения, пј-местность отношения, ј-номер операции, тј-местность операции. Обозначение А= <М (Ь или <М, , 17 ^т) >. Если сигнатура содержит только операции, то такая алгебраическая

структура называется алгеброй.

Примерами алгебр могут быть группы, кольца, поля и т. д.

Группой называется алгебра <М *> где * - ассоциативная двуместная операция и:

1)      в М сутцествует нейтральный элемент е относительно операции

2)      для каждого элемента аеМ существует обратный элемент а- Е-М такой, что а*а-

—е.

Основное свойство группы то, что в ней всегда решаются уравнения а*х=в и х*а=в.

Решениями будут соответственно х=а ¹ и х=в*а ¹

Если операция * коммутативная, то группа называется абелевой.

Кольцом называется алгебра <М + *> такая, что <М +> является группой, операция дистрибутивна относительно операции +.

Если операция * ассоциативна, то кольцо называется ассоциативным.

Полем называется кольцо с нейтральным элементом относительно второй операции и для каждого не нейтрального элемента относительно первой операции из носителя сутцествует обратный элемент относительно второй операции.

Примеры. Пусть N- множество натуральных чисел, Z- множество целых чисел, Qмножество рациональных чисел, №множество действительных чисел + * -обычные числовые операции сложения и умножения, тогда:

1)      Алгебра <N, +>- не группа; <N, Ъ- не группа

2)      <Z +>- группа, <Z + *>- кольцо; <Z + *>- не поле

З) <Q +>-группа; <Q-{O}, Ъ- группа; <Q,+, * >- кольцо; <Q,+ Ъ- поле

4) <R, +> - группа;         0}, *> - группа; <R + *> - кольцо;а, + Ъ- поле. Пример алгебраической структуры:

Обычная арифметика натуральных чисел с отношением порядка < + * < >. Изоморфизм алгебраических структур.

Две алгебраические структуры МЕ <А, , тј > И < В, , > одинаковой сигнатуры называются изоморфными, если сулцествует взаимно ооднозначное соответствие Т: А—>В такое, что для любого отношения и соответствующего 71i для любых из Аи соответствующих T(al),... ,Цап) из В выполняется <

и для любой операции                  и

соответствующей операции R ^т и любых из А и соответствующих

из В выполняется <  е тт ^пг )—                  (

Подчеркнем, что изоморфизм - это не просто взаимно однозначное соответствие (его для конечных множеств - можно установить между любыми двумя множествами с одинаковым числом элементов). Смысл этого понятия состоит в том, что если выполнить в алгебре А какие-либо операции над определенными элементами мужества Ми соответствующие операции в алгебре В над соответствующими элементами множества Л^К , то результаты операций также будут соответствовать друг другу, то же самое относительно принадлежности кортежей соответствующим отношениям.

Тема 7. Комбинаторика. Правила суммы и произведения. Размещения, перестановки и сочетания.

Комбинаторная конфигурация- это расположение конечного множества элементов удовлетворяющее ряду специальных свойств. К основным комбинаторным конфигурациям относятся размещения, перестановки и сочетания.

Пусть п(А)-количество элементов множества А. Правило суммы: п(АиВ) =п(А) + п(В) - п(АаВ).

Правило произведения : п(А*В) =п(А)* п(В)

Для экономии места в компьютере и в тетради введем обозначение п! (читается пфакториал).

0! 1

1

Пусть М—конечное множество, состоящее из п элементов

Определение 1. Упорядоченное подмножество, состоящее из К- элементов множества М без повторений, называется размещением из п элементов по К без повторений О < К < п. Количество всех различных размещений без повторений из п элементов по К вычисляется по формуле

К

п (п- l)(n - 2)...(n - К)

Определение 2. Размещение из п элементов по п без повторений называется перестановкой. Количество всех различных перестановок из п элементов вычисляется по формуле

Определение З. Упорядоченное подмножество, состоящее из К- элементов множества М с повторениями, называется размещением из п элементов по К с повторениями О < К < п. Количество всех различных размещений с повторениями из п элементов по К вычисляется по формуле АпК = ПК

Определение 4. Подмножество, состоящее из К элементов множества М О<К<п называется сочетанием из п элементов по К. Количество всех различных сочетаний из п элементов по К вычисляется по формуле

                                  К!                          К!(п — К)!

Теорема 4: с ^к = с ^{п к} (7) cn+l^{k l} = +Cn^k (8)

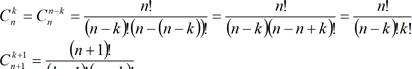
(к + 1)! (11 — к)!

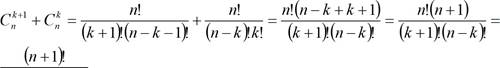
(к + 1)! (11 — к)!

/8/ формула доказана. Мы применили эти равенства:

54. Операции над двоичными числами

Каждому с детства привычен способ записи чисел в десятичной системе. Эта система называется позиционной десятичной, потому что натуральное число представляется словом в алфавите из десяти арабских цифр цк) =[0,l,2,3,...,9], причем знаки числа изображают различные его составляющие в зависимости от разряда - позиции в числе и служат коэффициентами при степенях 10. Например,

48087 = 40000 +8000 +80 + 7 = 4*10⁴ + +7*10⁰ и цифра 8 во втором разряде изображает число 80, а та же цифра в четвертом разряде - число 8000. Позиционная система исторически вытеснила другие способы представления чисел благодаря удобствам использования, главным образом, из-за достаточно простых арифметических действий над многозначными числами. Таким же образом , только много проще , устроена двоичная система счисления. Числа представляются словами в алфавите Например  вот

двоичное представление нескольких первых натуральных чисел (в левом столбце- десятичные; в правом- двоичные):

         0-0                      2- 10                  4 — 100   5 - 101      6- 110

7 - lll 8- 1000 9 -lOOl -lOlO П - lOll - ПОО 13— 1101 и т.д. Подобно тому, как в десятичнои системе счисления целые степени основания 10 записываются единицей с нулями, а число на меньшее- 99...9, в двоичной системе счисления число 10...0 с к нулями изображает число У, а число . из к единиц равно 2^k-l

Таблица сложения для двоичных чисел чрезвычайно проста: О + О = 0• 0+1 = 1+0 = 1 + 1 = 10. Таблица умножения еще проще:

          0х0 = 0х1 = 1х0 = О; 1х1   1.

Их можно представить и таблицами с двумя входами:

0

0

Отсюда - простота деиствии над многозначными числами, хотя двоичная запись числа длиннее десятичной более, чем втрое. Предыдущий пример демонстрирует перевод двоичного числа в десятичное. Для этого, так же как и для обратного перехода полезно знать значения целых степенеи числа 2: 1, 2, 4, 8, 16, 32, 64, 128, 256

512, 1024 и т.д. Например, 179 = 128 + 51 = 2 ⁷ +32 + 19 27 +25 З = 27 +25 + 24 +2 + поэтому двоичная запись числа

179 - 10110011 (слагаемые      входят в сумму 179 с коэффициентом 0, остальные степени 2-с коэффициентом 1). Ниже -примеры арифметических действий над двоичными числами (параллельно приведены действия с теми же числами в десятичной записи).

1010=8+2 х   х 101011 =32+8+2+l—-43 lOlOOlO = 64+16+2 82           lOlO lOlO.            40 1010...             430

1010...

llOlOlllO 256+ 128+32+8+4+2=430

1101=16+8+4+1

11001=16+8+1

Как видим, сложение, вычитание и умножение многозначных двоичных чисел производится так же, как и для десятичных, в частности, в обеих системах К-й знак результата арифметических действий зависит от К-х знаков слагаемых/сомножителей и знаков младших разрядов. Однако накопление знаков переноса при сложении возникает здесь значительно чаще: каждые две единицы дают перенос одной единицы в следующий - старший - разряд, сложение четырех единиц дает две единицы переноса, т.е. перенос одной единицы на два разряда влево.

Деление двоичных чисел ”столбиком” также намного проще, чем в десятичной системе, поскольку не приходится подбирать очередной знак частного: остаток не должен быть меньше делителя, - в этом случае знак частного ; в противном случае, как и для десятичных чисел он равен 0, и нужно приписать к остатку (снести) очередной разряд делимого.

Тема 8. Алгебра высказываний. Формулы. Законы логики. Равносильные формулы.

Релейно контактные схемы.

Алгебра высказываний. Высказывания и операции над ними.

Высказывание — связанное повествовательное предложение, о котором можно сказать истинно оно или ложно.

Примеры: «2х2=4»; <<2<3»; «Астана- столица Казахстана» - истинные высказывания. «2>5»; «Астана — столица России» - ложные высказывания.

«Ты пойдешь в университет?»; «Слава Карагандинским шахтерам!»; «х+З=5»; не являются высказываниями.

В дальнейшем нас интересует не то, о чем идет речь в высказывании ( его содержательная часть), а лишь какое значение истинности («истинна» или «ложь») оно имеет.

Операции над высказываниями.

Отрицание- унарная логическая операция, соответствующая конструкциям: «Не... », «Не верно, что.. .». Символически ПА

Конъюнкция (логическое умножение) -соответствует союзу «и» в русском языке, т.е. конструкции «... и.. .». Символически АлВ.

Дизъюнкция (логическое сложение) соответствует неразделительному «или», т.е. конструкции «... или.. .». Символически AvB.

Импликация соответствует конструкции «Если.. „ то.. .». Символически А—>В Эквиваленция (равносильность) соответствует конструкции «.. .тогда и только тогда, когда.. .». Символически АеВ.

Таблицы истинности для этих операций:

	в		АлВ	АМВ
и	и	л	и	и	и	и
и	л	л	л	и	л	л
л	и	и	л	и	и	л
л	л	и	л	л	и	и

Введенные операции не являются независимыми, одни из них могут быть выражены через другие. Два высказывания А и В будем называть равносильными (символически А=В), если

А=и сэ В=и.

Примеры равносильностей: 1.

                 2.        (ПА) А -закон двойного отрицания

З. AvB BvA • АлВ=ВлА; -законы коммутативности для и л

4.                                                                                                -законы ассоциативности для v и л -законы

дистрибутивности соответственно v относительно л, и л относительно м.

6.                                          AvA=A • АлА=А; —законы идемпотентности

7.                                          —законы де ЛЛоргана

8.                                          Avl 1; Ало О; AvO А; Ал 1 А; - законы нуля и единицы

9.                                          Ам(АлВ) А; Ал(АмВ) А; - законы поглощения

10.                                      1; - закон исключения третьего

11.                                      О — закон противоречия

Дадим определение формулы алгебры высказываний.

Пусть сутцествует некоторое множество элементарных высказываний (типа «2>3 которые будем обозначать первыми буквами латинского алфавита, а также 0,1. Введем в рассмотрение высказывательные переменные — символы, вместо которых можно подставлять высказывания, которые, как правило, обозначают последними буквами латинского алфавита (Х, У Z Т W,.. .). Введем также знаки логических операций и два символа «(«- открывающая скобка и «)»-закрывающая скобка.

Определение формулы дадим индуктивно т.е. определяются простые, а затем как из простых получать более сложные формулы:

1.     Элементарные высказывания, символы логических переменных формулы

2.     Если хи Т -формулы, то (пх), (ХАТ), (XvT), (ХЭТ), (ХЭТ) - формулы З. Других формул нет.

Примем соглашение об упрощении записи формул:

1. наружные скобки в записи формул можно опускать;

2. установим приоритет операций —я, л,м, —», е, т. е. сильнее л и т. д. Для каждой формулы F( Х... У), зависящей от высказывательных переменных Х... У можно дать ее полную таблицу истинности.

П име : Р xy,z = — ХАУ -»Z

х			ХАУ	(ХАУ)
и	и	и	и	л	и
и	и	л	и	л	и
и	л	и	л	и	и
л	и	и	л	и	и
и	л	л	л	и	л
л	и	л	л	и	л
л	л	и	л	и	и
л	л	л	л	и	л

Если формула зависит от п высказывательных переменных, то различных наборов будет уже У.

Формулы Fl (Xl,X2,.. .,Хп) и F2(Xl,X2,... ,Хп) называются равносильными, если их таблицы истинности совпадают (Символически Fl (Х1,Х2,.. .,Хп) F2(Xl,X2,... ,Хп) Формула называется тавтологией или законом логики, если в ее таблице истинности последний столбец полностью состоит из значений «истина». Примеры тавтологий: 1. Av—A —закон исключения третьего

1.      (А —» В) —» („В —» „А) —закон контропозиции

2.      (—А—>(В л  -закон метода отпротивного

Формула называется противоречием, если ее последний столбец в таблице истинности полностью состоит из значений «ложь». Например:

Тема 9. ДНФ и КНФ. Булева алгебра. Полные системы логических функций. Введенные операции не являются независимыми, одни из них могут быть выражены через другие.

Выше мы рассматривали связки —я,

Система связок называется полной, если через них можно выразить остальные.

Например система {—,v} является полной, т.к. А—>В —AvB• АлВ= —(—Av—B);

           Аналогично, система {—,л} - полная, также              -полная, а например система

- не полная.

Никакая из вышеприведенных связок одна не может давать полную систему. Но Шеффер и Пирс привели примеры связок, которые в единственном числе дают полную систему ( -штрих Шеффера, Т-стрелка Пирса), т.е. { }-ПОлиЯ, {Т} -полная. Таблицы истинности этих связок выглядят следующим образом:

	в	АТв
и	и	л	л
и	л	л	и
л	и	л	и
л	л	и	и

            Действительно :(АТВ) Т (АТВ) и            -полная следует, что

26

{ Т}- полная. Аналогично доказывается, что { }- полная.

В дальнейшем значение «истина» будем обозначать через 1, а значение «ложь» через 0.

Функция  называется булевой, если ее область определения и область значений является множество{0;1}. Мы уже знаем, что с каждой формулой алгебры высказываний связана такая функция. Но и для каждой булевой функции  можно построить формулу алгебры высказываний, таблица истинности которой совпадает с таблицей значений функции для соответствующих наборов значений переменных. Покажем это.

Будем говорить, что формула является элементарной конъюнкцией, если она есть конъюнкция простых высказываний или их отрицаний и каждое простое высказывание встречается в формуле только один раз. Возьмем определенный набор значений простых высказываний и эти высказывания, если они «истины(т.е. значение 1)», и с отрицанием, если они «ложны (т.е. значение 0)» соединим конъюнкциями. Полученную формулу назовем « элементарной конъюнкцией, соответствующей данному набору». Теперь для нашей функции образуем элементарные конъюнкции, соответствующие наборам, в которых функция принимает значения 1 и соединим их дизъюнкциями. Нетрудно проверить, что таблица истинности построенной формулы совпадает с таблицей значений нашей функции Теперь и для каждой формулы мы можем через ее таблицу истинности построить этим методом равносильную формулу, которая будет дизъюнкцией ее элементарных конъюнкций. В этом случае говорят, что формулу приводят к, СДНФ(совершенная дизъюнктивная нормальная форма).и СКНФ (совершенная конъюнктивная нормальная форма). Релейно-контактные схемы и схемы из функциональных элементов

Рассмотрим электромагнитные реле, состоящие из катушки индуктивности, контактнои группы и вспомогательных элементов (пружина, корпус и т. п.). Реле бывают двух типов; нормальноразомкнутые (рис.7) и нормально-замкнутые (рис. 8).

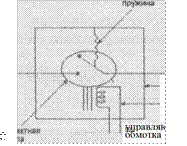
корпус

катушка

индуктивности

                                                                 Рис. 7                                                                       Рис.8

Условимся, что если по катушке индуктивности течет ток, то значение управляющего сигнала равно 1, если нет тока, то значение управляющего сигнала равно 0. Есгш контактная группа находится в замкнутом положении, то значение функции проводимости реле равно 1, если в разомкнутом — 0. Работа реле описывается таблицами:

Управ, сигнал Функция проводимости норм.-разомкн. реле 0 0

Управ, сигнал Функция проводимости норм.-замкн. реле 0 0

т. е. нормально-разомкнутое реле имеет тождественную функцию проводимости, а нормально-замкнутое отрицание управляющего сигнала. Если управляющий сигнал обозначить Х, то нормально-разомкнутое реле будем обозначать

х

нормально-замкнутое:

Рассмотрим схему:

Очевидно, ее функция проводимости - Ул—Х, т. е. последовательное соединение реле реализует конъюнкцию. Рассмотрим схему:

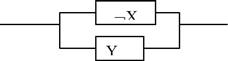
Очевидно, ее функция проводимости - Хм—У, т. е. параллельное соединение реле реализует дизъюнкцию.

                 Для краткости в дальнейшем переобозначим л - через        а v -через +

Определение Функцией проводимости схемы называется способность проводить или не проводить ток через схему соединения контактных групп реле в зависимости от комбинации управляющих сигналов, поданной на обмотки всех реле, образующих схему.

Сформулируем основные задачи теории релейно-контактных схем.

1.         Задача синтеза. Построить схему, реализующую заданную функцию проводимости.

Эта задача разрешима — достаточно построить формулу алгебры высказываний типа СДНФ или СКНФ (очевидно, что формулы такого типа реализуемы схемами).

2.         Задача упрощения. По данной схеме построить более простую схему, имеющую такую же функцию проводимости (равносильную схему).

Сразу заметим, что единого критерия простоты схемы нет, а пример упрощения будет приведен позже (машина голосования).

З. Задача анализа схемы. Не включая схему в работу, проанализировав соединения контактных групп, найти функцию проводимости схемы.

(Задачи такого типа — одна из составляющих промышленного шпионажа.)

В качестве примера решения задач 1 и 2 рассмотрим построение машины голосования.

Пример. Комитет состоит из трех человек (х, у, z) и принимает решения простым большинством голосов. Построить схему машины голосования для этого комитета так, чтобы в случае принятия решения загоралась лампочка.

Очевидно, если договориться о том, что в случае голосования «За» управляющий сигнал равен 1 а «Против» — 0, то функция проводимости имеет следующий вид:

х	О	О	О	о			1	1
	О	о		1	О		1	1
	о	1	о	1	о	1	о	1
Функция проводимости	О	О	о	1	о		1	1

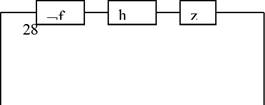
Выпишем по таблице СДНФ

          (—f)hz +           +             fhz , учитывая приоритет и оставшиеся скобки можно опустить.

Задача синтеза уже решена.

Нарисуем схему для полученной формулы:

				11			7,
				11
				11			7,

Перейдем к задаче упрощения (—nf)hz + + fhz (—f)hz + Пи + fhz+ +fhz (—f+f)hz + hz + fz + fh Нарисуем схему полученной формулы.

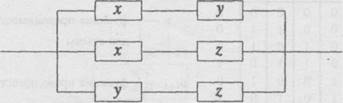
                       Мы сэкономили 6 реле (!). Можно продолжить упрощения hz + fz +             f(h+z)+hz

Сэкономлено еще одно реле но схема стала менее технологичной (потеряна симметричность). Нарисуем схему ддя полученной формулы

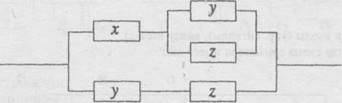
Двоичный сумматор

Перейдем к построению схемы основного элемента арифметического процессора любой ЭВМ — п-разрядного двоичного сумматора. п-разрядный сумматор будем строить из п штук одноразрядных двоичных сумматоров.

Управляющими сигналами одноразрядного сумматора i-m разряда являются ы, у значения Рго разряда слагаемых и - перенос в i-ii разряд из предыдущего (Pl = 0). В результате работы сумматора должны быть сформированы: а -значимые суммы в Ром разряде и Pi+l - значение переноса в i+l разряд.

Ясно, что работа сумматора описывается таблицей

О О о о 1 1 1 1	О о 1 1 О о 1 1	О 1 о 1 о 1 О 1	О 1 1 О 1 О О 1	О 1 1 1 1

- функция

проводимости для суммы

Pi+ - функция проводимости для переноса

Очевидно, Pi+l= v vypi (см. машину голосования). а— —Pi+1(Xi у v р) v xiYil)i.

Построим схему одноразрядного сумматора как схему из функциональных элементов, используя такие элементы:

                                                    дизъюнюдия•,конъюнкция                                 отрицание

(вверху входы (упр. сигналы), внизу выход).

Тогда схема сумматора имеет вид:

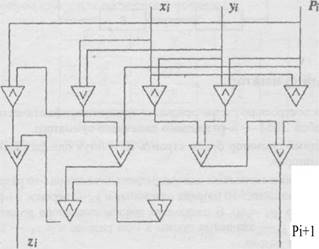
Релеино-контактные схемы и схемы из функциональных элементов

Полученную схему одноразрядного сумматора можем считать функциональным элементом с тремя входами и двумя выходами.

	м	у		Pi

Pi+1 Т

Построим теперь схему п-разрядного сумматора:

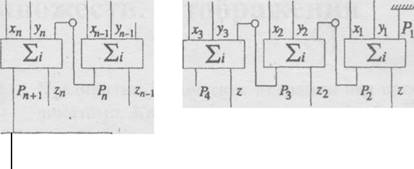                  Рз             2

на устройство управления машины

О — элементы задержки, запирающие сумматор до того, как прошло суммирование в предыдуцем разряде. РП+1 подается на устройство управления для выработки сигнала о переполнении сумматора в случае, когда pn+l = 1. Вход заземлен.

Тема 10. Основные принципы формализации аксиоматической теории. Исчисление высказываний. Теоремы о дедукции и о полноте.

Представление некоторой содержательной теории в виде формальной позволяет выявить общие свойства, полезные аналогии и ответить на ряд общих вопросов. Формализация процесса правильных рассуждений достигается с помощью аксиоматизации. Формальная аксиоматическая теория Т (формальная система, исчисление) задается следующим образом:

1.      Алфавит А символов, называемых символами теории. Слова в алфавите А называются выражениями теории Т.

2.      Выделено некоторое подмножество множества выражений, называемых формулами теории Т (правильно построенные выражения)

З. Выделено некоторое подмножество множества формул, называемых аксиомами теории Т.

4.      Имеется конечное множество правил вывода R1,.. .,Rm , каждое из которых есть отношение между формулами. Если А1,.. .,Ак В — фоормулы и выполнено <Al,.. .,Ак B>GRi , то В называется непосредственным следствием формул А1,.. .,Ак , полученным по правилу Ri.

5.      Выводом (доказательством) в теории Т называется всякая последовательность (кортеж) формул АБ.. „Ак такая, что для i=1 2,.. формула Ai есть либо аксиома теории Т, либо непосредственное следствие каких либо предыдущих формул этой последовательности. Формула С называется теоремой теории Т, если существует вывод, в котором последней формулой является С (символически т (Такой вывод формулы С может быть не единственным в теории Т). Таким образам, теоремы теории - это формулы, которые могут быть выведены из аксиом по принятым правилам.

В более общем смысле, можно рассматривать вывод не только из аксиом. Пусть Г={ Al,.. .,Ак } множество формул, назовем их гипотезами. Будем говорить, что формула F выводится из гипотез множества Г (символически Г Е), если существует последовательность формул Cl,.. „Ср, F, каждая из которых есть либо аксиома, либо принадлежит множеству Г, либо есть непосредственное следствие из предыдуцих формул вывода, а Cl,.. „Ср, F называется выводом формулы F из множества гипотез Г.

Частный случай, когда ГО, т.е. F есть следствие только аксиом (символически Е). Некоторые свойства выводимости:

2. ЕслиГ РА, тог,в НА

З. ЕслиГ Р Аи Г  Нс, тог Нс

4. Если {Al,...Ap, В} [— С и  ЕВ, то  [—С

Теория Т называется полной, если для любой формулы А выполняется обязательно выполняется ли60 ТА, либо КТ ПА .

Теория Т называется непротиворечивой, если ни для какой формулы А не должны быть выводимы в теории Т обе формулы А и ПА.

Исчисление высказываний (ИВ).

Один из возможных способов формализации логики высказываний- построение исчисления высказываний в виде формальной аксиоматической теории.

1.      Алфавит ИВ:

-символы переменных Х У ... Xi

ЛОГИЧеСКИХ СИМВОЛа —1 - правая и левая скобки ( , );

2.      Формулы ИВ:

а) все переменные

б) если А, В — формулы, то (ПА), А—>В) - формулы

Для сокращения и упрощения записи будем опускать внешние скобки в формулах, а также пары скобок, без которых можно восстановить порядок действий, соблюдая следующую договоренность: знак относится к кратчайшей подформуле, следующей за этим знаком. Также введем следующие сокращения —» —В) ;

Также как в алгебре высказываний введем приоритет на л, м,

З. Аксиомы ИВ : (Каждое из этих выражений представляют собственно не сами аксиомы они называются схемами аксиом, так как вместо А В С в них могут быть подставлены любые формулы)

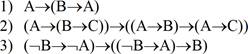
4.      Единственное правило вывода- силлогизм modus ponens , который обычно записывается в виде А, А—>В ^Р В (т.е. формула В есть непосредственное следствие формул А и А—>В.

5.      Понятия доказательства и теорема такие же как сформулированные при введении основных принципов формализации теории.

Важное свойство в формальном исчислении высказываний составляет

Теорема о дедукции. Если Г, А ^Е В то Г

(Понятно, что слово теорема, здесь приведено как слово метаязыка).

Следствие (правило силлогизма). А—>В, В—>С

Следующая теорема устанавливает связь между алгеброй высказываний (АВ) и исчислением высказываний (ИВ).

Теорема(полноте). Формула АВ - тавтология тогда и только тогда, когда она теорема ИВ.

Следствие. ИВ непротиворечиво.

Можно также ставить вопрос о независимости системы аксиом, т. е. О возможности или невозможности вывести одну из аксиом из остальных. Можно доказать, что расмотренная нами система аксиом, является независимой.

Тема 11. Алгебра и исчисление предикатов. Выполнимость, общезначимость форм, теоремы теории.

Повествовательное предложение, содержащее переменные так, что после подстановки вместо переменных имен объектов, оно превращается в высказывание, называется предикатом. Если переменных п, то этот предикат называется п-местным предикатом. Например: х>з; х+у=5; Х — столица Казахстана. Если мы теперь, например подставим в двуместный предикат вместо х 2, а вместо у З, то получим 2+3=5 истинное высказывание, а если подставим в место х 4. а вместо у 7, то получим 4+7=5 — ложное высказывание. Поятно, что у каждого предиката имеется множество определенности т.е. множество объектов где он имеет смысл. Так, например, если в предикат х >З вместо х подставить Кокшетав, то получим Кокшетав >З, предложение не имеющее смысла, а если подставим в предикат Х столица Казахстана, то получим высказывание Кокшетав — столица Казахстана. Т.е. высказывание, имеющее смысл, но ложное высказывание.

Каждому предикату Р соответствует множество истинности предиката Ip т.е. множество элементов на которых он истинен и множество ложности предиката Lp, т.е. множество элементов на которых он ложен. Таким образом множество определенности предиката разбивается на два подмножества: множество истинности и множество ложности предиката. Если P(al, для некоторых элементов, то это означает, что <M,.. т.е. под пместным предикатом понимается некоторое п-местное отношение на множестве определенности предиката (интерпретация предиката).

Введем операции над предикатами —я, с теми же названиями, что и в алгебре высказываний. По определению пусть: I = Ip IQ •, IpvQ -Ip • Ipe.>Q = Ip П IQ U „р П —Q .

Предикаты P(Xl, ,хп) И Q(Xl, ,хп) называются равносильными, если IQ (символически P(Xl, ,хп) Q(Xl

Множество предикатов с операциями образуют булеву алгебру, т.е. для них справедливы те же 1 1 равносильности, что и приведенные в алгебре высказываний.

Введем также операции, уменьшающие местность предиката:

1.      фиксация значений переменной

2.      навешивание кванторов (квантификация)

Пусть P(Xl, ,хп). Придадим переменной Xi некоторое значение s, тогда говорят, что предикат

Q(Xl, хп) P(Xl хп) получен из предиката Р(м,.. хп) фиксацией значения переменной Xi—S.

Пусть Р(х)-предикат. Выражение Ух Р(х) читается «для любого х выполняется Р(х)» и означает, что Ух Р(х) =l (т.е. истинно) тогда и только тогда, когда при подстановке вместо переменной х любого элемента из области определенности предиката Р(х) образуется истинное высказывание.

Выражение 3х Р(х) читается «сутцествует х для которого выполняется Р(х)» и означает, что 3х P(x)=l (т.е. истинно) тогда и только тогда, когда в области определенности предиката Р(х) существует элемент такой, что при подстановке его вместо переменной х образуется истинное высказывание.

Операция навешивания кванторов применяется и к многоместным предикатам. Пусть

P(Xl,  ,Xi-l,Xi,Xi+l,... хп)- п-местный предикат. Выражения     Р(Х1   Xi-1 Xi Xi+l

3Xi P(Xl, хп) это уже п- 1 -местные предикаты, в этих предикатах Xi называется связанной, а м, хп- свободными переменными.

Пример. Пусть Р(х,у) = «у для действительных чисел x,yeR . Это 2-местный предикат с предметной областью на числовой плоскости. Область истинности полуплоскость, ограниченная биссектрисой I и III координатных углов, включающая точки границы (на рис.9 показано штриховкой). Формулы

Ух Р(х,у) и Уу Р(х,у)- одноместные предикаты со свободными переменными у и, соответственно, х . Область истинности - пустое множество, так как не существует ни наибольшего, ни наименьшего среди действительных чисел. Предикат 3х Р(х,у) одноместный со свободной переменной у. Его область истинности - вся числовая ось так как какое бы ни было у , существует меньшее число х

Рассмотрим тот же предикат Р(х,у) = х S у на предметной области натуральных чисел: x,yeN = {0,1,2,...}. Область истинности предиката-целочисленные точки I координатного угла, включая точки оси абсцис, расположенные над биссектрисой и на ней (на рис. показано выделенными точками). Область истинности для хпредиката Ух Р(х,у) — пустое множество, а для Уу Р(Х,У) область истинности состоит из одного числа О.

Отсюда можно заключить, что предикат

Вх (Уу Р(х,у)) есть истинное высказывание (обе

переменных - связанные), поскольку существует наименьшее натуральное число -

О.

Упражнение. Определите истинность следующих высказываний для х,уе

                                   ;                                      Зу

Примеры. 1) Для предиката Р(х,у) = х у формула Р(х,у)лР(у,х) выражает предикат х = у . Тот же предикат Р(х,у) может быть выражен через 3-местный предикат на множестве натуральных чисел Q(s,t,u) = (s +t =u) следующим образом:

Р(х,у) = 3s Q(s,x,y ), т.е. сутцествует такое s , что х +s=y , или у -х =s > О . Формула 3s:Q(s,s,

х) означает, что х - четное число (x=s+ s). Наконец, формула Р(х,у) х) выражает условие х < у .

2) предикат R(x,y,z} : «при делении на число Х дает остаток У» может быть выражен предикатной формулой ВК (x=kz+y), keN

Область истинности предиката, выраженного предикатной формулой, определяется областями истинности составляющих и применяемыми в формуле операциями.

Формулы алгебры предикатов (задаются индуктивно):

В формулах участвуют: х, у,... -символы предметных переменных; Р1(Х1,.. ,xnl), Р2

),.. .-символы предикатов; логические символы; У,В-символы кванторов

1.      Если Pi — пеместный предикатный символ,то Pi (м,.. ,xni)- формула; все ее переменные свободные.

2.      Если А-формула, то ПА тоже формула с теми же свободными и связанными

переменными.

З. Если А,В-формулы и нет переменных, свободных в одной из них и связанных в другой, то АЛВ AvB, А—>В, А<->В — тоже формулы с теми же свободными и

связанными переменными.

4. Если А-формула (не имеет переменную х в качестве связанной), то Ух А(х) и 3х А(х) тоже формулы, в которых переменная х становится связанной (ее может и       не быть вообще в формуле А), а другие переменные остаются такими же как в  формуле А.

Для удаления лишних скобок будем считать, что знак квантора связывает сильнее, чем знак логической операции. Если мы пишем формулу А(Х1,.. ,хп), то это означает, что все свободные переменные находятся среди м, хп (обычно связанные переменные не упоминают в таком виде формулы). Формула называется замкнутой (предложением), если она не имеет свободных переменных.

Интерпретация — это сопоставление каждому предикатному символу определенного отношения. Вообще говоря, предикат имеет бесконечное множество интерпретаций. Вопервых, может быть бесконечной область определенности предиката, и предикатному символу можно сопоставить бесконечное множество различных отношений. Во- вторых, предикат можно рассматривать на различных множествах.

С точки зрения истинности для предикатных формул вводятся следующие понятия:

Замкнутая формула F называется выполнимой, если существует интерпретация, в которой F имеет истинное значение. Выполнимая формула называется тождественно истинной (общезначимой), если она истина в любой интерпретации. Понятно, что формула F тождественно истинная тогда и только тогда, когда —F не выполнимая. Формулы F и (Э называют равносильными (символически F=G), если они равносильны во всех интерпретациях, т.е. когда F <-> (Э — тождественно истинная формула.

Пример:Зх Р(х) и УР(х) равносильны на одноэлементном множестве, а на множестве, содержащем более одного элемента это уже не так.

Некоторые тождественно истинные формулы:

1. А(х) —А(х); —3х А(х) <-> Ух -лА(х) (законы Моргана для предикатов) 2. если формула В не содержит свободную переменную х и в формулах А и В нет переменных свободных в одной и связанной в другой, то

3х (А(х) л В) <-> 3х А(х) л В; Ух (А(х)лВ) <-> Ух А(х) л В; Вх (A(x)vB) <-> Вх А(х) В; Ух (A(x)vB) <-> Ух А(х) v В; и если у не входит в А, то Ух А(х) А(у); А(у) Вх А(х)

З. Законы коммутативности для одноименных кванторов: УхУу А(х,у) <-> УуУх А(х,у); 3х3у А(х,у) <-> ЗуВх А(х,у)

4. Ух (А(х)лВ(х)) <-> Ух В(х); 3х (A(x)vB(x)) е» Вх В(х). В то же время, формулы

Ух (A(x)vB(x)) А(х) v Ух В(х); 3х(А(х)лВ(х)) е»Вх А(х)лЗх В(х) тождественно истинными не являются. Почему? Приведите пример интерпретации, где она ложна.

Исчисление предикатов

Метод доказательства формул, содержащих переменные, путем непосредственной подстановки в них предметных констант называется методом интерпретаций, или методом моделей. Подстановка констант позволяет интерпретировать формулу как содержательное утверждение об элементах конкретного множества. Поэтому такой метод, апеллирующий к содержательному смыслу интерпретированной формулы называют семантическим, т.е. смысловым. Это удобно при доказательстве выполнимости формул или их неэквивалентности, поскольку и в том и в другом случае достаточно найти одну подходящую подстановку (интерпретацию).

Метод интерпретаций можно применять и для исследования истинности формул на конечных предметных областях, так как если область М конечна, то кванторы выражают конечные формулы логики высказываний.

В этом случае все кванторные формулы можно заменить естественным способом и получить формулы, содержащие только символы предикатов и логических операций, после чего проверить истинность можно конечным числом подстановок констант.

Для большинства же предметных областей доказательство тождественной истинности формул методом интерпретаций связано с большими трудностями. Поэтому применяется другой прием- аксиоматизация,

т.е. построение формальной системы и порождение исследуемых формул из аксиом с помощью процедур вывода.

Как и для исчисления высказываний, для предикатных формул построение исчисления проводится путем указания некоторой совокупности формул, которые называются аксиомами, и заданием правил вывода, позволяющих из общезначимых формул получать общезначимые.

Мы рассмотрим здесь аксиоматическую теорию, представляющую частный случай исчисления предикатов. Символы теории - те же, что в определении предикатных формул. Предикатные формулы определим так же, но в качестве логических символов будем использовать, как и в варианте исчисления высказывании, только два: , и —» (остальные можно ввести, применяя соответствующие эквивалентности для булевых функций).

Аксиомы исчисления предикатов.

Аксиомы А 1-А4 совпадают с такими же для исчисления высказываний.

А5. VXi P(Xi) —» P(Xl) , где формула P(Xi) не содержит переменной .

Аб. P(Xi) —» 3х1 P(Xl) с тем же условием, что и в А5.

Правила вывода ( при этом не должны нарушаться требования к правильности формул):  . Правило modus ponens:

в

2а. Правило связывания квантором:

где формула В не содержит переменной Xi

26. Правило связывания квантором В

В , где формула В не содержит переменной

З. Переименование связанной переменной: связанную переменную формулы А можно заменить в кванторе и во всех вхождениях в области деиствия квантора.

Понятия вывода, теоремы, вывода из системы гипотез определяются в исчислении предикатов так же, как в любой аксиоматической теории.

Приведем без доказательства несколько утверждений об исчислении предикатов (АД... - формулы в исчислении

Теорема 1. Если А В и существует вывод формулы В из формулы А , использующий только правило modus ponens, то Г (А—> В).

Теорема 2. Аксиомы исчисления предикатов — тождественно истинные формулы.

Теорема З. Формула, получаемая из тождественно истинной по любому правилу вывода 1-3, является тождественно истиннои.

Из двух последних теорем следует

Теорема 4. Любая выводимая в исчислении предикатов формула —тождественно истинна. Теорема 5. Исчисление предикатов непротиворечиво, так как в силу теоремы 4 невозможно вывести одновременно А и ПА .

Определенное выше исчисление предикатов называют узким исчислением предикатов, в отличие от не рассматриваемого нами расширенного исчисления, в котором допускаются кванторы не только по предметным переменным, но и по предикатным переменным.

Теорема 6 (Гёделя). В узком исчислении предикатов всякая тождественно истинная формула выводима.

Тема 12. Теория графов. Основные понятия и определения. Операции над графами. Числа графов Деревья, свойства деревьев

Первая работа по теории графов принадлежит Л. Эйлеру (1736 год), хотя термин «граф» впервые ввел в 1936 году венгерский математик Д.Кениг. Следующие шаги в развитии теории графов принадлежат Г.Кихгофу, применившему теорию графов в 1847г. к теории электрических цепей и А.Келли, раработавшему в 1857г. теорию деревьев и применившему ее к теории химических изомеров. Широкое дальнейшее приложение стала дополнительным стимулом ее бурного развития.

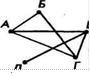
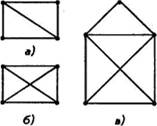
Графами были названы схемы, состоящие из точек и соединяющих эти точки отрезков прямых ш-ш кривых (примеры графов изображены на рисунке. 10 и 11).

                                                                           в

д

                                    д                                   а)                             б)

рис. 10 Нулевой граф с пятью вершинами                   рис. Неполные графы с пятью вершинами а), б)

С помощью графов часто упрощалось решение задач, сформулированных в различных областях знаний: в автоматике, электронике, физике, химии и др. С помощью графов изображаются схемы дорог, газопроводов, тепло- и электросети. Помогают графы в решении математических и экономических задач.

Евразийский национальный университет им. Л.Н. Гумилева

Учебно-методическии комплекс дисциплины

Издание: шестое

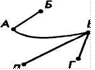
Познакомимся с основными понятиями теории графов при решении несложной задачи. Задача. Аркадий, Борис, Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано? Л Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени (рис. 10), а производимому рукопожатию отрезок или часть кривой, соединяющая конкретные точки имена (рис. 11). Точки А, Б, В, Г, Д называются вершинами графа, а отрезки линий (прямолинейные или криволинейные), соединяющие эти точки — ребрами графа.

Рассмотрим процесс соединения точек А, Б В, Г, Д ребрами.

1.                  Ситуация, соответствующая моменту, когда рукопожатия еще не совершались представляет собой точечную схему, изображенную на рисунке 2. Такая схема, состоящая из «изолированных» вершин, называется нулевым графом.

2.                  Ситуация, когда совершены еще не все рукопожатия, может схематически быть изображена, например,с помощью рисунка 1 1 а): пожали руки А и Б, А и В, В и Г, В ид. Следующий момент, когда добавятся, например, пожатия рук А я Г, Ги Б, может быть изображен графом на рисунке 116).

Графы, в которых не построены все возможные ребра (рис. 1 1 а), 6)), называются неполными графами.

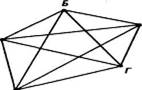
З. На рисунке 12 изображен граф, соответствующий всем совершенным рукопожатиям.

Этот граф является полным графом.

Если подсчитать число ребер графа, изображенного на рисунке 12, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми.

в

А

д

рис.12 Пшп--љй граф с пятью верп.пжал,ш

Их 10. А количество ребер в полном графе с п вершинами определяется как число неупорядоченных пар, составленных из всех п точек-ребер графа, т. е. как число сочетаний из п элементов по 2:

(7²11 = пф - 1)

Граф, не являющийся полным, можно дополнить до полного с теми же вершинами добавив недостающие ребра. Так, например, на рисунке 1 За) изображен неполный граф с пятью вершинами; обозначим его Т. Проведем другим цветом (или пунктирными линиями) ребра, превращающие граф Т в полный граф (рис. 136)).

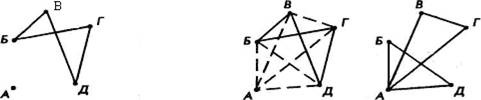в

           а)                                                                        в)

Евразийский национальный университет им. Л.Н. Гумилева

Учебно-методическии комплекс дисциплины

Издание: шестое

т

рис.1З

а) Неполный граф Т с пятью вершинами; 6) Пунктирными линиями изображено дополнение графа Т до полного графа; в) Граф Д — дополнение графа Т до полного на рисунке 136) или сплошными линиями на рисунке 1 Зв), называемый дополнением графа Т, который обозначается Т

S 2. Степень вершины

Количество ребер графа, исходящих из вершины, называют степенью этой вершины. На рисунке 14 изображен граф с пятью вершинами. Степень вершины А обозначим Ст. А. На рисунке 14: Ст. А = 1, Ст. Б = 2, Ст. В З, Ст. Г— 2, Ст. Д О.

Вершина называется нечетной, если степень этой вершины нечетная, четной если степень этой вершины четная.

Сформулируем некоторые закономерности, присущие определенным графам.

Закономерность 1. Степени вершин полного графа одинаковы, и каждая из них на 1 меньше числа вершин этого графа.

                                   рис.14                                                                рис.15

Пшп--љЙ граф с пятью верп.пжи,ш. Степени верп.п•ж потного

Ст.А=1,  ст.в=з, ст.д=п

графа ощжаковы и ра.вкљх п-1 (в дал--жом случае п=Э.

А Эта закономерность очевидна уже после рассмотрения любого полного.графа (см., например, полный граф с пятью вершинами на рис. 15); каждая вершина соединена ребром с каждой вершиной, кроме самой себя, т. е. из каждой вершины графа, имеющего л вершин, исходит л - 1 ребро. А

Если степени всех вершин графа равны, то граф называется однородным. Таким образом, любой полный граф — однородный.

Закономерность 2. Сумма степеней вершин графа число четное, равное удвоенному числу ребер графа.

Эта закономерность справедлива не только для полного, но и для любого графа.

А Действительно, каждое ребро графа связывает две вершины. Значит, если будем складывать число степеней всех вершин графа, то получим удвоенное число ребер 2R (R — число ребер графа), т. к. каждое ребро было подсчитано дважды.

Закономерность З. Число нечетных вершин любого графа четно.

Рассмотрим произвольный граф Г. Пусть в этом графе число вершин, степень которых 1, равна К1, число вершин, степень которых 2, равно Кх число вершин, степень которых п, равно Кп. Тогда сумму степеней вершин этого графа можно записать как Ю + 2К2 + ЗКз + ... + пКп.

С другой стороны: если число ребер графа R, то из закономерности 2 известно, что сумма степеней всех вершин графа равна 2R. Тогда можно записать равенство k1 +2k2+3k3+ ... +nkn=2R. (1)

Евразийский национальный университет им. Л.Н. Гумилева

Учебно-методическии комплекс дисциплины

Издание: шестое

Пусть Х —число нечетных вершин графа. Выделим в левой части равенства сумму, равную сумме всех нечетных степеней вершин графа К] + Кз+ ...=2Т+Х К1 + 2К2 + ЗКз + 4k4 + 5К5 + ... + пКп = 2Д= 2К+2Т+Х. Из этого равенства следует, что число

Х должно быть четным или равно нулю

Кенигсбергские мосты

Задача о кенигсбергских мостах.

К XVIII веку через реку, на которой стоял город Кенигсберг, было построено 7 мостов, которые связывали с берегами и друг с другом два острова, расположенные в пределах города (рис. 16).

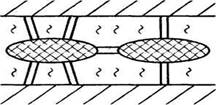
рис. 16

Задача заключается в следующем: нужно пройти (если это возможно) по всем семи мостам так, чтобы на каждом из них побывать лишь по одному разу и вернуться к тому месту, откуда начал маршрут.

Решить эту задачу удалось в 1736 г. Леонарду Эйлеру. В ходе решения задачи (после интерпретации условия задачи в виде графа, представленного на рисунке 17). Л. Эйлер установил следующие, помимо уже, рассмотренных нами, закономерности (которые мы примем без доказательства):

Закономерность 4 (вытекает из рассмотренной нами закономерности З). Невозможно начертить граф с нечетным числом нечетных вершин.

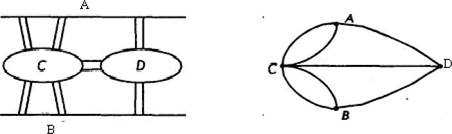
рис. 17

Ситуация с кенигсбергскими мостами и ее изображение в виде графа, где вершинами являются берега (А и В) и острова (С и D), а ребрами — мосты

Закономерность 5. Если все вершины граф четные, то можно не отрывая карандаш от бумаги («одним росчерком»), проводя по каждому ребру только один раз, начертить этот граф. Движение можно начать с любой вершины и закончить его в той же вершине.

Закономерность 6. Граф, имеющий всего две нечетные вершины, можно начертить, не отрывая карандаш от бумаги, при этом движение нужно начать с одной из этих нечетных вершин и закончить во второй из них.

Закономерность 7. Граф, имеющий более двух нечетных вершин, невозможно начертить «одним росчерком ».

Примем на веру сформулированные здесь свойства графов и вернемся к задаче о кенигсбергских мостах.

Евразийский национальный университет им. Л.Н. Гумилева

Учебно-методическии комплекс дисциплины

Издание: шестое

Прохождение по всем мостам при условии, что нужно на каждом побывать один раз и вернуться в точку начала путешествия, на языке теории графов выглядит как задача изображения «одним росчерком» графа, представленного на рисунке 17. Но, поскольку граф на рис. 17 имеет четыре нечетные вершины, то, согласно закономерности 7, такой граф начертить «одним росчерком» невозможно. Значит, и пройти по кенигсбергским мостам, соблюдая заданные условия, нельзя.

Графы, которые можно начертить одним росчерком на рис. 18

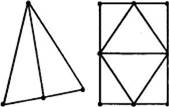
                                       г)                           д)

рис- 12

                РК. 18 а)                                                    рис. 18 б)

Путь в графе. Цикл

На рисунке 19 с помощью графа изображена схема дорог между населенными пунктами.

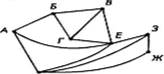
д

19

Например, из пункта А (вершина графа) в пункт З можно добраться различными маршрутами: АДЖЗ, АЕ3, АЕГВЕЗ, АБ-ВЕЗ и др.

Чем отличается маршрут АЕЗ от маршрута АЕГВЕЗ? Тем, что во втором маршруте на «перекрестке» в точке Е мы побывали дважды. Этот маршрут длиннее, чем АЕЗ.

Определение 1. Путем в графе от одной вершины к другой называется такая последовательность ребер, по которой можно проложить маршрут между этими вершинами. При этом никакое ребро маршрута не должно встречаться более одного раза.

Евразийский национальный университет им. Л.Н. Гумилева

Учебно-методическии комплекс дисциплины

Издание: шестое

Вершина, от которой проложен маршрут, называется началом пути, вершина в конце маршрута — конец пути.

Определение 2. Путь, в котором совпадают начало с концом, называется циклом.

Если все вершины цикла разные, то такой цикл называется элементарным (или простым) циклом. Если же цикл включает в себя все ребра графа по одному разу, то такой цикл называется Эйлеровой линией.

Так, на рисунке 18 циклами являются пути АДЕА, АДЖЗЕВБА, АДЕГВЕА и др., причем первые два названных     элементарные. На рисунке 18 приведены примеры Эйлеровых линий.

Очевидно, путь, проложенный по сторонам любого многоугольника, начинающийся и

заканчивающийся в одной и той же его вершине, является Эйлеровой линией. в

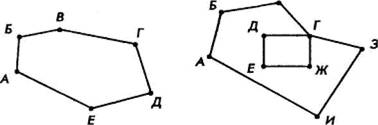
                                   а)                                                 б)

Примеры Эйдеровых линий

Леонард Эйлер (1707—1783 гг.) математик, механик, физик и астроном. Ученый необычайной широты интересов. Автор свыше 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближенным вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др., оказавших значительное влияние на развитие науки. Л. Эйлер по происхождению швейцарец. В 1726 г. был приглашен работать в Петербург, в 1727 г. переехал жить в Россию. В 1731 1741 и начиная с 1766 гг. был академиком Петербургской академии наук (в 1741 1766 гг. работал в Берлине, оставаясь почетным членом Петербургской академии наук).

Тема 12. Деревья, свойства деревьев

Определим более строго понятие графа. Ориентированным графом (Э называют тройку (X,U,f), где - множество, называемое множеством вершин графа, КЈ-множество (возможно и пустое), называемое множеством ребер, f: Х—>Х, называемое отображением инцидентности.

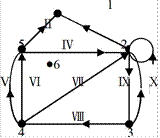Пример

Евразийский национальный университет им. Л.Н. Гумилева

Учебно-методическии комплекс дисциплины

Издание: шестое

                                                                                              ш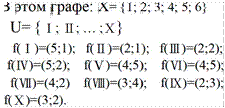                           

рис.21

Пусть ueU, f(u)=(x;y), то говорят, что ребро и инцидентна вершинам х и у. В дальнейшем под ребрами и, v,... будем сразу понимать им соответствующие пары (и), f(v),... Введем стандартные отображения: л(и)=х — начало ребра и, п(и)=у- конец ребра и. Ребра u,v называются параллельными (кратными), если f(u)=f(v), и противоположными, если f(u)=  Ребро и называется петлей в вершине х, если л(и)=п(и)=х. Вершина х называется изолированной, если для любого ueU выполняется и

Изоморфизм графов. Плоские и неплоские графы. Пути, цепи, контуры, циклы.

Определение. Графы Gl называются изоморфными

( символически Gl=G2), если сутцествуют взаимно однозначные отображения Ж: и џ: такие, что л(џ(и))=Цл(и)), п(џ(и))=Цп(и)).

Примеры графов Gl, 62 63, вернее их геометрическое изображение:

62 Рис.22	63
Имеем GkG2. Этот изоморфизм реализуют отображения	и О, заданные следующими
соотношениями: i(l)=2, i((2)=4, i(3)=l, i(4)=3 ; џ(	б ,          П

И м и м Понятно, что отношение изоморфизма на множестве графов рефлексивно, симметрично и транзитивно, т.е. это отношение эквивалентности.

Вообще, геометрическое изображение графа называется правильно реализованным, если его ребра не имеют общих точек, отличных от вершин графа. Понятно, что для любого графа существует его правильная реализация в R³ (трехмерное пространство).

Граф называется плоским (планарным), если у него существует его правильная реализация в R² (плоскость). Не все графы являются плоскими. Так например графы К5 и Кз,з (рис.2З) и графы, части которых устроены подобно им, не являются плоскими (теорема ПонтрягинаКуратовского).

гг                                        

кз,з

Рис.2З

Смысл и значения этого факта для микроэлектроники трудно переоценить. Фактически, из-за графов К5 и Кз,з пришлось создавать технологию многослойных печатных плат или микросхем в виде сэндвичей.

Евразийский национальный университет им. Л.Н. Гумилева

Учебно-методическии комплекс дисциплины

Издание: шестое

Путем длины п ( neN) на графе G(X,U,f) называется отображение такое, что п(џО- 1)) = л(џ(ђ), i = 2,3,.. .,n. Вершина называется началом пути, а вершина п(џ(п)) концом пути џ. Еслип(џ(п)), то путь называется контуром. Цепью длины п называется отображениеџ: [ 1

Тема. 13 Части графа: подграф, частичный граф. Связность и сильная связность, компоненты. Мосты графа

Части графа

В задачах теория графов иногда приходится изучать не весь граф в целом, а какие-то его части.

Определение Пусть G(X, [Г, Л) граф, U' С U- Частичным графом графа С;, лорожДеннььч (Л, назыаается граф Х, U',f

(ЗДесь                 ограничение  : U Х х Х на множество

U                 е- f : U' Х х Х по правилу

Пример. Пусть (G — схема дорог Ростовской области. Схема дорог Ростовской области с асфальтовым покрытием — частичный граф графа б.

Определение Пусть ЩХ, U, — граф, X^f ($ а) С Х. ПоДграфоеи графа С, порожДенным множествам Х называется граф

Пример . Схема дорог Багаевского района Акмолинской области - подграф схемы дорог Акмолинской области.

Сам граф (Э по отношению к своим подграфам и частичным графам называется надграфом (суграфом или суперграфом).

Компоненты связности и сильной связности

Определение           Пусть г вершина графа С(Х, f), Саяжеч с ней множество          опреДеленное слеДъ^јющим:

          у                 е. (у = т) V (существует цепь, ееДущая из х в у).

Евразийский национальный университет им. Л.Н. Гумилева

Учебно-методическии комплекс дисциплины

Издание: шестое

Теорема (свойства множеств (7$) Множества Сх облаДают слеДуюшщъш свойствами:

             (с, псу / а           4— су);

х ЕХ

 Нетрудно прхрить, Что отношение ат заданное следующим:

                хау                 (у х) (существует цепь, ведушдя из с в у),

является отношением эквивалентности на множестве Х — вершин графа. Действительно, его рефлективность очевидна, симметричность следует из лемпы об инвертировании цепи, а транзитивность следует из возможности склейки цепей, первая из которых заканчивается там, где начинается вторая.